지난 포스팅 https://studyingrabbit.tistory.com/81
중심력장 하에서 입자의 운동 (1) : 수치 미분 방정식 해법을 이용하여 문제 풀기 + 파이썬 시뮬레
지난 포스팅 https://studyingrabbit.tistory.com/79 [고전역학 문제 풀이] 원형 빗면(콘, 깔때기)에서 구르는 입자의 운동 고전역학에서는 꼭 배워야 하는 혹은 풀이법을 알아야 하는 문제(주제)들이 있는
studyingrabbit.tistory.com
에서 중심력장 하에서 입자의 운동에 대해서 알아 보았습니다. 대표적인 중심력장 문제라 할 수 있는 케플러 문제, 거리의 거듭 거듭 제곱에 비례하는 중심력장 문제, 단조화 진동자 문제 등에 대해서 알아 다루어 보았습니다. 이번 포스팅에서는 실제로 케플러 문제를 태양계에 적용하여 태양계 행성의 움직임을 시뮬레이션 해 보도록 하겠습니다.
실제 물리 상수 대입하기
지난 포스팅에서는 계산을 간단하게 하기 위해서 입자에 작용하는 힘을 $F = -\frac{1}{r^2} \hat{r}$ 과 같이 아주 간단하게 표현하였습니다. 그러나, 실제 태양-지구 문제를 풀기 위해서는 중력 상수, 태양의 질량, 지구의 질량과 같이 물리 상수를 대입하여 문제를 풀어야 합니다. 태양의 위치를 원점으로 했을 때, 지구에 작용하는 중력은
$$F_{earth} = -\frac{GM_{sun}m_{earth}}{r^2} \hat{r}$$ 가 됩니다. 여기서 $G$는 중력 상수, $M_{sum}$은 태양의 질량, $m_{earth}$은 지구의 질량 입니다. MKS 단위계를 사용하여 위 물리 상수들의 값을 나타내면
$$G = 6.673 \times 10^{-11} N m^2 kg^{-2}$$
$$M_{sum} = 1.988 \times 10^{30} kg$$
$$M_{earth} = 5.974 \times 10^{24} kg$$
이고, 이 값을 대입하면 지구의 운동 방정식은
$$5.974 \times 10^{24} \frac{d^2 \vec{r}}{dt^2} = - \frac{ 6.673 \times 10^{-11} \cdot 1.988 \times 10^{30} \cdot 5.974 \times 10^{24} }{r^2} \hat{r}$$
가 됩니다. MKS 단위계를 사용하였기 때문에 위 운동 방정식에서 거리의 단위는 당연히 미터 이고, 시간의 단위는 당연히 초 입니다.
실제 코딩에서 위 숫자를 직접 하나 하나 사용하여 코딩을 할 수 도 있으나, 매우 귀찮습니다. 계산 중간 중간에서 말 그대로 천문학적으로 매우 큰 숫자 혹은 그 반대로 매우 작은 숫자가 나올 수 있기 때문에 계산의 오차가 발생할 수 도 있습니다. 그리고 무엇 보다도 지구의 운동에서 우리에게 익숙한 공간과 시간의 스케일은 미터나 초가 아니라 천문 단위($AU$, 태양과 지구 사이의 거리) 와 년(지구가 태양을 한 번 공전하는데 걸리는 시간) 입니다. 따라서 계산을 하기 전에 최종적으로 우리가 풀어야 하는 방정식을 적절한 단위계를 선정하여 표현한다면, 계산을 쉽게 할 수 도 있고, 계산의 결과를 쉽게 이해할 수 있습니다.
단위계에 따른 운동 방정식의 변화
단위계에 따라서 우리가 수치적으로 풀어야 하는 운동 방정식의 최종 형태는 바뀌게 됩니다. 물론 시간에 따른 이계 미분방정식이라는 형식은 바뀌지 않고, 변수에 앞에 붙는 숫자의 크기가 달라집니다. 예를 들어, 시간의 단위를 $t_0$, 거리의 단위를 $r_0$, 질량의 단위를 $m_0$ 라고 하겠습니다. MTS 단위계 에서는 $t_0 = sec, r_0 = meter, m_0 = kg$ 이 됩니다. 이 단위계를 사용하여, 시간, 거리, 질량을 표현하면
$$t = t' t_0$$
$$r = r' r_0$$
$$m = m' m_0$$
이 됩니다. 여기서 $t', r', m'$ 는 단위가 없는 값만 나타내는 실수가 됩니다. 왜냐 하면, $t_0, r_0, m_0$가 단위를 의미 하기 때문입니다. 이 단위계를 사용하여 중력에 대한 운동 위 운동 방정식을 쓰면,
$$m_0 m' \frac{r_0}{t_0^2} \frac{d^2r'}{dt'^2} = \frac{GMm m_0^2}{r_0^2 r'^2}$$
이 됩니다. 위 식을 정리하면,
$$\frac{d^2 r'}{dt'^2} = \frac{t_0^2 GM}{r_0^3} \frac{1}{r'^2} = k\frac{1}{r'^2}, k = \frac{t_0^2 GM}{r_0^3} $$
이 됩니다. 여기서 $M$는 태양의 질량 입니다. $M' m_0$ 라고 써야하는게 맞지만, 굳이 그렇게 쓸 이유가 없어서 그냥 편의상 $M$으로만 표시하였습니다.
위 식에서 $k$로 표시한 상수와 단위들 곱과 나누기로 이루어진 값이 1이 된다면, 식은 매우 간단하게 표현 됩니다. 따라서, MKS 단위계를 쓰는 것 보다는 적절한 단위계를 잡아서, 즉 $m_0, r_0, t_0$ 값을 적절하게 잘 잡아서, $k$를 1로 만들어 주면, 문제가 매우 간단해 집니다. 그렇다면 어떠한 $m_0, r_0, t_0$ 값을 잡아야 할까요?
사람마다 "간단하다" 라고 느끼는 정도는 다 다르기 때문에 어떠한 단위계를 잡아야 하는지에 대한 답은 없습니다. 그러나 아마도 많은 사람이 생각하는 이 시스템에 꼭 맞게 어울리는 단위계는 앞에서도 미리 언급 한 것 처럼, $m_0$ 은 지구의 질량, $r_0$은 태양과 지구 사이의 거리, $t_0$는 지구의 공전 주기 나누기 $2 \pi$ 입니다. $t_0$의 단위를 지구의 공전 주기 그 자체로 하지 않고, 이 값을 $2 \pi$ 로 나눈 값을 사용하였는데, 나누기 $2 \pi$를 한 까닭은 지구의 공전 각속도 $\omega$를 1로 만들어 주기 위함 입니다. 이 경우 지구의 속도가 1이 되기 때문에 또한 편리합니다. 물론 $t_0$를 지구의 공전 주기 그 자체를 사용해도 됩니다.
$$r_0 = 1.48 \times 10^{11}km$$
$$t_0 = \frac{365.25 \times 86400}{2 \pi} sec$$
를 직접 대입하여 $k$ 값을 구하면, '우리가 원하는 대로 $k = 1.00$ 이 됩니다! (지구의 공전 궤도는 정확히 원이 아니라 타원이기 때문에 $k$ 값은 1.000000 은 아닙니다)
우리 문제에 매우 적절한 단위 계를 얻었기 때문에, 앞으로 모든 값들은 이 단위계로 쓰면 됩니다.
적절한 단위계를 다른 방식으로 유도해 보기
위에서는 아주 일반적인 방식으로 단위계에 따른 운동 방정식을 구하였고, 상수로 나오는 $k$를 1이 되게 하도록 단위계를 만들었습니다. 이렇게 해도 되지만, 우리가 고려하는 운동의 형태는 주로 등속 원운동 이기 때문에, 등속 원운동의 성질을 이용하여 보다 쉽게 적절한 단위계와 그에 따른 물리량의 변화를 구할 수 있습니다. 원운동에서 구심력 = 중력이라는 조건을 활용하면, 반지름이 $R$인 등속 원운동의 경우
$$\frac{mv^2}{R} = \frac{GMm}{R^2}$$
이 됩니다. 질량의 단위 $m_0$을 지구의 질량(이렇게 정의하면 $m =1$이 됩니다), 거리의 단위 $r_0$를 태양과 지구 사이의 거리(이렇게 정의하면 $R = 1$이 됩니다), 그리고 지구의 속도가 1이 되도록 시간 단위 $t_0$를 정한다면 위 식의 좌변은 1이 되고, 우변은 $GM$이 됩니다. 즉, 이 단위계에서는 중력 상수와 태양의 질량을 곱한 값이 1이 됩니다. 매우 귀찮은 값이던 $G$와 $M$이 사라지게 됩니다.
일반적으로 $R \ne 1$ 인 경우, $v = \sqrt{\frac{GM}{R}} = \frac{1}{\sqrt{R}}$ 로 매우 간단하게 원의 반지름에 따른 속도 $v$를 구할 수 있습니다. 예를 들어, 태양으로 부터 거리가 태양-지구 사이의 거리에 2배가 되는 지점에서 등속 원운동을 하는 행성이 있다면, 이 행성의 원운동의 속력은 지구의 속력의 $\frac{1}{\sqrt{2}}$ 배가 되는 것 입니다.
태양계 행성들의 움직임 계산하기
식을 최대한 간단히 하였으니, 이를 바탕으로 운동 방정식을 풀어서 태양계 행성들이 태양 주변을 공전하는 시뮬레이션을 해 보도록 하겠습니다. 한 번에 모든 행성의 움직임을 보면 조금 복잡하고 귀찮으니, 대표적으로 태양, 지구, 화성으로 이루어진 시스템만 고려하도록 하겠습니다. 태양의 질량은 지구와 화성의 질량에 비해서 훨씬 크기 때문에, 편의상 태양의 중심과, 전체 시스템의 질량 중심이 같다고 보도록 하겠습니다. 태양은 원점에 있고, 지구와 화성은 X축의 한 점에서 Y축 방향의 초속도를 갖는 등속 원운동을 한다고 가정하겠습니다. 태양-화성의 거리는 태양-지구의 거리의 약 1.523배 입니다. 우리 문제의 단위계를 활용하여 지구와 화성의 운동의 초기 위치와 속도를 표현하면
$$\vec{x}_{earth} = (1, 0), \vec{v}_{earth} = (0, 1)$$
$$\vec{x}_{mars} = (1.523, 0), \vec{v}_{mars} = (0, \frac{1}{\sqrt{1.523}})$$
이 됩니다. 이 초기 조건에 따른 운동 방정식을 계산하고 이를 애니메이션으로 나타내면 결과는 아래와 같습니다.
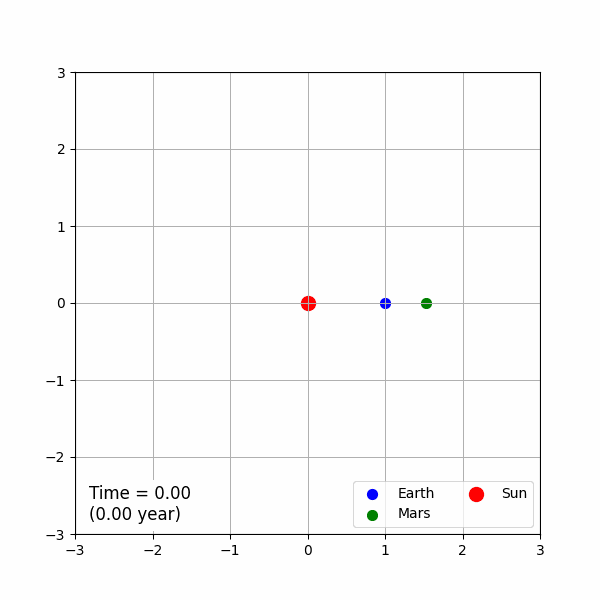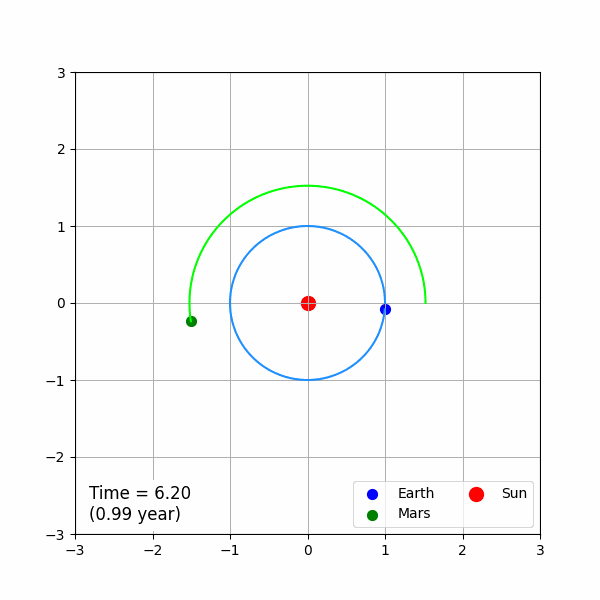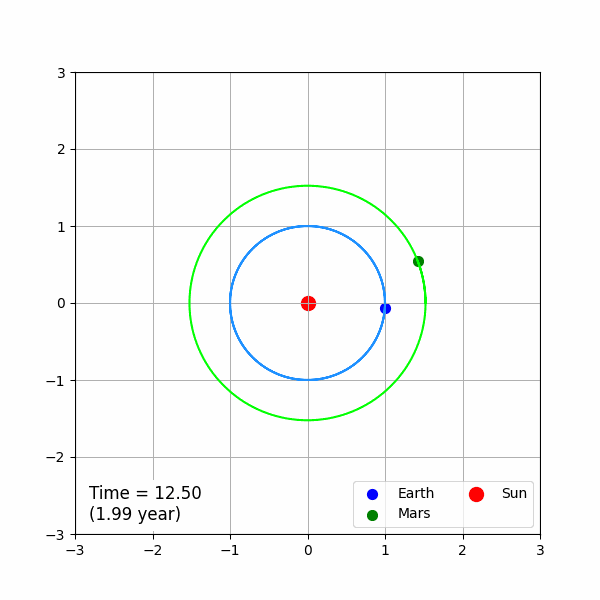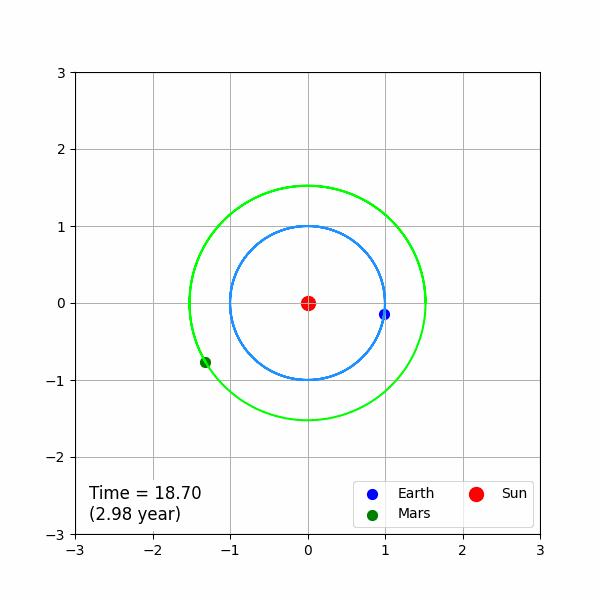
GIF 파일의 용량을 줄이기 위해서 전체 시뮬레이션 시간을 실제 물리 시간이 3년이 되도록 제한하였습니다. 그래프의 왼쪽 아래 Time이라고 하는 값은 문제에서 사용한 시간 단위를 기준으로 나타낸 시간이며, 이에 대응 하는 실제 물리 시간은 아래 괄호에 표현하였습니다. 파란색으로 표현한 지구는 정확히 물리 시간 1년에 한 번씩 태양 주위를 공전합니다. 화성의 실제 공전 주기는 1.88년인데, 시뮬레이션의 결과는 이에 부합 됩니다.
포스팅의 마지막 부분에 위 시뮬레이션의 파이썬 코드가 있으니, 파이썬 코딩을 할 줄 아는 분이라면, 지구와 화성 뿐 아니라 태양계의 다른 행성을 추가하여 시뮬레이션 해 볼 수 있습니다.
만일 화성의 질량이 매우 커진다면?
여기서 시뮬레이션을 그냥 마치면 심심하니, 물리 상수를 조금씩 변화시켜 가면서 행성 운동의 궤도가 어떻게 바뀌는지 알아 보도록 하겠습니다. 화성의 질량은 지구 질량에 비해서 매우 작은데, 만일 화성의 질량이 매우 커지면 어떻게 될까요? 아래 시뮬레이션은 화성의 질량이 지구이 질량의 10,000배가 된 경우의 행성의 궤적입니다.
지구의 질량의 10,000배라면 충분히 지구의 궤도에 영향을 줄 수 있는 수준입니다. 물론 태양의 질량 (지구의 질량의 약 300,000배)에는 여전히 $\frac{1}{30}$ 수준이지만, 지구와 화성의 거리가 가깝다면 화성으로 인한 지구 공전 궤도의 변화는 매우 클 것 입니다. 실제 시뮬레이션에서도 지구와 화성이 가까워 지는 시점에서 지구는 화성의 영향을 많이 받게 됩니다. 물론 그 전에도 화성의 영향으로 인해서 지구의 궤도는 원이 아니라 세차 운동을 하게 됩니다.
파이썬 코드
위 시뮬레이션을 하기 위해 만든 파이썬 코드 입니다. 적당히 코드의 내용을 수정해서 사용할 수 있습니다. 엄청 잘 만든 코드는 아니고 그냥 대충 편의상 빨리 만든 코드입니다.
import numpy as np
from matplotlib import pyplot as plt
from matplotlib import animation
plt.rcParams['animation.ffmpeg_path'] = 'C:\\Users\\jbae1\\Downloads\\ffmpeg-4.4.1-full_build\\bin\\ffmpeg'
def derivative(Z):
vel = velocity(Z)
acc = acceleration(Z)
ret = np.hstack([vel, acc])
return ret
def velocity(Z):
return Z[4:]
def acceleration(Z):
x1, y1, x2, y2 = Z[:4]
dx01 = x1
dy01 = y1
r01 = np.sqrt(dx01**2.0 + dy01**2.0)
f01_x = -G * m0 * m1 / r01**2 * (dx01 / r01)
f01_y = -G * m0 * m1 / r01**2 * (dy01 / r01)
dx02 = x2
dy02 = y2
r02 = np.sqrt(dx02**2.0 + dy02**2.0)
f02_x = -G * m0 * m2 / r02**2 * (dx02 / r02)
f02_y = -G * m0 * m2 / r02**2 * (dy02 / r02)
dx21 = x2 - x1
dy21 = y2 - y1
r21 = np.sqrt(dx21**2.0 + dy21**2.0)
f21_x = -G * m1 * m2 / r21**2 * (dx21 / r21)
f21_y = -G * m1 * m2 / r21**2 * (dy21 / r21)
f12_x = f21_x * (-1)
f12_y = f21_y * (-1)
ax1 = (f01_x + f12_x) / m1
ay1 = (f01_y + f12_y) / m1
ax2 = (f02_x + f21_x) / m2
ay2 = (f02_y + f21_y) / m2
return np.array([ax1, ay1, ax2, ay2])
def RK(Z, T):
### time interval ###
h = 0.001
N = int(T / h)
### initial ###
Z0 = np.array(Z)
TS = np.linspace(0, T, N+1)
list_Z = [Z0]
for t in TS[1:]:
print(t / T)
k1 = derivative(Z0)
k2 = derivative(Z0+h*k1/2)
k3 = derivative(Z0+h*k2/2)
k4 = derivative(Z0+h*k3)
Z1 = Z0 + h*(k1 + 2*k2 + 2*k3 + k4)/6
list_Z.append(Z1)
Z0 = np.array(Z1)
return TS, np.array(list_Z)
def update(num, Z, point1, line1, point2, line2, text, Nstep):
point1.set_offsets(Z[Nstep*num, :2])
line1.set_data(Z[:Nstep*num, 0], Z[:Nstep*num, 1])
point2.set_offsets(Z[Nstep*num, 2:4])
line2.set_data(Z[:Nstep*num, 2], Z[:Nstep*num, 3])
time = num*0.001*Nstep
time_year = time / (2*np.pi)
text.set_text("Time = {:0.2f}\n({:0.2f} year)".format(time, time_year))
if __name__ == '__main__':
Msun = 322_946
G = 1 / Msun
m0 = Msun
m1 = 1
m2 = 1
X = np.array([1, 0, 1.523, 0])
V = np.array([0, 1, 0, 1 / np.sqrt(1.523)])
Z = np.hstack([X, V])
T = 20 * (2*np.pi)
TS, list_Z = RK(Z, T)
##############
### figure ###
##############
Nstep = 100
#list_Z = list_Z[::Nstep]
fig = plt.figure(figsize=(6, 6))
ax = plt.axes()
ax.grid()
range = max([list_Z[:4].max(), -list_Z[:4].min()]) * 1.2
print(range)
range = 3
ax.set_xlim(-range, range)
ax.set_ylim(-range, range)
point1 = ax.scatter([], [], s=50, color='blue', label = 'Earth')
line1, = ax.plot([], [], color='dodgerblue')
point2 = ax.scatter([], [], s=50, color='green', label = 'Mars')
line2, = ax.plot([], [], color='lime')
ax.scatter([0], [0], s=100, color='red', label = 'Sun')
text = ax.text(0.03, 0.03, '', transform=ax.transAxes, fontsize='large')
text.set_bbox(dict(facecolor='white', alpha=1.0, edgecolor='white'))
plt.legend(loc = 'lower right', ncol = 2)
ani = animation.FuncAnimation(fig, update, len(TS) // Nstep, fargs=(list_Z, point1, line1, point2, line2, text, Nstep), interval=1, blit=False)
# ani.save('three_2.mp4', writer=animation.PillowWriter(fps=30))
# FFwriter = animation.FFMpegWriter(fps=30, extra_args=['-vcodec', 'libx264'])
# ani.save('three_2.mp4', writer=FFwriter, dpi=200)
plt.show()'물리학' 카테고리의 다른 글
| 여과percolation 이론을 컴퓨터를 이용하여 접근하기 (0) | 2023.05.11 |
|---|---|
| 시간에 따른 파동 함수의 변화 계산 하기 102 : 단조화 진동자와 결맞은 상태(coherent state) (0) | 2022.06.04 |
| 시간에 따른 파동 함수의 변화 계산 하기 101 : 상자 속 입자 문제와 1차원 스케터링 문제 (0) | 2022.06.01 |
| 렌즈, 물방울에 의한 빛의 굴절 : 공간에 따라 굴절률이 변하는 상황에서 Eikonal 방정식 풀기 + 신기루 현상 설명 (0) | 2022.04.17 |
| 빛의 진행 경로와 페르마의 원리와 Eikonal(아이코널) 방정식 : 페르마의 원리로 부터 스넬의 법칙 유도와 수치해법으로 문제 풀기(파이썬 코드) (1) | 2022.04.16 |



