페르마의 원리와 변분법
진공 공간에서 빛은 항상 일정한 속도 $c = 299,792,458m/s$로 직선으로 나아갑니다. 그러나 진공이 아닌 빛을 매개할 수 있는 물질 안에서 빛이 나아갈 경우, 반사와 굴절등으로 인해 빛의 속력과 방향은 시시각각 바뀌게 됩니다. 이 때, "과연 빛은 어떤 경로로 진행하는가?"에 대한 질문이 자연스럽게 생기게 되고, 1600년대를 살아간 프랑스의 변호사이자 수학자이자인 피에르 드 페르마(Pierre de Fermat)는 이에 대한 매우 간단하면서도 강력한 답변을 주었습니다.
페르마에 따르면, 빛이 $A$라는 위치 $x_A$에서 $B$라는 위치 $x_B$로 전파할 때, $x_A$와 $x_B$ 사이에서 빛이 진행하는 경로는 $x_A$에서 시작하여 $x_B$로 끝나는 모든 경로 중, 빛은 진행 시간이 가장 짧은 경로를 선택합니다. 굴절률이 $n \gt 1$인 물질에서 빛의 속도는 $v = \frac{c}{n}$로 줄어들게 됩니다. 굴절률이 크다면 속도가 줄어는 정도가 심하게 됩니다. 만일 $n=10$ 이라면 빛의 속도는 진공에서의 빛의 속도의 $\frac{1}{10}$이 됩니다. 따라서 임의의 위치 $x$에서 굴절률이 $n(x)$라고 한다면, 정확히 $x$라는 위치에서 빛의 속도는 $v = v(x) = \frac{c}{n(x)}$가 되고, 이 지점에서 $ds$만큼의 거리를 나아가는데 걸리는 시간은 $dt = \frac{ds}{v} = \frac{n(x)}{c}ds$가 됩니다. (3차원 공간상의) $x_A$에서 $x_B$를 잇는 경로(곡선 혹은 직선)을 하나 생각하여 이를 $c_{AB}$라고 한다면, 빛이 이 경로를 지나가는데 걸리는 시간은
$$T[c_{AB}] = \int_{c_{AB}} \frac{n(x)}{c}ds = \int_{c_{AB}} n(x)ds$$
가 됩니다. 두 번째 등호에서는 빛의 속도 $c$를 편의상 $1$로 두었습니다. 즉, 모든 속도는 빛의 속도를 기준으로 빛의 속도와의 비율로 생각할 수 있습니다. 위 적분은 3차원 공간에서의 선적분이 되는데, 경로 $c_{AB}$를 예를들면
$$x(t) \in \mathbb{R}^3, t \in [t_A, t_B], x(t_A) = x_A, x(t_B) = x_B$$
와 같이 매개변수화 했다고 하여 $t$에 대한 적분을 한다고 생각할 수 있습니다. 여기서 $ds$는 길이를 뜻 하는데, $x(t)$를 이용하여 표현하면, $\Big|\frac{dx}{dt}\Big| dt$ 라고 할 수 있습니다. 선적분에 대해서 익숙하신 분이라면 특별한 설명이 없더라도 위 식을 이해할 수 있을거라 생각합니다.
따라서, 페르마가 알려주는 빛이 경로는 $x_A$에서 $x_B$를 잇는 임의의 경로 중, 위에서 정의한 $T$를 가장 작게 만들어주는 경로가 됩니다. 이를 수학적으로 표현하면, $x_A$에서 $x_B$를 잇는 임의의 경로의 집합을 $C_{AB}$라고 할 때, 우리가 찾는 경로를 $c^*$라고 한다면,
$$c^* = \arg\min_{c \in C_{AB}} T[c]$$
이 됩니다. 여기서 $c$는 단순한 숫자(실수)가 아니라, 공간상에서 정의 된 함수이고, $T[c]$는 공간상에서 정의된 함수를 실수(시간)으로 바꾸어 주는 범함수이기 때문에, 이 문제는 매우 대표적이면서도 표준적인 변분법의 문제가 됩니다. 변분법에 맞게 위식을 바꿔서 표현하면
$$0 = \delta \int_{c} n(x)ds$$
인 $c$를 찾는 것이 문제입니다.
특수한 경우에 적용한 페르마의 원리 : 스넬의 굴절 법칙
3차원 공간상에서 매우 일반적으로 정의된 굴절률에 대해서 최단 시간 경로가 되는 경로 $c = c^*$를 찾는 것은 매우 어렵습니다. 해석적인 방법으로 풀리지 않을 수 있고, 따라서 수치적인 방법으로 풀어야 합니다. 하지만, 매우 특수한 형태의 $n(x)$에 대해서는 쉽게 해석적인 방법으로 $c^*$를 찾는 것이 가능합니다. 매우 간단한 경우인 3차원 공간에서 $n(x)$가
$$\begin{equation}
n(x, y, z)=\begin{cases}
n_A, &y \ge 0 \\
n_B, &y \lt 0
\end{cases}
\end{equation}$$
로 주어진 경우를 생각하겠습니다. 편의상 $n_B \gt n_A$로 놓겠습니다. $y=0$ 평면을 기준으로 위쪽은 $n(x,y,z) = n_A$이고, 아래 부분은 $n(x,y,z) = n_B$입니다. 또한 $x_A, x_B$는 $x_A = (x_A, y_A, z_0), x_B = (x_B, y_B, z_0)$로 놓도록 하겠습니다. $x_A$가 중복되어 사용되고 있긴 한데, 먼저 나온 $x_A$는 사실 $\vec{x}_A$로 받아들여야 합니다. $x_A$가 굴절률이 $n_A$인 물질 안에 위치한 점이고, $x_B$를 굴절률이 $n_B$인 물질안에 위치한 점이라고 생각하겠습니다. 즉, $y_A \gt 0, y_B \lt 0$입니다. 편의상, $x_A$와 $x_B$의 $z$ 좌표값은 같은 값으로 놓았습니다. 이 경우, 이 문제는 3차원 문제가 아니라 $X-Y$ 평면상에서 정의된 2차원 문제로 생각할 수 있습니다.

위에서 설명한 상황을 그림으로 그리면 위와 같습니다. 긴~ 설명이 그림 하나로 쉽게 설명이 됩니다. 이제 우리가 풀어야할 문제는 $x_A$와 $x_B$를 잇는 임의의 경로 중에서 $T[c]$를 최소로 하는 경로를 찾는 것 입니다. 임의의 경로를 생각하면 어렵습니다. 일단 임의의 경로라는 것을 어떻게 표현해야 하는지도 모르겠습니다. 따라서, 일단은 임의의 경로 집합 중에서 매우 특수한 경우인 두 선분으로 이루어진 경로를 정의하고, 이 경로에 대한 $T[c]$를 계산해 보도록 하겠습니다.

위 그림에서와 같이 경로 $c$를 $x_A \rightarrow x$를 잇는 선분(빨간색)과 $x \rightarrow x_B$를 잇는 선분(주황색)의 합으로 하겠습니다. 즉 $c = c_{AX} + c_{XB}$로 표현할 수 있습니다. 여기서 $x$는 위 그림에서 노란색으로 표시한 점 입니다. 이 점의 좌표는 $(x, 0)$이 됩니다. 역시나 $x$를 중복해서 사용하고 있는데, 노란색으로 표시한 점은 $\vec{x}$와 같이 벡터로 표현해야 합니다만 편의상 그냥 $x$로 표시하였습니다. 여기서 $x$의 값이 달라질 때 마다, 경로 $c$가 달라집니다. 따라서 경로 $c$를 $c(x)$로 표시할 수 있습니다.
이제 $T[c(x)]$를 한 번 계산해 보겠습니다. 우선 $T[c(x)] = T[c_{AX}] + T[c_{XB}]$ 인 것은 당연하고, $T[c_{AX}] = n_A |A -X|$ 가 됩니다. 즉 단순히 $c_{AX}$ 경로상의 굴절률 $n_A$과 $c_{AX}$의 길이 $|A-X|$의 곱으로 주어집니다. $|A-X| = \sqrt{(x_A - x)^2 + y_A^2}$ 이므로, (경로 $c_{XB}$에 대해서도 동일하게 계산하면)
$$T[c(x)] = T(x) = n_A \sqrt{(x_A - x)^2 + y_A^2} + n_B \sqrt{(x_B - x)^2 + y_B^2}$$
이 됩니다. $T$값은 경로 $c(x)$에 함수이지만, 경로 $c(x)$가 단순히 (실수값을 갖는) 변수 $x$에 의해 완전히 기술되기 때문에, $T[c(x)]$를 단순히 $x$의 함수 $T(x)$로 쓸 수 있습니다.
$T$에 대한 변분은 단순히 $T$에 대한 미분으로 바뀌게 되고, $\frac{dT}{dx} = 0$이 되게 하는 $x$가 우리가 찾는 $x^*$가 됩니다. 즉, $c = c_{Ax^*} + c_{x*B}$가 $x_A$에서 시작하여 $y=0$ 상의 점을 거쳐 $x_B$에 도착하는 두 선분으로 이루어진 경로 중에서, 빛이 전파되는데 가장 짧은 시간이 걸리는 경로가 되는 것 입니다. $x^*$는
$$\frac{dT}{dx} = n_A\frac{x_A- x^*}{\sqrt{(x_A - x^*)^2 + y_A^2}} + n_B\frac{x_B- x^*}{\sqrt{(x_B - x^*)^2 + y_B^2}} =0$$
를 만족해야하고, 식을 다시 정리하면, $x^*$는
$$n_A\frac{x^*-x_A}{\sqrt{(x_A - x^*)^2 + y_A^2}} = n_B\frac{x_B- x^*}{\sqrt{(x_B - x^*)^2 + y_B^2}}$$
를 만족하게 됩니다. 반대로 위 식을 성립하게 되는 $x^*$를 찾아야 합니다. 위 식의 양변을 제곱하고 통분을 하면 $x^*$에 대한 4차 방정식이 되고, 4차 방정식의 근의 공식을 이용하면 $x_A, y_A, x_B, y_B$에 대한 함수 $x^*$를 찾을 수 있습니다.
그렇게 해서 $x^*$를 찾을 수 있겠으나, 위 식의 기하학적 의미를 생각해 보도록 하겠습니다.

문제의 기하학적 형태에 위 수식에서 나온 분자, 분보의 값들을 표시하였습니다. 이로부터
$$\frac{x^*-x_A}{\sqrt{(x_A - x^*)^2 + y_A^2}} = \sin \theta_A$$
$$\frac{x_B- x^*}{\sqrt{(x_B - x^*)^2 + y_B^2}} = \sin \theta_B$$
가 됨을 확인 할 수 있고, 따라서 최단 경로의 조건을
$$n_A \sin \theta_A = n_B \sin \theta_B$$
로 표현할 수 있습니다. 이 식은 바로 굴절에 대한 스넬의 법칙(Snell's law) 입니다. 페르마의 원리에서 부터 시작하여 약간의 가정(즉, 경로는 두 선분의 합으로 이루어진다)을 하였더니 실제 물리 법칙인 스넬의 법칙을 얻은 것 입니다.
스넬의 굴절 법칙은 다양한 방법으로 유도할 수 있는데, 가장 물리적인(?) 방법은 맥스웰의 전자기 법칙(맥스웰 방정식)과 경계조건으로 부터 유도하는 것 입니다. 이는 순수하게 빛을 전자기파로 이해하고 전기와 자기의 성질로 부터 유도하는 것으로 물리학 전공 전자기학 과목의 2학기 수업에서 배우는 내용입니다. 또는 빛을 순수하게 파동으로 생각하여 호이겐스의 원리로 부터 유도하는 것인데, 개념적으로도 수학적으로도 가장 간단한 방법이라서 일반물리학에서는 이 방법으로 스넬의 법칙을 유도하는 것으로 알고 있습니다. 페르마의 원리는 맥스웰 방정식 보다 간단하고, 호이겐스의 원리 보다 일반적으로 사용될 수 있다는 면에서 매우 좋은 원리라 할 수 있습니다. 물리학에서는 이와 같이 한 가지 현상을 여러가지 법칙(원리)로 부터 이해(유도)할 수 있는 예시가 있는데, 스넬의 법칙은 매우 다양한 방법으로 유도될 수 있는 매우 구체적인 예 입니다.
우리가 찾은 해가 스넬의 법칙이니 문제를 제대로 풀었다고 만족할 수 있지만, 아직 하나 남은 간극을 채우지 못 했습니다. 문제를 간단히 하기 위해서 $x_A$에서 $x_B$로 가는 임의의 경로를 단순히 두 선분의 합으로 제한하고 문제를 풀었습니다. 즉, 임의의 경로에 대해서 문제를 풀지 않고, 특수한 경우에 대해서 문제를 푼 것 입니다. 그러나 이 문제는 쉽게 해결 될 수 있는데, $x_A$에서 시작하여 $x^*$가는 임의의 경로는 $x_A$와 $x^*$를 잇는 선분보다 길이가 길거나 같고, 따라서 임의의 경로에 대응되는 시간은 선분에 대응되는 시간 보다 항상 길거나 같습니다. 이 성질을 이용하면, 우리가 찾은 경로가 임의의 경로 중, 최적의 경로라는 것을 증명할 수 있습니다.
일반적인 빛의 경로를 알고 싶다면 : Eikonal 방정식
위에서 매우 특수한 형태의 굴절률이 배치 $n(x)$가 주어졌을 때, 빛의 경로를 구했습니다. 이번에는 매우 일반적인 $n(x)$가 주어졌을 때, 빛이 경로가 만족해야 하는 방정식을 찾아 보도록 하겠습니다. 이는 앞에서 언급한대로 $0 = \delta \int_{c} n(x)ds$ 를 만족하는 경로 $c$를 찾으면 됩니다. 이 문제는 $c(x)$에 대한 오일러-라그랑쥬 방정식을 풀면 됩니다. 여기서 $ds = \sqrt{\dot{x}^2 + \dot{y}^2 + \dot{z}^2}ds$로 쓸 수 있기 때문에(여기서 $\dot{x} = \frac{dx}{ds}$), 범함수는 $L = n(x,y,z)\sqrt{\dot{x}^2 + \dot{y}^2 + \dot{z}^2}$이 됩니다. $L$에 대한 오일러-라그랑쥬 방정식을 세우면,
$$\frac{d}{ds} \Big(n \frac{dx}{ds} \Big) = \frac{\partial n}{\partial x}$$
가 됩니다. $y, z$에 대해서도 동일한 식을 얻을 수 있습니다. 이 식을 Eikonal 방정식이라고 부릅니다. 굴절률이 공간의 위치에 따라 바뀌는 상황에서 빛의 경로를 알려주는 방정식 입니다.
"Eikonal" 이라는 단어의 한국어 번역 없습니다. 한국물리학회 물리학용어집에서 검색을 해도 단순히 음역인 "아이코널"을 사용합니다. 영문 위키피디아에 따르면 Eikonal은 그리스어에 근원을 두고 있으며 현대 영어로는 "image"를 뜻한다고 합니다. 즉, Eikonal 방정식은 "이미지 방정식"인데, 빛의 경로 이미지에 대한 방정식 정도로 생각하면 될 것 같습니다. 일문 위키피디아를 봐도 "アイコナール"(아이코나루)라고 단순 음역을 사용하고 있습니다. 중문 위키피디아를 보면, "程函方程"(정함방정)이라고 훈차를 하였습니다. 여기서 程(정)은 경로라는 뜻 입니다. 函(함)은 함수라는 뜻이고 方程(방정)은 방정식이라는 뜻 입니다. 즉 "경로에 대한 함수 방정식" 정도로 생각할 수 있습니다. 훈차를 한 것이라서 정확히는 "Eikonal"의 의미는 없는 것 같습니다.
Eikonal 방정식을 수치적인 방법으로 풀기
Eikonal 방정식은 $x$의 $s$에 대한 2계 미분방정식입니다. $s \rightarrow t$로 바꿔 놓는다면, 적어도 형식적으로는 Eikonal 방정식과 뉴턴의 운동 방정식은 같습니다. 따라서 뉴턴의 운동 방정식을 풀었을 때 처럼, 새로운 변수 $\dot{x}$를 도입하고 $x, \dot{x}$에 대한 연립 1계 미분 방정식을 풀면 됩니다. 위 Eikonal 방정식의 괄호 안에 있는 값을 $p$라고 정의하면,
$$\frac{dx}{ds} = \frac{p}{n}$$
$$\frac{dp}{ds} = \frac{\partial n}{\partial x} $$
가 얻어집니다. 입자의 운동 방정식과 비교하여 $p$를 운동량이라고 해석한다면, 첫 번째 식에서는 $n$이 질량과 같은 역할을 한다고 볼 수 있고, 두 번째 식에서는 $n$이 위치에너지(곱하기 -1)의 역할을 한다고 볼 수 있습니다. 초기 조건은 $$x(s=0) = x_0, p(s=0) = n \frac{dx}{ds}(s=0) = n\dot{x}(0)$$
으로 주어집니다.
이 미분 방정식은 시간 $t$로 자유도 $x, y$를 미분한 것이 아니라 곡선의 길이 $s$로 자유도 $x, y$를 미분한 것 입니다. 만일 파라미터가 $t$였다면, 시간에 따른 $x, y$의 움직임을 기술한 방정식이 될텐데, $s$이기 때문에 위 Eikonal 방정식은 길이 (빛이 공간상에서 나아간 거리)에 대한 $x, y$의 위치에 대한 방정식이 됩니다. 즉, 빛이 공간상에서 단위 길이 $\Delta s$만큼 나아갈 때, $x, y$ 방향으로 얼마나 나아간 거리 $\Delta x, \Delta y$를 알려주는 식입니다. $\Delta x, \Delta y, \Delta s$의 정의에 따라서 $\Delta s^2 = \Delta x^2 + \Delta y^2$ 이 됩니다.
초기 조건 $x(s=0)$은 빛의 초기 위치, $p(s=0) = n\dot{x}(s=0)$은 빛의 초기 진행 방향과 초기 위치에서 굴절률의 곱이 됩니다.
위 2변수의 1계 연립 미분방정식을 수치적으로 푸는 것은 이미 이전 포스팅에서 여러번 소개한 바 있기 때문에 구체적인 설명은 생략합니다. 이에 대해서 다룬 이전 포스팅을 보면 됩니다. 간단하게는 오일러 방법이나, 정확하게는 룽게-쿠타 방법을 활용하면 됩니다.
구체적인 굴절률과 초기 조건에 대해 문제 풀기
복잡한 문제를 풀기전에, 우리가 만든 수치해법 프로그램이 실제로 정확하게 작동하는지를 알아 보기 위해서, 해석적으로 답을 얻을 수 있는 문제를 풀어 보는 것이 좋습니다. 이 문제에 대해서 수치적인 방법으로 얻은 해와 해석적인 방법으로 얻은 해를 비교해 보면, 우리가 만든 수치해법 프로그램의 정확도를 확인할 수 있습니다.
해석적으로 푼 문제를 수치해법으로 다시 풀기
스넬의 법칙을 유도한 앞의 문제의 조건을 그대로 이용해 보겠습니다. 하지만, 위 문제의 공간에 따른 굴절률 $n(x, y) = n(y)$를 이용하기 위해서는 약간의 수정이 필요합니다. $n(y)$는 $y=0$에서 불연속함수인데, 따라서 $y=0$에서 $y$에 대한 미분이 불가능합니다. 이를 극복하기 위해서 불연속함수를 $\tanh$ 함수를 도입하여 표현할 것 입니다. 즉, $y \gt 0$에서 굴절률이 $n_1$ $y \lt 0$에서 굴절률이 $n_2$인 경우,
$$n(y) = \frac{n_1 - n_2}{2} \tanh \Big( \frac{y}{\sigma} \Big) + \frac{n_1 + n_2}{2}$$
로 근사할 것 입니다. 여기서 $\sigma$는 $y=0$ 주변에서 얼마나 가파르게 굴절률이 $n_1$에서 $n_2$로 변할 것인가를 기술하는 값인데 만일 $\sigma \rightarrow 0$이 되면 불연속한 함수가 됩니다. 수치해법 프로그램에서는 $\sigma$를 매우 작은 값으로 하되, 적당히 큰 값으로 해서 불연속으로 인해 생기는 문제를 적절하게 해결할 것 입니다.
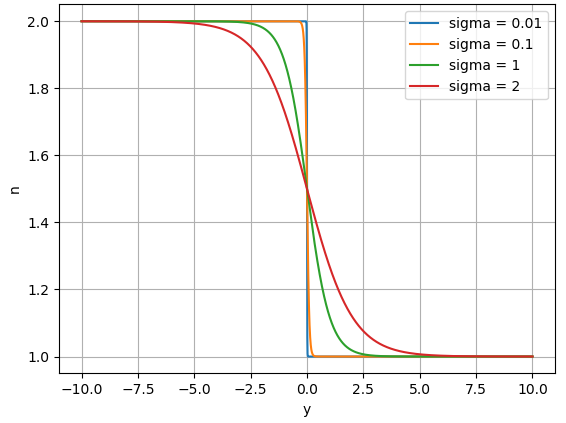
$\sigma = 0.01, 0.1, 1.0, 2.0$에 대한 굴절률 근사 함수의 개형은 위와 같습니다.

$n_1 = 1, n_2 = 2, \sigma = 0.1$ 의 조건에서 Eikonal 방정식을 풀어서 얻은 빛의 경로 입니다. 왼쪽 위 $(-10, 10)$의 위치에서 원점방향을 향해서 $n_1$ 영역에서 입사한 빛이 $n_2$ 영역으로 굴절되어 들어가는 경로의 해를 얻었습니다. 입사하는 빛의 각도가 $\frac{\pi}{4}$ 이므로, 스넬의 법칙에 따라 $y \lt 0$ 영역으로 굴절 돼 들어가는 빛의 입사 각도의 $\sin$ 값은 $\frac{1}{2\sqrt{2}} = 0.3535$가 되어야 합니다. 이 수치해법에서 얻은 입사각도의 $\sin$값은 $0.3516$ 으로 약 0.5% 정도 차이가 생깁니다. 이는 굴절률이 $y=0$에서 칼같이 $n_1 \rightarrow n_2$로 변하는 것이 아니라 $\sigma = 0.1$ 정도의 범위에서 천천히 변하기 때문에 생기는 현상입니다.
원점 근방을 확대하면

와 같습니다. 그림에서는 곡선을 그렸지만, 계산상에서 얻어지는 것은 위에서 표시한 점 입니다. 시각적 편의를 위해서 점과 점 사이를 선분으로 이은 것 입니다. 점과 점 사이의 거리는 $0.1$로 두고 계산하였습니다. 앞에서 언급한 이유 때문에, 빛는 원점 $(0,0)$에서 굴절하는 것이 아니라 그 전에 이미 굴절을 합니다.
$(-10, 10)$에서 다양한 방향으로 빛이 뿜어져 나아갔다고 하면, 다음과 같은 빛의 경로가 가능합니다.

반대로 빛이 $y \lt 0$의 한 점에서 시작하는 경우를 생각해 보겠습니다. 즉 굴절률이 큰 매질에서 굴절률이 작은 매질로 진행하는 경우 입니다.

$(-10, -10)$에서 시작한 빛이 다양한 입사각으로 굴절률 $n_2 = 2$인 매질에서 $n_1 = 1$인 매질로 진행합니다. 매우 재미난 현상을 발견할 수 있는데, 입사각이 0, 10, 20도 인 경우에는 $y \gt 0$ 영역으로 굴절하지만, 입사각이 30도 이상인 경우에는 $y \gt 0$ 영역으로 굴절하지 못 하고, $y=0$에서 반사하여, 다시 $y \lt 0$ 영역으로 돌아 옵니다. 이 현상은 바로 전반사 입니다.
전반사는 스넬의 법칙으로 부터 바로 유도할 수 있지만, 이처럼 보다 일반적인 경우를 가정하고 푼 Eikonal 방정식의 해로 부터도 전반사 해를 얻을 수 있습니다.

입사각도를 30도 근방에서 1도씩 변화 해 가면서 해를 얻었습니다. 입사각 29도까지는 굴절이 일어나지만, 30도 부터는 전반사가 일어납니다. 전반사의 임계각은 해석적으로 $\theta_c = \arcsin (\frac{n_1}{n_2}) = \arcsin(0.5) = \frac{\pi}{6}$, 즉 30도 입니다. 수치해법으로 부터 얻은 값과 동일합니다.
간단한 계산으로 부터 우리가 만든 수치해법 프로그램이 최소한 완전히 이상한 답을 주진 않은 다는 것을 확인하였습니다. 수치해법 프로그램으로는 임의의 굴절률 함수 $n(x, y)$에 대해서 빛의 경로를 구할 수 있으니, 다양한 $n(x,y)$에 대한 재미난 계산을 해 볼 수 있습니다.
다음 포스팅에서는 이번 포스팅에서 풀었던 매우 간단한 경우의 $n(x,y)$가 아닌 좀 더 복잡하고 재미난 굴절률 분포에 대한 빛의 진행을 게산해 보도록 하겠습니다.
아래는 이번 포스팅의 마지막 결과 그래프를 얻기 위해서 사용한 파이썬 코드 입니다. 예전에 만든 2계 미분 방정식을 푸는 룽게-쿠타 코드를 약간 변형한 것 입니다. 엄청 깔끔하게 만들어진 코드가 아니니, 파이썬 프로그래밍이 가능하다면, 핵심 부분만 참고하여 본인만의 프로그램을 만드는 것이 좋습니다. 아래 코드에서 velocity는 $\frac{dx}{ds}$를 뜻하고, acceleration은 $\frac{dp}{ds}$를 뜻 합니다.
import numpy as np
from matplotlib import pyplot as plt
def velocity_x(t, x, vx, y, vy):
n = index_refraction_type1(x,y, 'n')
return vx/n
def velocity_y(t, x, vx, y, vy):
n = index_refraction_type1(x, y, 'n')
return vy/n
def acceleration_x(t, x, vx, y, vy):
nx = index_refraction_type1(x,y, 'nx')
return nx
def acceleration_y(t, x, vx, y, vy):
ny = index_refraction_type1(x, y, 'ny')
return ny
def rungekutta_method(x0, y0, vx0, vy0, t0, t1, h):
N = int((t1 - t0) / h)
xs, vxs, ys, vys, ts = [x0], [vx0], [y0], [vy0], np.linspace(t0, t1, N)
for i in range(1, N):
t = t0 + h*(i-1)
k1x = velocity_x(t, x0, vx0, y0, vy0)
k1vx = acceleration_x(t, x0, vx0, y0, vy0)
k1y = velocity_y(t, x0, vx0, y0, vy0)
k1vy = acceleration_y(t, x0, vx0, y0, vy0)
k2x = velocity_x(t+h/2, x0+h*k1x/2, vx0+h*k1vx/2, y0+h*k1y/2, vy0+h*k1vy/2)
k2vx = acceleration_x(t+h/2, x0+h*k1x/2, vx0+h*k1vx/2, y0+h*k1y/2, vy0+h*k1vy/2)
k2y = velocity_y(t+h/2, x0+h*k1x/2, vx0+h*k1vx/2, y0+h*k1y/2, vy0+h*k1vy/2)
k2vy = acceleration_y(t+h/2, x0+h*k1x/2, vx0+h*k1vx/2, y0+h*k1y/2, vy0+h*k1vy/2)
k3x = velocity_x(t+h/2, x0+h*k2x/2, vx0+h*k2vx/2, y0+h*k2y/2, vy0+h*k2vy/2)
k3vx = acceleration_x(t+h/2, x0+h*k2x/2, vx0+h*k2vx/2, y0+h*k2y/2, vy0+h*k2vy/2)
k3y = velocity_y(t+h/2, x0+h*k2x/2, vx0+h*k2vx/2, y0+h*k2y/2, vy0+h*k2vy/2)
k3vy = acceleration_y(t+h/2, x0+h*k2x/2, vx0+h*k2vx/2, y0+h*k2y/2, vy0+h*k2vy/2)
k4x = velocity_x(t+h, x0+h*k3x, vx0+h*k3vx, y0+h*k3y, vy0+h*k3vy)
k4vx = acceleration_x(t+h, x0+h*k3x, vx0+h*k3vx, y0+h*k3y, vy0+h*k3vy)
k4y = velocity_y(t+h, x0+h*k3x, vx0+h*k3vx, y0+h*k3y, vy0+h*k3vy)
k4vy = acceleration_y(t+h, x0+h*k3x, vx0+h*k3vx, y0+h*k3y, vy0+h*k3vy)
x1 = x0 + h*(k1x + 2*k2x + 2*k3x + k4x)/6
vx1 = vx0 + h*(k1vx + 2*k2vx + 2*k3vx + k4vx)/6
y1 = y0 + h*(k1y + 2*k2y + 2*k3y + k4y)/6
vy1 = vy0 + h*(k1vy + 2*k2vy + 2*k3vy + k4vy)/6
xs.append(x1)
ys.append(y1)
vxs.append(vx1)
vys.append(vy1)
x0 = x1
y0 = y1
vx0 = vx1
vy0 = vy1
return np.array(ts), np.array(xs), np.array(ys), np.array(vxs), np.array(vys)
def index_refraction_type1(x, y, function):
n1, n2 = 1, 2
sigma = 0.01
A, B = (n1 - n2) / 2, (n1 + n2) / 2
if function == 'n':
n = A * np.tanh(y / sigma) + B
return n
elif function == 'nx':
nx = 0.0
return nx
elif function == 'ny':
ny = A / sigma * (1 - np.tanh(y / sigma) ** 2.0)
return ny
if __name__ == '__main__':
X0, Y0 = -10, -10
lim = 0.0
plt.figure(figsize=(8, 8))
for THETA_DEGREE in [57, 58, 59, 60, 61, 62, 63]:
THETA = np.pi/180 *THETA_DEGREE
VX0 = np.cos(THETA) * index_refraction_type1(X0, Y0, 'n')
VY0 = np.sin(THETA) * index_refraction_type1(X0, Y0, 'n')
T, X, Y, VX, VY = rungekutta_method(X0, Y0, VX0, VY0, 0.0, 30, 0.01)
lim = max(lim, max([X.max(), Y.max(), -X.min(), -Y.min()]))
plt.plot(X, Y, lw =2, label = "Angle = {}".format(90-THETA_DEGREE))
plt.scatter(X[0:1], Y[0:1], color ='black')
plt.axhline(0.0, color = 'black', lw = 1)
plt.xlim(-lim*1.05, lim*1.05)
plt.ylim(-lim*1.05, lim*1.05)
plt.xlabel('X')
plt.ylabel('Y')
plt.legend()
plt.grid()
plt.show()
'물리학' 카테고리의 다른 글
| 시간에 따른 파동 함수의 변화 계산 하기 101 : 상자 속 입자 문제와 1차원 스케터링 문제 (0) | 2022.06.01 |
|---|---|
| 렌즈, 물방울에 의한 빛의 굴절 : 공간에 따라 굴절률이 변하는 상황에서 Eikonal 방정식 풀기 + 신기루 현상 설명 (0) | 2022.04.17 |
| 중심력장 하에서 입자의 운동 (1) : 수치 미분 방정식 해법을 이용하여 문제 풀기 + 파이썬 시뮬레이션 코드 (0) | 2022.04.09 |
| 공전하는 두 천체가 만들어내는 평형점 : 라그랑주 점(Lagrange point) (1) | 2022.04.04 |
| [고전역학 문제 풀이] 원형 빗면(콘, 깔때기)에서 구르는 입자의 운동 (1) | 2022.04.01 |



