공전하는 두 천체가 만들어내는 평형점 : 라그랑주 점(Lagrange point)

천체물리학은 가장 역사가 깊은 과학의 분과 중 하나로, 뉴턴의 고전 역학의 정립 이후 큰 발전을 이루었습니다. 그 중에서 재미난 주제 중에 하나는 라그랑주 점(Lagrange point)인데, 라그랑주 점은 이를 발견한 프랑스의 수학자이자 물리학자인 조세프-루이르 라그랑주의 이름을 따서 불리고 있습니다. 

 

라그랑주 점은 공전(원운동)하는 두 큰 천체가 만들어 내는 힘의 평형점 입니다. 단순히 이렇게만 설명하면, 매우 어려운데 실제로 예를들어서 설명하면 더 쉽습니다. 태양-지구-위성으로 구성된 시스템을 생각하겠습니다. 태양은 지구에 비해 질량이 무척이나 크기 때문에, 사실상 태양은 원점에 고정 돼 있고, 지구는 태양 주변을 1년에 한 바퀴씩 공전하고 있습니다. 그리고 지구의 중력장에 의해서 속박 돼 있는 위성을 생각하도록 하겠습니다. 이 위성은 지구 주변을 공전하는 것 뿐 아니라 동시에 태양 주변을 공전하고 있습니다. 위성이 받는 힘은

 

(1)태양-위성의 중력,

(2)지구-위성의 중력, 그리고

(3)위성이 태양(원점) 주변을 공전하면서 받는 "원심력"

 

이 있습니다. 아시다 시피 원심력은 실제 힘은 아니지만, 뒤에서 설명할 논의에 따르면 "실제로 작용하는 힘" 처럼 생각할 수 있습니다. 따라서 위성이 받는 알짜힘은 $(1)+(2)+(3)$ 이 되고, 이 알짜힘이 0이 되는 지점(평형점)이 바로 라그랑주점이 됩니다. 

위 이미지는 https://astro.kasi.re.kr/learning/pageView/5233에서 따왔습니다

우선 결론 부터 설명하면, 태양-지구 시스템이 만들어내는 라그랑주점은 총 5개가 있습니다. 이 다섯개의 라그랑주 점을 각각 $L_1,L_2,L_3,L_4,L_5$라고 부릅니다. $L_1,L_2,L_3$는 태양-지구가 이루는 직선상에 있으며, $L_4,L_4$은 태양-지구-$L_4$는 정삼각형을 이루게 됩니다. $L_5$는 다른쪽 정삼각형의 꼭지점이 됩니다. 

 

태양과 지구가 그 자리에 고정 돼 있는 상황을 생각하면 (실제로는 태양-지구 중력으로 인해서 그럴 수 없습니다), 위성이 받는 힘은 위에서 설명한 $(1)+(2)$가 됩니다. 이 경우에는 태양과 지구 사이에 특정한 한 점(이 점에서는 (1)과 (2)의 힘의 크기가 같고 방향이 반대가 됩니다)을 제외하면 평형점은 있을 수 없습니다. 하지만, 실제로는 지구는 태양 주변을 공전하게 됩니다. 위성 역시 태양 주변을 공전하게 되는데, 따라서 이미 앞에서 설명한 것과 같이 $(1)+(2)$힘 뿐 아니라 공전에 의한 원심력인 힘 $(3)$을 받기 때문에, 힘 (1), (2), (3)이 적당히 밸런스를 이루는 지점에서 알짜힘 0이 됩니다. 이 점들이 바로 $L_1,L_2,L_3,L_4,L_5$ 입니다. 

 

그러면 이제 어떻게 하여 위 라그랑주 점 $L_1,L_2,L_3,L_4,L_5$를 얻을 수 있는지 계산해 보도록 하겠습니다. 

 

비관성 좌표계

 

뉴턴의 운동 법칙 $\overrightarrow{F}=m\overrightarrow{a}$를 적용하기 위해서는, 우선 입자의 위치, 속도, 가속도를 기술할 좌표계를 설정해야하는데, 이 좌표계는 관성계이어야 합니다. 관성계는 뉴턴의 운동 법칙 중 제 1법칙에 따라서 "입자에 아무런 힘이 가해지지 않는다면, 입자는 등속직선운동(정지 포함)을 하게 되는 좌표계" 입니다. 태양-지구-위성으로 이루어진 계에서는 태양의 중심을 원점으로 삼고, 우주 공간상에 정해진 고정된 세 축을 정해서 3차원 좌표계를 설정할 수 있습니다. (물론 태양 역시 우리 은하의 중심을 공전하고 있지만, 이는 무시하도록 하겠습니다) 이 좌표계를 이용하여 태양-지구-위성의 움직임을 기술하면, 태양은 원점에 정지 돼 있고, 지구와 위성은 태양 주변을 공전하게 됩니다. 

 

우리에게 관심있는 물리량은 위성이 받는 힘입니다. 따라서 위성만 움직이고, 태양과 지구가 고정 돼 있으면 좋겠는데, 앞에서 설명한 것 처럼 지구는 고정 돼 있지 않고 태양 주변은 공전하게 됩니다. 지구가 계속 움직이는 것을 생각하면 귀찮기 때문에, 태양 뿐 아니라 태양-지구가 모두 고정 돼 있는 좌표계를 생각하면 더 좋습니다. 위성의 질량이 태양과 지구의 질량에 비해서 매우 작다고 한다면(실제로 그렇습니다), 지구는 위성의 중력을 느끼지 못하고 단순히 태양으로 부터 받는 중력에 의한 원운동을 하게 됩니다. (일반적으로틑 타원 운동을 하게 되지만 편의상 원운동으로 생각하겠습니다. 실제로 원에 매우 가까운 타원입니다) 지구가 태양 주변을 각속도 $\mathrm{\Omega }$로 회전하고 있기 때문에, 만일 우리가 태양을 중심으로 각속도 $\mathrm{\Omega }$로 회전하는 회전 좌표계를 도입한다면, 이 좌표계에서는 태양과 지구가 모두 움직이지 않고, 고정 된 위치에 유지됩니다. 이것은 마치 회전 목마를 타고 있다면, 내 바로 앞에 있는 말이 항상 일정한 거리를 유지 한 채 내 앞에 있게 되는 것과 동일한 이치 입니다. 회전 목마 밖에 있는 사람이 본다면 두 말이 원운동을 하게 되지만, 회전 목마 안에서는 두 말은 고정 된 위치에 있게 되는 것 입니다. 여기서 회전 목마 밖을 관성계, 회전 목마 안을 회전하는 좌표계(비 관성계)로 볼 수 있습니다. 

 

이 처럼 각속도 $\mathrm{\Omega }$로 회전하는 좌표계를 도입하면 태양과 지구의 위치가 고정됩니다. 매우 편리합니다. 그러나, 이 좌표계는 관성 좌표계가 아니라 비관성 좌표계이기 때문에 뉴턴의 법칙이 성립하지 않습니다. 뉴턴의 법칙이 성립하기 위해서는 비관성 좌표계에 의해서 유도되는 "관성력"을 도입하여야 합니다. 

 

관성력 : 코리올리 힘과 원심력

 

각속도 $\mathrm{\Omega }$로 회전하는 좌표계에서도 뉴턴의 운동 법칙을 적용하기 위해서는 "관성력"을 도입해야 합니다. 유도는 생략한 채, 결과만 본다면 실제로 입자(위성)에 가해지는 힘을 $\overrightarrow{F}$라고 할 때, 

$${\overrightarrow{F}}_{\mathrm{\Omega }}=\overrightarrow{F}-2m\overrightarrow{\mathrm{\Omega }}\times \overrightarrow{v}-m\overrightarrow{\mathrm{\Omega }}\times (\overrightarrow{\mathrm{\Omega }}\times \overrightarrow{r})$$

이 힘을 ${\overrightarrow{F}}_{\mathrm{\Omega }}$로 "바꿔주면" 비관성계에서 뉴턴의 운동 법칙을 그대로 사용할 수 있습니다. 위 식의 두 번째, 세번째 항의 힘이 관성력인데, 두 번째 힘을 코리올리 힘, 세 번째 힘을 원심력이라고 합니다. 

 

힘 뿐만 아니라 위치 에너지 역시 식이 바뀌게 되는데, 

$$U_{\mathrm{\Omega }}=U-\overrightarrow{v}\cdot (\overrightarrow{\mathrm{\Omega }}\times \overrightarrow{r})-\frac{1}{2}(\overrightarrow{\mathrm{\Omega }}\times \overrightarrow{r})\cdot (\overrightarrow{\mathrm{\Omega }}\times \overrightarrow{r})$$

이 되고, "일반화된 미분"에 의해서

$${\overrightarrow{F}}_{\mathrm{\Omega }}=-{\mathrm{\nabla }}_{\overrightarrow{r}}{U}_{\mathrm{\Omega }}+\frac{d}{dt}{\mathrm{\nabla }}_{\overrightarrow{v}}{U}_{\mathrm{\Omega }}$$

가 됩니다. 위 식의 유도 과정과 의미는 고전 역학 교과서의 비관성 좌표계를 다루는 부분을 보면 됩니다. 

위 결과에 따라서 위성에 가해지는 위치 에너지는, $\overrightarrow{\mathrm{\Omega }}=\mathrm{\Omega }\hat{z}$라고 하고, 우선은 간단하게 위성의 속도를 0으로 둔다면,

$$U_{\mathrm{\Omega }}=U-\frac{1}{2}{\mathrm{\Omega }}^2{r}^2$$

이 됩니다. 여기서 $U$는 태양-위성, 지구-위성의 중력에 의한 위치에너지로 이를 풀어서 쓰면,

$$U_{\mathrm{\Omega }}=-\frac{G{M}_1}{|\overrightarrow{r}-{\overrightarrow{r}}_1|}-\frac{G{M}_2}{|\overrightarrow{r}-{\overrightarrow{r}}_2|}-\frac{1}{2}{\mathrm{\Omega }}^2{r}^2$$

가 됩니다. 여기서 ${\overrightarrow{r}}_1,{\overrightarrow{r}}_2$ 는 각각 태양, 지구의 위치이며 $M_1,M_2$는 각각 태양, 지구의 질량입니다. $G$는 중력상수입니다. 위 식에서는 위 그림과 같은 좌표계를 사용했습니다. 

 

위성이 받는 위치 에너지와 라그랑주 점

 

위 식에 따라서 위성이 받는 위치 에너지를 한 번 그려 보도록 하겠습니다. 당연히 이 위치 에너지는 실제 위치 에너지가 아닌 "태양-지구가 고정된 비관성계"에서 적용되는 "일반화된 위치 에너지" 입니다. 결과를 간단히 하기 위해서 $R=|{\overrightarrow{r}}_1-{\overrightarrow{r}}_2|=10,M_1=10,M_2=1$ 를 사용해 보도록 하겠습니다. 역시 $v=0$ 입니다. 

위치 에너지를 등고선으로 그리면 위와 같습니다. 파란색이 값이 작는 부분, 붉은색이 값이 큰 부분입니다. 검은색 점이 원점이자 질량 중심, 붉은색 점이 $M_1$의 위치 푸른색점이 $M_2$의 위치 입니다. $\frac{M_1}{M_2}=10$이기 때문에 질량 중심은 $M_1$의 위치에 가깝습니다. $L_1,L_2,L_3,L_4,L_5$ 로 표시한 점이 다섯 개의 라그랑주 점으로, 각 점에서는 위치 에너지가 극값이 되기 때문에 힘이 0이 됩니다. 

위 그래프는 $y=0$ 에서 $x$값에 따른 위치 에너지를 그린것 입니다. 위치 에너지의 미분이 0이 되는 점을 세 곳 찾을 수 있는데, 이 점들이 왼쪽 부터 $L_3,L_1,L2$ 입니다. 

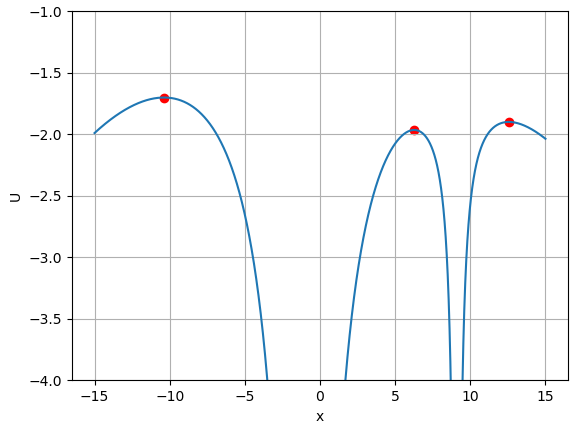
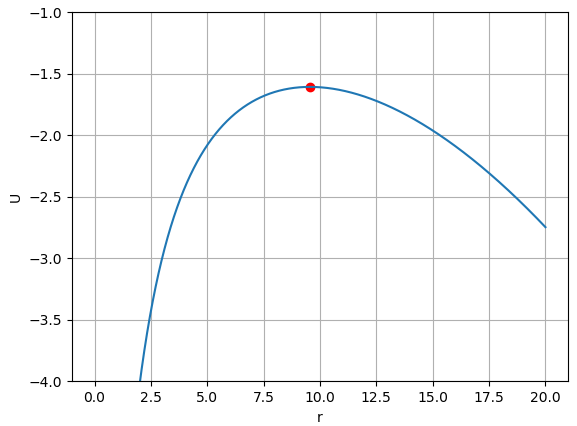
위 그래프는 원점에서 $\theta =\frac{\pi }{3}$ 방향으로 선을 그었을 때, 원점에서 부터 거리에 따른 위치 에너지를 그린 것 입니다. 위치 에너지 등고선 그림에서 원점에서 부터 $L_4$방향으로의 반직선을 생각하면 됩니다. 위치 에너지의 미분이 0이 되는 곳을 한 점 찾을 수 있는데, 그곳이 바로 $L_4$ 입니다. 

 

라그랑주 점에서의 안정성

 

평형점(equilibrium)을 찾으면 그 다음으로 해야 하는 것은 해당 평형점이 안정적인 평형점인지 아니면 불안정적인 평형점인지를 확인하는 것 입니다. 

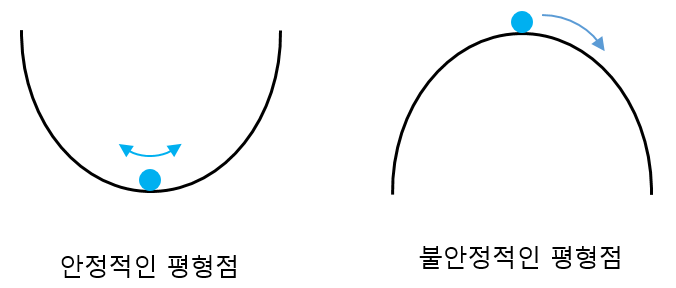
안정적인 평형점은 위 그림의 왼쪽과 같이, 평형점에서 약한 외력에 의해서 위치가 약간 어긋났을 때, 입자가 평형점에 다시 돌아 오면서 평형점 주변을 진동하게 되는 평형점이고, 불안정적인 평형점은 평형점에서 약한 외력에도 입자가 평형점을 크게 벗어나는 평형점을 말합니다. 안정적인 평형점 근처에서 위치 에너지는 아래로 볼록한 형태를 갖고, 불안정적인 평형점 근처에서는 위로 볼록한 형태를 갖습니다.

 

평형점으로 부터 약간의 위치 변화 $\delta x=x-x_{eq}$에 따른 속도 $\frac{d}{dt}\delta x$가 어떻게 되는지를 통해서도 평형점이 안정적인 혹은 불안정적인 평형점을 확인할 수 있습니다. 평형점 근처에서 선형 근사를 취했을 때, 위치와 속도의 관계가

$$\frac{d}{dx}(\delta x)=\lambda (\delta x)$$

와 같이 표현 된다면, 근사적으로 $\delta x(t)=e^{\lambda t}\delta x(0)$ 이 됩니다. 이 때, $\lambda >0$이라면 $\delta x$는 발산하게 됩니다. 즉, 위 그림에서 불안정적인 평형점 그림에서 처럼 평형점에서 점점 멀어집니다. $\lambda$가 허수인 경우, $e^{i\theta }=\cos \theta +i\sin \theta$에 따라서 $\delta x$는 원점을 기준으로 진동하게 되고, 이는 안정적인 평형점이 됩니다. 

 

위 방법을 통해서 다섯 개의 라그랑주 점의 안정성을 체크 해 보겠습니다. 각 라그랑주 점(평형점)에서 위치와 속도를 아주 약간식 변화 시켰을 때, 즉

$$x=x_{L_i}+\delta x$$

$$y=y_{L_i}+\delta y$$

$$v_x=\delta v_x,$$

$$v_y=\delta v_y$$

에 대해서, 위치와 속도의 변화를 선형 근사를 통해 표현할 수 있습니다. $\overrightarrow{v}\ne 0$ 인 상황을 고려하고 있기에, 코리올리 힘이 포함된 위치 에너지 혹은 힘의 식을 이용해야 합니다. 약간의 계산을 거치면,

$$\frac{d}{dt}\left(\begin{array}{c}\delta x\\ \delta x\\ \delta v_x\\ \delta v_y\end{array}\right)=\left(\begin{array}{cccc}0& 0& 0& 1\\ 0& 0& 0& 1\\ \frac{d^2{U}_{\mathrm{\Omega }}}{d{x}^2}& \frac{d^2{U}_{\mathrm{\Omega }}}{dxdy}& 0& 2\mathrm{\Omega }\\ \frac{d^2{U}_{\mathrm{\Omega }}}{dxdy}& \frac{d^2{U}_{\mathrm{\Omega }}}{d{y}^2}& -2\mathrm{\Omega }& 0\end{array}\right)\left(\begin{array}{c}\delta x\\ \delta y\\ \delta v_x\\ \delta v_y\end{array}\right)$$

를 얻습니다. 여기서 $U_{\mathrm{\Omega }}$의 미분은 라그랑주 점에서의 미분을 뜻 합니다. 

 

위 벡터 미분 방정식은 벡터에 4개의 성분을 갖지만, 기본적인 형태는

$$\frac{d}{dt}\mathit{\delta }=\mathbf{\Lambda }\mathit{\delta }$$

와 같은 형태로 쓰여질 수 있고, 하나의 $\lambda$ 값 대신에 $\mathrm{\Lambda }$ 행렬의 고유값을 사용해야 합니다. 

 

다섯 개의 라그랑주 점에서의 $\mathrm{\Lambda }$ 행렬의 값을 실제로 계산하고, 행렬을 대각화 하면 됩니다. 이는 조금 귀찮은 계산인데, 결과만 쓰자면,

 

$L1,L2$ 점에서는 

$$\pm \mathrm{\Omega }\sqrt{11+2\sqrt{7}},\pm i\mathrm{\Omega }\sqrt{2\sqrt{7}-1}$$

의 고유값을 갖습니다. 양수 고유값이 있기에, 불안정적인 평형점이 됩니다. 

 

$L_3$ 점에서는

$$\pm \mathrm{\Omega }\sqrt{\frac{3M_1}{8M_2}},\pm i\mathrm{\Omega }\sqrt{7}$$

의 고유값을 갖습니다. 이 점에서 역시 양수 고유값이 있기에, 불안정적인 평형점이 됩니다. 

 

$L_1,L_2,L_3$ 점은 평형점이긴 하지만, 이 점에서 약간만 벗어나거나, 약간의 속도가 있기만 한다면 평형점에서 부터 멀리 벗어나게 됩니다. 

 

$L_4,L_5$ 점에서는 $\kappa =\frac{M_1-M_2}{M_1+M2}$ 라고 할 때,

$$\pm i\frac{\mathrm{\Omega }}{2}\sqrt{2\pm \sqrt{27{\kappa }^2-23}},$$

의 고유값을 갖습니다. 제곱근 안의 값이 양수가 된다면, 네 개의 고유값이 모두 허수를 갖기 때문에, $L_4,L_5$는 안정적인 평형점이 됩니다. 위 조건은

$$M_1\ge 25M_2(\frac{1+\sqrt{1-\frac{4}{625}}}{2})$$

입니다. 즉, 질량이 큰 행성의 질량($M_1$)이 질량이 작은 행성의 질량($M_2$) 보다 약 25배 이상 크다면, $L_4,L_5$ 라그랑주 점은 안정적인 평형점이 됩니다. 실제로 태양-지구계 에서는 태양의 질량이 지구의 질량에 비해 훨씬 크기 때문에, $L_4,L_5$는 안정적인 평형점이 됩니다. 

 

https://astronomy.stackexchange.com/questions/373/parking-a-telescope-at-a-lagrange-point-is-this-a-good-idea-from-a-debris-point에서 따왔습니다.

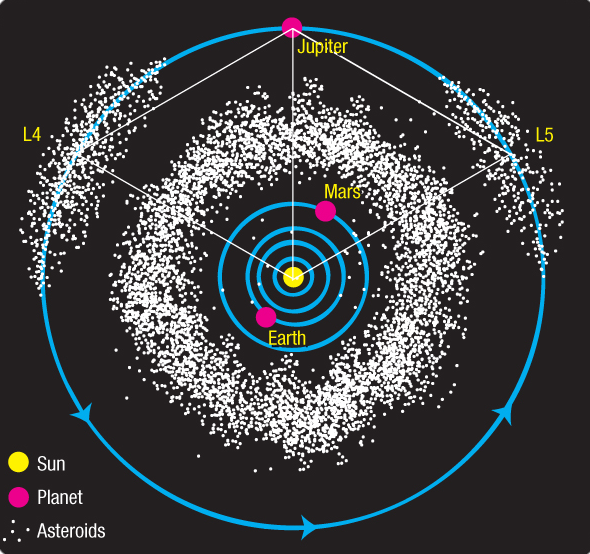
태양계는 사실상 태양-목성으로 이루어진 시스템으로 볼 수 있습니다. 따라서, 태양계에 속박된 소행성들은 위에서 태양-지구-위성 시스템의 위성과 같이 태양-목성으로 부터 중력과 회전에 의한 원심력을 받습니다. 소행성이 안정적인 평형 상태인 라그랑주 점 $L_4,L_5$ 부근에서 (다양한 이유로) 속도가 작아 진다면 $L_4,L_5$ 라그랑주 점에 속박된 상태를 계속 유지 할 수 있습니다. 그 결과 위 그림과 같이 태양계의 많은 소행성들이 태양과 목성으로 인해 형성되는 라그랑주 점 $L_4,L_5$에 속박 돼 있게 됩니다. (화성과 목성 사이에도 수 매우 많은 소행성들이 위치 합니다. 정확한 이유는 모르겠으나, 이 영역 역시 라그랑주 점과는 다른 이유로 안정적인 평형점을 유지할 수 있을 것 입니다)

 

위 포스팅의 내용은 https://map.gsfc.nasa.gov/ContentMedia/lagrange.pdf 를 참고하였습니다. 좀 더 상세한 유도 과정을 알고 싶으신 분은 해당 자료를 참고하면 됩니다.