고전역학에서는 꼭 배워야 하는 혹은 풀이법을 알아야 하는 문제(주제)들이 있는데, 그 중에서 하나는 이번 포스팅에서 알아 볼 원형 빗면에서 구르는 입자의 운동에 대한 문제 입니다.
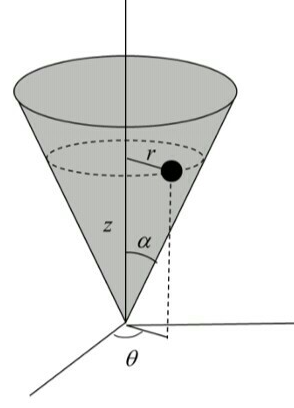
위 그림과 같이 속이 비었고, 원형 바닥이 빈 원뿔을 뒤집어 놓는 구조에서 구슬을 빗면을 따라 굴리는 현상을 기술하는 문제 입니다. 일상생활에서도 이런 현상을 가끔씩 접할 수 있는데, 위 그림과 같은 원뿔이 아니라도 바구니나 그릇안에 담겨 있는 구슬을 손가락으로 강하게 쳐서 구슬이 속도를 갖게 하면, 구슬은 그릇 안을 빙글 빙글 돌게 됩니다. 구슬의 초기 속도가 매우 크다면, 구슬은 그릇면의 높은 곳 까지 올라가서 빠르게 원운동을 할 것이며, 약하게 굴리면 구슬은 타원형 비슷한 궤도를 그리며 구슬의 제일 낮은 점 근처를 배회할 것 입니다.
이번 포스팅에서는 위 그림과 같이 콘 벽면에 놓인 입자의 움직임을 기술해 보도록 하겠습니다. 당연히 문제를 편히 하기 위해서 입자는 질점으로 취급할 것이며, 이 경우 실제 구슬의 회전 운동을 무시하는 것이 됩니다, 이 질점과 콘 벽면 사이의 마찰 및 공기 저항은 모두 무시할 것 입니다. 그리고 당연히 지표면에 수직하는 균일한 중력장이 있다고 가정하겠습니다.
일반화 좌표
위 문제는 당연히 라그랑지안 역학의 방법론으로 풀어야 합니다. 질점의 운동은 3차원 운동이지만, 콘의 벽면에 제한된 운동이기 때문에 실제로는 2차원 운동이라 할 수 있으며, 따라서 질점의 위치를 기술하는 일반화 좌표를 2차원 입니다. 위 그림을 보면 2개의 일반화 좌표는 당연히 $(r, \theta)$임을 알 수 있습니다.
질점의 속도와 운동에너지
임의의 점에서 질점의 움직임은 (1)반지름 $r$이 동일한 방향으로의 움직임과 (2)각도 $\theta$가 동일한 방향으로의 움직임으로 나눌 수 있습니다. (1)은 일정한 높이에서 콘을 빙글 빙글 도는 움직임이고, (2)는 특정한 방향에서 콘의 벽면을 따라서 위 혹은 아래로 움직이는 것 입니다. (1)방향의 움직임은 (반지름이 바뀌지 않은) 원운동이고 원운동의 속력에 대한 식으로 부터 $v_{\theta} = r \dot{\theta}$가 됩니다. 여기서 $\dot{\theta} = \frac{d \theta}{dt}$로 각속도입니다. (2)방향의 움직임은 단순 직선 움직임으로 빗면 방향의 이동 거리를 시간으로 미분하면 됩니다. 빗면 방향으로의 변위는 $r$의 변위를 $\sin \alpha$로 나눈 것과 동일 하므로, 즉 $l \sin \alpha = r$ 여기서 $l$은 빗면 방향의 변위, 빗면 방향의 속도는 $v_r= \frac{1}{\sin \alpha} \dot{r}$ 이 됩니다.
위 식으로 부터 질점의 운동에너지는
$$T = \frac{1}{2}mv^2 = \frac{1}{2}m(v_\theta^2 + v_r^2) = \frac{1}{2}m \Big(r^2 \dot{\theta}^2 + \frac{1}{\sin^2 \alpha}\dot{r}^2 \Big) $$
이 됩니다. 일반적인 2차원 평면 운동에서 운동에너지를 극좌표로 표현했을 때와 비교하면 $\frac{1}{\sin \alpha}$가 추가로 도입된 것 이외에는 차이가 없습니다. $\alpha = \frac{\pi}{2}$ 인 경우, 즉 원뿔의 벽면이 지표면에 닿는 경우, 2차원 평면 운동에서의 식과 동일하게 됩니다.
질점의 위치에너지
질점의 위치에너지는 질점의 높이를 알면 되는데, 높이이 기준(즉 위치 에너지의 기준)을 원뿔의 꼭지점의 위치로 하도록 하겠습니다. 이 경우 위 그림에서 질점의 높이 $h$는 $h = \frac{1}{\tan \alpha} r$ 이 됩니다. 따라서 위치에너지는 $mg \frac{1}{\tan \alpha} r$ 이 됩니다.
질점의 운동을 기술하는 라그랑지안
위치에너지와 운동에너지를 다 구했으니, 라그랑지안은
$$L = T - V = \frac{1}{2}m \Big(r^2 \dot{\theta}^2 + \frac{1}{\sin^2 \alpha}\dot{r}^2 \Big) - mg \frac{1}{\tan \alpha} r$$
입니다. 오일러-라그랑지 방정식을 통해서 위 문제를 풀면 됩니다. $r, \theta$에 대한 각각의 오일러-라그랑지 방정식을 계산하면 $r, \theta$에 대한 연립 미분 방정식을 얻게 되고, 그 미분 방정식을 풀면 됩니다. 물론 해석적인 방법으로 푸는 것은 어려우니 필요한 경우엔 수치해석적인 방법으로 풀면 됩니다.
라고 포스팅을 마치면, 이건 물리학과 관련된 주제라기 보다는 기계공학의 내용을 다루는 포스팅이 될 것 입니다. 하지만 이 글은 "물리학" 카테고리의 글이니, 보다 "물리학적인 방법"을 통해서 위 라그랑지안을 다루어 보도록 하겠습니다.
보존량
보존량은 물리학에 등장하는 수 많은 개념 중에서 둘째 가라면 서러울 정도로 중요한 개념입니다. 그 만큼 개념적으로도 중요하고, 또한 문제를 푸는데도 매우 중요한 개념 입니다. 특정한 물리량이 보존되는 것을 안다면, 그 물리량과 관련된 다른 물리량들의 관계를 쉽게 유도할 수 있기 때문입니다. 따라서 문제의 라그랑지안이 주어졌을 때, 처음으로 해야할 일은 바로 보존량을 찾는 것 입니다.
위 문제의 일반화 좌표는 $r, \theta$ 이므로 라그랑지안은 $r, \theta, \dot{r}, \dot{\theta}$의 함수가 됩니다. 그런데 이 문제의 라그랑지안에는 $\theta$가 보이지 않습니다. 따라서 $\theta$의 켤레운동량(conjugate momentum)이 보존량이 됩니다. 오일러-라그랑지 방정식을 통해서 설명하자면, $\theta$에 대한 오일러-라그랑지 방정식은
$$\frac{\partial L}{\partial \theta} = \frac{d}{dt} \Big( \frac{\partial L}{ \partial \dot{\theta}} \Big)$$
인데,
$L$의 식에 $\theta$가 등장하지 않기 때문에, $\frac{\partial L}{\partial \theta} = 0$이 되고, 따라서 $\frac{\partial L}{ \partial \dot{\theta}}$ 값은 시간에 대해 무관한 값이 됩니다. 이 값이 만일 시간에 따라 변하는 값이라면, 위 식의 우항이 0이 아닌 값이 되므로 모순이 됩니다. $\frac{\partial L}{ \partial \dot{\theta}}$는 $\theta$에 대한 켤레운동량의 정의이며, 이 값을 $M$로 정의 하도록 하겠습니다. (M 대신 L 을 사용하고 싶지만, 이 경우 라그랑지안의 L과 혼동이 될 수도 있습니다) 정리하면,
$$M = \frac{\partial L}{ \partial \dot{\theta}} = mr^2 \dot{\theta} \text{ (constant)}$$
이 값은 다름 아닌 각운동량입니다. 위 식은 $r$과 $\dot{\theta}$가 마음대로 변할 수 있는 것이 아니라 항상 특정한 조건을 만족하면서 변해야 함을 알려주고 있습니다. 이를 통해서 두 변수 중 한 변수를 소거 할 수 있는데, $\theta$를 소거하는 편이 더 편리합니다. 즉,
$$\dot{\theta} = \frac{M}{mr^2}$$
로 $\dot{\theta}$를 $r$에 대한 식으로 쓸 수 있습니다. 각 운동량 M은 문제의 초기 조건에 의해 정해지게 됩니다.
$r$에 대한 운동 방정식 : 정성적으로 알아 보기
이 문제의 일반화 좌표는 2개였는데, 보존량을 이용하여 $r$에 대한 "1차원 문제"로 문제의 차원을 줄였습니다. $r(t)$를 구하고 난 뒤, $\dot{\theta} = \frac{M}{mr(t)^2}$ 관계식을 이용하여 $\theta(t)$를 바로 구할 수 있습니다. $r$에 대한 방정식을 풀면 되는데, $r(t)$를 구하는 것도 좋지만, 그 전에 정성적으로 $r(t)$가 어떠한 범위 내에서 움직일 수 있는지에 대해서 알아 보겠습니다. 즉, $r_{min} \le r(t) \le r_{max}$ 가 되는 $r_{min}, r_{max}$를 먼저 찾아 보겠습니다.
시스템의 역학적 에너지를 $r, \dot{r}$에 대한 식으로 쓰면,
$$E = \frac{1}{2}m \frac{1}{\sin^2 \alpha}\dot{r}^2 + \frac{1}{2} \frac{M^2}{mr^2} + mg \frac{1}{\tan \alpha} r$$
가 됩니다. $\theta$의 의존성은 원래 부터 없었고, $\dot{\theta}$의 의존성은 $\dot{\theta} = \frac{M}{mr^2}$으로 치환하였습니다. 위 $E$를 $\dot{r}$에 대한 항과 $r$에 대한 항으로 나눠서 쓰면,
$$E = \frac{1}{2}m \frac{1}{\sin^2 \alpha}\dot{r}^2 + V_{eff}(r)$$
$$V_{eff}(r) =\frac{1}{2} \frac{M^2}{mr^2} + mg \frac{1}{\tan \alpha} r$$
와 같이 $V_{eff}(r)$을 도입하여 쓸 수 있습니다. $E$의 첫 번째 항은 $r$의 운동에너지 항이고, 그 외의 항은 효율적인(effective) 위치에너지로 놓을 수 있습니다. $V_{eff}(r)$의 두 번째 항은 단순한 중력에 의한 위치 에너지 이고, 첫 번째 항은 각운동량에 의한 위치 에너지 인데, 이를 "원심력에 의한 위치 에너지"라고 생각할 수 있습니다. 물론 아시겠지만, 원심력은 실제 힘이 아니라서 "원심력에 의한 위치 에너지" 같은 물리량은 정의가 되지 않지만, 단순히 수식을 해석할 때는 "원심력"에 의한 항이라고 생각해도 크게 틀리지 않습니다.
$V_{eff}(r)$을 그래프로 그려보면,
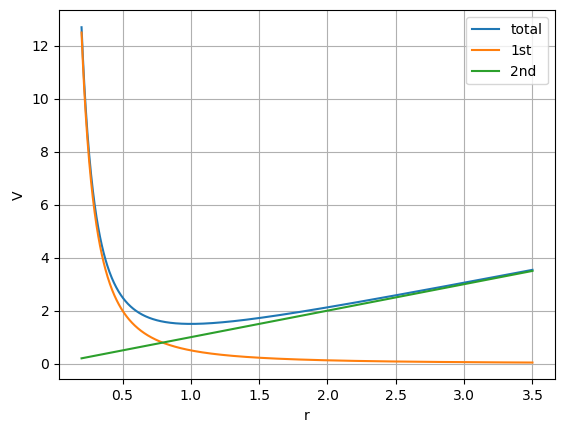
위와 같습니다. 편의상 $m=1, M = 1, g = 1, \tan \alpha = 1$ 인 경우를 생각하였습니다. 위 $r-E$ 그래프로 부터 $r$에 대한 운동을 정성적으로 설명할 수 있습니다. 이 개념을 이해하는 것이 상당히 중요합니다. 보통 1차원 운동에서 $x-E$ 그래프를 그리고 이를 통해서 질점의 운동 범위 ($x$의 범위), 각 지점에서의 속도 등을 이해하는 것과 동일합니다. 단지 $x$가 $r$로 바뀐 것 뿐 입니다.
주황색으로 그린 "원심력에 의한 위치 에너지"는 $r$이 커질 수록 그 값이 작아지는데, 이는 원심력은 원운동에서 원의 중심에서 더 밖으로 나가게 하는 (r이 커지게 하는) 힘이기 때문입니다. 반대로 녹색으로 그린 중력에 의한 위치 에너지는 $r$이 작아지는 방향을 "선호"하는데, 이는 당연히 질점의 높이가 낮아지면 반지름이 작아지기 때문입니다.
질점의 역학적 에너지가 $E_0$로 주어진 경우, $r_{min}, r_{max}$ 값은 $V_{eff}(r) = E_0$를 만족하는 $r$값이 됩니다. $r_{min}, r_{max}$에서는 $\dot{r} = 0$이 되고, $r$방향의 운동의 방향이 바뀌게 됩니다. 그 중에서 더 작은 값이 $r_{min}$ 큰 값이 $r_{max}$가 됩니다. 예를들어, $E_0 = 3.0$ 이라면 (단위는 그래프 아래에 설명한 단위를 사용했을 때의 에너지 단위 입니다),

$r_{min} = 0.4, r_{max} = 2.9$가 됩니다. 즉, 입자의 $r(t)$는 $0.4 \le r(t) \le 2.9$ 범위에서 진동 운동을 하며, 그러는 동안에 $\theta(t) = \int^{t} \frac{M}{mr(t)^2}dt + \theta_0$의 운동을 하게 됩니다. $r$이 작을수록 $\dot{\theta}$가 커지기 때문에, 원점(원뿔의 뾰족한 꼭지점)에 가까우면 가까울 수록 회전하는 양상이 빨라집니다. $r(t)$를 해석적으로 구하기가 매우 어렵기 때문에, 개념적으로만 이해할 수 있습니다.
$V_{eff}(r)$는 순수하게 $M$의 함수 입니다. 즉, 초기 조건에 의해서 $M$이 결정이 되면 $V_{eff}(r)$의 형태가 완전히 결정이 되고, 역시나 초기 상태에 의해서 결정되는 $E_0$ 값에 따라서 질점의 운동의 최소/최대 반지름 $r_{min}, r_{max}$가 결정됩니다. $M$이 정해진 상태에서 질점의 운동 에너지가 가장 작을 때는 $\dot{r} = 0$인 상태로, 이 때는 원운동을 하게 됩니다. 위 그래프를 통해서 설명하면 질점의 역학적 에너지가 $V_{eff}(r)$의 최소값과 같다면, 그 값은 약 $E_0 = 1.5$ 이고, 이때는 $r_{min} = r_{max} = 1.0$이 됩니다. $r_{min} = r_{max}$이라는 것은 반지름이 항상 같다는 뜻으로 원운동을 의미합니다. $M$이 정해진 상태에서 역학적 에너지기 최소일때의 운동은 원운동이라는 것을 알고 있는 것은 중요합니다.
$r$에 대한 운동 방정식 : 수치해법으로 풀어 보기
$V_{eff}(r)$로 부터, $r$에 대한 시간에 따른 미분 방정식은 $\frac{d^2r}{dt^2} = -\frac{dV_{eff}(r)}{dr}$ 을 얻을 수 있고, 이 미분 방정식을 룽게-쿠타 방법론과 같은 수치해법으로 풀 수 있습니다. $r(t)$을 얻은 이후에, $\theta(t) = \int^{t} \frac{M}{mr(t)^2}dt + \theta_0$를 통해서 $\theta(t)$역시 구할 수 있습니다. $(r(t), \theta(t))$를 이용하여 원래 3차원 공간에서의 좌표 $(x(t), y(t), z(t))$ 역시 구할 수 있습니다.

위 에니메이션은 운동 방정식을 수치해법으로 푼 결과 입니다. $\alpha = \frac{\pi}{4}$ 인 콘의 형태를 사용하였고, 물리 상수는 $m = 1kg, g = 9.8m/s^2$를 사용하였습니다. (이후 부터 길이의 단위는 $m$, 속도의 단위는 $1/s$ 입니다. 편의상 생략하였습니다) 질점 운동의 초기 조건은 $r = 2.0, \theta = 0, \dot{r} = 0, \dot{\theta} = 100 \frac{\pi}{180}$ 입니다. 위 시뮬레이션의 초기 높이는 $z = 2m$ 인데, 초기 각속도 $\dot{\theta} = 100 \frac{\pi}{180}$는 원운동을 하기에는 부족한 각속도 이기 때문에, 초기 높이($\alpha = \frac{\pi}{4}$인 경우에는 높이나 $r$이나 그 값이 같습니다)가 감소하게 됩니다. 대략 $z = r = 1.5$만큼 감소하다가 다시 즘강해서 약 $z = r = 2$까지 되돌아 오게 됩니다. $X-Z$ 평면으로 사영(projection)시킨 녹색 궤적을 보면 이를 쉽게 알 수 있습니다. 높이가 낮아지면 중력가속도에 의해서 속도가 증가하게 되고, 속도가 증가하게 되면 "원심력"에 의해서 밖으로 튀어 나가려고 하기 때문에 반지름이 커지고, 따라서 높이도 높아지는 것 입니다. $X-Y$ 평면으로 사용시킨 오렌지색 궤적을 보면 질점의 운동이 원운동에서 조금 벗어나 있음을 볼 수 있습니다.

동일한 조건에서 초기 각속도를 $\dot{\theta} = 130\frac{\pi}{180}$ 으로 증가시켰습니다. 이 경우에는 거의 원운동을 하게 되며, 높이 역시 초기 높이 $z = r = 2$를 유지하게 됩니다. 실제 현상에서는 공기 저항과 질점과 벽면과의 마찰로 인해서 운동에너지가 열에너지 등으로 전환이 되고, 따라서 속도가 점점 줄어들면서 원뿔의 바닥으로 추락하게 될 것 입니다. 그러나 이 시뮬레이션에서는 역학적 에너지 손실을 고려하지 않았기 때문에, 위와 같이 거의 일정한 높이에서 (거의) 등속원운동을 하게 됩니다.

초기 각속도를 $\dot{\theta} = 170\frac{\pi}{180}$ 으로 증가시켰습니다. 초기 속도가 매우 크고 따라서 "원심력"이 매우 크게 작용하여 입자가 거의 콘 밖으로까지 나가려고 합니다.

이번에는 초기 각속도를 $\dot{\theta} = 50\frac{\pi}{180}$ 으로 감소시켰습니다. 이 경우에는 초기 높이 $z = r = 2$를 유지할 만큼 속도가 큰 것이 아니기 때문에 높이는 $z = r = 0.5$ 정도까지 금격하게 감소하게 됩니다. 그렇다고 해서 $z = 0$ 까지 갈 수 있는 것은 아니고, 감소한 위치 에너지 만큼 운동 에너지가 커지기 때문에 다시 "원심력"을 받아서 원래 높이까지 올라가게 됩니다. 초기 각속도가 0이 아니라면, 초기 각운동량 역시 0이 아닌 값이 되고, 각 운동량이 0이 아니라면 운동량 보존법칙에 따라서, 질점은 바닥 $z = r = 0$에는 도달할 수 없습니다.
정리 : 핵심은 각운동량 보존
위 결과를 정리 해 보겠습니다. 사실 정리를 할 만큼 내용이 그리 많지는 않지만, 중요한 사항은 반복하여 설명하는 것이 맞겠죠! 위 문제 풀이의 핵심은 각운동량 보존입니다. 각운동량 보존을 이용하여 2차원 문제(일반화 좌표가 2개인 문제)를 1차원 문제(하나의 일반화 좌표에 대한 문제)로 바꾸어 놓았습니다. $(r, \theta)$의 문제를 단순히 $r$만의 문제로 바꾼 것 입니다. 그렇게 얻은 $r$에 대한 1차원 문제는 $V(r)$이 $V_{eff}(r)$와 같이 "원심력"에 의한 위치 에너지가 도입된 "효과적인" 위치에너지에 대한 질점의 문제를 푸는 것으로 바뀌었습니다. 1차원 문제는 룽게-쿠타 방법과 같이 잘 알려진 수치 미분 방정식을 통해 풀 수 있기 때문에, 위와 같이 시뮬레이션도 얻을 수 있었습니다. 이 처럼 고차원 문제의 경우, 시스템의 보존량을 구해낸다면 실질적인 문제의 차원을 보존량의 갯수 만큼 줄일 수 있습니다.
이번 포스팅과 같은 문제 풀이 방법은 각운동량이 보존되는 임의의 시스템에서 사용될 수 있습니다. 학부 역학 교과서에서는 이 방법은 케플러 문제를 푸는데 도입됩니다. 케플러 문제에서 입자의 위치 에너지는 $-\frac{1}{r}$와 같이 주어지는데, 이번 문제에서는 위치 에너지나 $mgr$와 같이 바뀐 것 이외에는 아무런 차이가 없습니다. 위치 에너지의 구체적인 크기의 차이는 있지만, 모두 원의 중심($r = 0$ 방향)을 향한다는 것에 공통점이 있기 때문에, 정성적으로는 "같은" 운동으로 볼 수 있습니다. 입자를 받쳐주는 물체가 원뿔이 아니라 특정한 형태의 곡면으로 잘 만들어서 위치에너지가 $-\frac{1}{r}$이 되도록 만든다면 이 곡면에서의 물제의 운동과 행성의 운동은 완전히 "같은" 형태를 취할 것 입니다.
'물리학' 카테고리의 다른 글
| 중심력장 하에서 입자의 운동 (1) : 수치 미분 방정식 해법을 이용하여 문제 풀기 + 파이썬 시뮬레이션 코드 (0) | 2022.04.09 |
|---|---|
| 공전하는 두 천체가 만들어내는 평형점 : 라그랑주 점(Lagrange point) (1) | 2022.04.04 |
| [양자역학 문제 풀이]1차원 디랙 델타 포텐셜이 나오는 문제 (서울대 대학원 입학시험) (0) | 2022.03.28 |
| 양자역학 무한 포텐셜 우물 문제(infinite potential well)를 행렬역학의 방법으로 풀기 (2) | 2022.03.25 |
| 행렬역학과 파동역학이 동치임을 밝힌 슈뢰딩거 (0) | 2022.03.20 |


