렌즈, 물방울에 의한 빛의 굴절 : 공간에 따라 굴절률이 변하는 상황에서 Eikonal 방정식 풀기 + 신기루 현상 설명

지난 포스팅에서 Eikonal 방정식에 대해서 알아 봤습니다. Eikonal 방정식은 공간에 따라 굴절률이 변할 때, 빛의 경로에 대한 방정식이었습니다. 페르마의 원리로 부터 오일러-라그랑쥬 방정식을 세울 수 있고, 오일러-라그랑쥬 방정식을 굴절률, 위치, 길이 매개화의 미분으로 표현한 식이 바로 Eikonal 방정식이었습니다. Eikonal 방정식은, 굴절률이 서로 다른 두 매질 사이에서 굴절에 대한 관계식인 스넬의 법칙의 일반화라고 할 수 있습니다. https://studyingrabbit.tistory.com/85

빛의 진행 경로와 페르마의 원리와 Eikonal(아이코널) 방정식 : 페르마의 원리로 부터 스넬의 법칙

또한, 지난 포스팅에서는 Eikonal 방정식을 수치해법으로 푸는 방식을 설명하고, 이를 통해 스넬의 법칙을 수치해법을 통해서 알아 보았습니다. 빛의 입사의 초기 조건을 다양하게 바꿔 가면서, 전반사 현상을 시뮬레이션으로 확인하기도 했습니다. 

 

이번 포스팅에서는 조금 더 다양한 조건, 즉 공간에 따른 물질의 굴절률 $n(x,y,z)$가 다양한 형태, 에 대해서 수치해법으로 Eikonal 방정식을 풀고, 이로 부터 빛의 경로가 어떻게 주어지는지 알아보겠습니다.

 

해석적인 방법으로 문제를 푸는 것을 선호하는 입장이라면, 이번 포스팅에서와 같이 구체적인 문제를 수치해법으로 푸는 것에 대해서 별다른 의미나 재미를 느끼지 못 할 수 도 있습니다. 하지만, 단순히 방정식의 해를 종이에 수식으로 쓰는 것과 구체적인 문제를 풀어서, 해의 형태를 시각적으로 표현하는 것은 완전히 다른 일이며, 이것은 해석적인 방법으로 문제를 푸는 것에도 매우 큰 도움을 줍니다. 뿐만아니라 구체적인 문제를 풀 때는 매우 구체적인 방식의 모델링과 방정식을 푸는 구체적인 테크닉이 필요한데, 이를 통해서도 많은 것을 배울 수 있습니다.

 

문제의 풀이, 시각화, 설명을 간단히 하기 위해서 2차원 문제로 제한해서 생각하겠습니다. 즉 공간은 $(x,y)$로 기술될 수 있으며 굴절률 역시 $n(x,y)$로 기술 될 수 있습니다. 일반적인 3차원으로의 확장은 독자분께서 해 보시기 바랍니다. 

 

볼록렌즈에 의한 빛의 굴절

 

아마 제 기억이 맞다면, 볼록렌즈와 오목렌즈에 의한 빛의 굴절은 초등학교 시절 처음 배웠던 것 같습니다. 교과서에서도 배웠고, 특히 돋보기를 이용하여 햇빛을 한 곳에 집중 시켜서 종이나 낙엽을 태우는 놀이를 하곤 했습니다. 그 놀이의 근원이 있는 물리가 바로 볼록렌즈에 의한 빛의 굴절, 조금 더 구체적으로 말하면 볼록렌즈에 의한 빛의 집중입니다. 

 

볼록렌즈에 의한 빛의 굴절을 수치해법으로 풀기 위해서는 볼록렌즈에 의해서 공간의 굴절률이 어떻게 주어지는지를 모델링 해야 합니다. 이전 포스팅에서 굴절률이 다른 두 물질의 접합은 단순히 $y=0$을 기준으로 $y>0$에서는 굴절률이 $n_1$, $y<0$에서는 굴절률이 $n_2$와 같이 간단하게 모델링 할 수 있지만, 볼록렌즈는 별다른 대칭성이 없기 때문에 이를 표현하는 것이 직관적이거나 쉽지많은 않습니다. 

 

매우 극단적으로 생긴 볼록렌즈를 생각하면 원 모양의 렌즈 입니다. 

 

원 모양의 렌즈를 만든다면, 위치에 따른 굴절률 $n(x,y)$는 위와 같을 것 입니다. 여기서 진한 파란색은 굴절률이 높은 곳을, 옅은 하늘색은 상대적으로 굴졀률이 낮은 곳을 뜻 합니다. 위에서는 반지름 $R$이 2인 원 모양의 렌즈에 의한 공간의 굴절률 변화를 모델링 한 것 입니다. $r\le R$ 영역의 굴절률은 유리의 굴절률 $n=1.5$, $r>R$ 영역의 굴절률은 진공(공기)의 굴절률인 1.0을 사용하였습니다. 

 

이전 포스팅에서와 마찬가지로, $n(x,y)$와 $\frac{\partial n}{\partial x}$를 수식으로 쓸 수 있어야 수치해법 코드의 각 부분에 수식을 입력할 수 있습니다. 단순하게

$$n(x,y)=\{\begin{array}{ll}1.5,& \text{if }r>R\\ 1.0,& \text{if }r\le R\end{array}$$

라고 정의한다면, $n(x,y)$를 정의하는데는 매우 편하지만, 이 함수는 $r=R$에서 미분이 불가능하기 때문에 매우 불편합니다. 따라서 $r=R$ 부근에서 굴절률이 부드럽게 변하는 함수의 형태를 사용해야 합니다. 지난 포스팅에서와 같이 $tanh$ 함수를 이용하여 불연속 함수를 표현하겠습니다. 그러면, 

$$n(r)=1.0+0.5(\frac{1-\tanh (\frac{r-R}{\sigma })}{2})$$

와 같은 함수를 사용할 수 있습니다. $n(r)$는 $r>R$ 에서는 굴절률이 1.0, $r<R$ 에서는 1.5의 값을 갖고, $r=R$ 부근에서 미분가능하도록 부드럽게 굴절률이 변합니다. 

$\sigma =1.0$ 인 경우의 공간에 따른 굴절률을 시각화 한 것 입니다. 원점에서 굴절률은 1.5이고 원점에서 멀리 떨러진 곳의 굴절률은 1.0 입니다. 불연속적인 굴절률 모델링과 비교했을 때, 이 모델링은 $r=R$ 부근에서 부드럽게 변합니다. 실제로는 $\sigma =0.1$과 같이 작은 값을 사용해 주어야 굴절률이 급격하게 바뀌는 효과를 줄 수 있습니다. 

 

(렌즈를 옆에서 봤을 때) 볼록렌즈는 이렇게 까지 원의 형태는 아니고 위-아래 방향으로 훨씬 긴 타원형 모양입니다. 조금 더 정확히는 타원형에 가깝기 보다는 위-아래로 갈수록 더 뾰족해 지는 모양인데, 원호를 두개 붙인 모양입니다. 원호를 두개 붙인 모양은 기하학적으로 모델링을 하기가 어렵기 때문에 보다 쉬운 타원형을 생각하도록 하겠습니다. 타원형은 원의 방정식에서 $x\to \frac{x}{a},y\to \frac{y}{b}$와 같이 $x,y$축으로의 스케일을 변화한 것 입니다. 이 방법에 따라서 $a=\frac{1}{2},b=3$을 택하면, 

위 그림과 같이 실제 볼록렌즈와 가까운 형태의 모양을 만들 수 있습니다. 볼록렌즈의 역할을 하고 있는 타원 안의 굴절률이 유리의 굴절률인 1.5, 그 밖이 공기의 역할을 하고 있는 굴절률이 1.0인 영역입니다. 위에서 설명한 대로 위치에 따른 굴절률 $n(x,y)$를 해석함수로 쓸 수 있기 때문에 수치해법 코트 작성과 계산이 매우 간단해 집니다. 이제 굴절률 모델링을 마쳤으니, 이 굴절률에 대해서 Eikonal 방정식을 풀어서, 실제 빛의 진행 경로를 시각화 하도록 하겠습니다. 

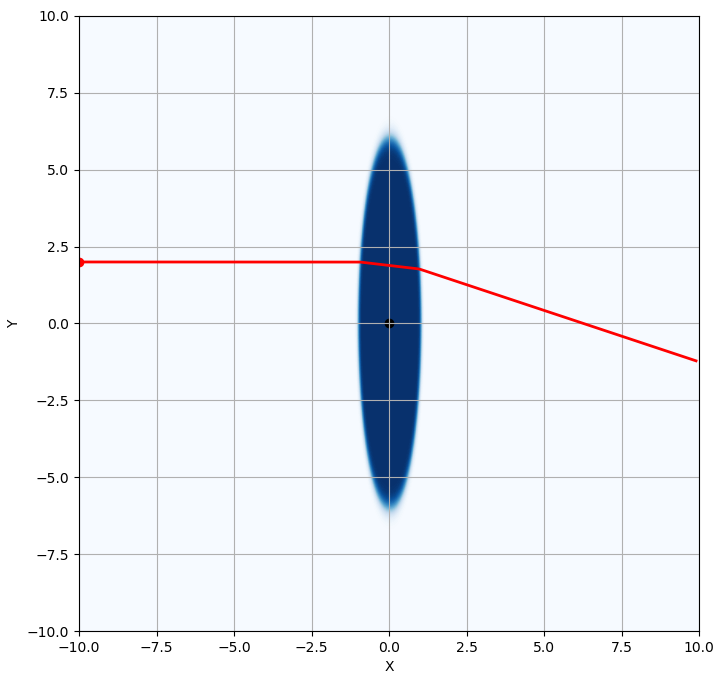
가장 대표적인 볼록렌즈에 의한 빛의 굴절 경로입니다. $(-10,2)$에서 $x$축과 나란한 방향으로 입사한 빛의 경로를 수치해법을 통해 얻었습니다. 빛은 공기에서 유리로 입사할 때, 그리고 유리에서 공기로 다시 나올 때 두번 굴절하게 되는데, 빛이 굴절하는 지점에서 공기와 유리사이의 접선을 생각하면, 국소적으로 봤을 때, 빛의 굴절은 스넬의 법칙에 의해서 설명 됩니다. 

 

빛이 입사하는 높이 ($y$의 초기값)에 따라서 빛이 굴절하는 양상은 당연히 조금씩 다릅니다. 

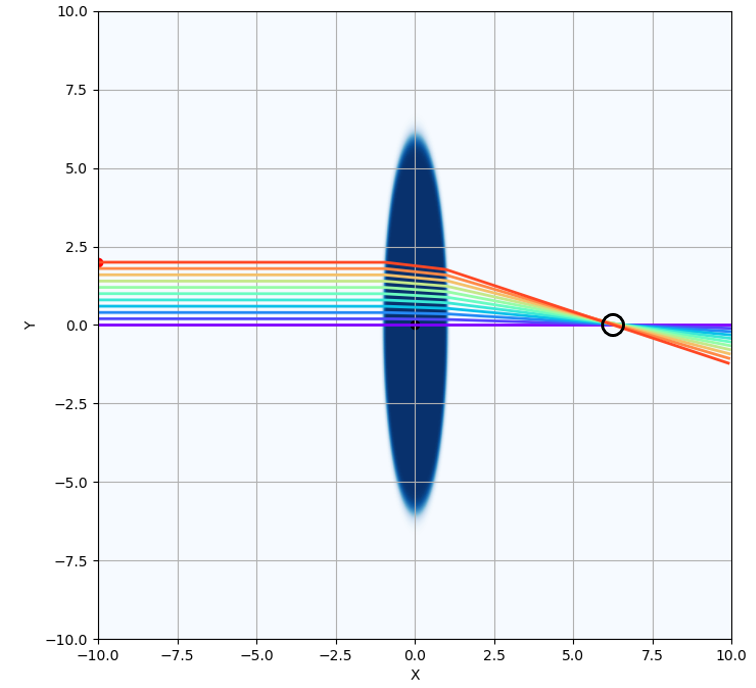
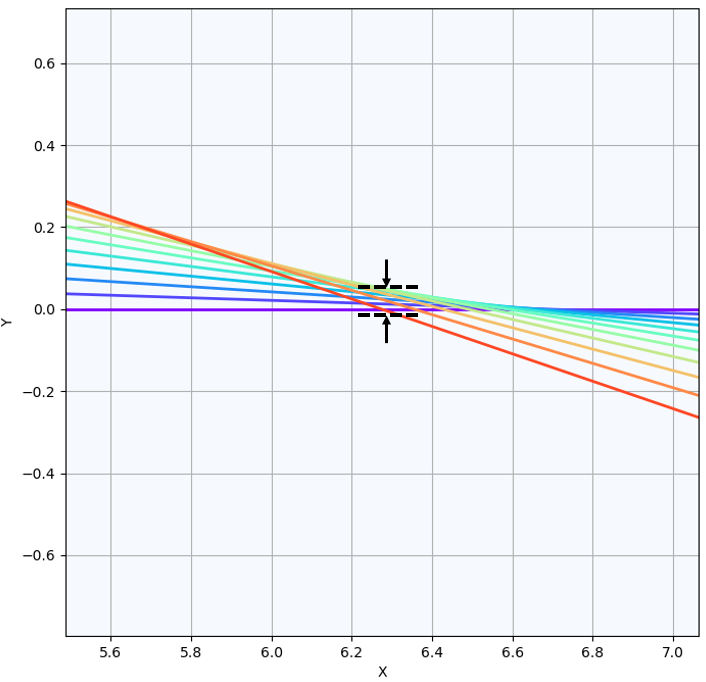
위 결과는 서로 다른 $y$ 초기 위치에서 입사한 빛의 경로를 보여줍니다. $y$의 값에 따라서 빛이 경로를 무지개색으로 표현하였는데, 이는 $y$의 초기값이 서로 다르다는 것을 의미하는 것이지 실제 빛의 색(빛의 파장)을 의미하는 것은 아닙니다. 헷갈리지 마세요. 

 

나란하게 입사한 빛은 $x=6.3$ 부근에서 하나로 합쳐지게 됩니다. 즉 이 곳이 바로 우리가 모델링한 볼록렌즈의 초점거리가 되는 것 입니다. 

$x=6.3$ 부근을 확대해서 보면 모든 빛의 경로가 정확히 한 점에서 보이는 것은 아닙니다. 대략 $\mathrm{\Delta }y=0.1$ 정도의 범위에 빛이 모이게 됩니다. 렌즈의 모양과 굴절률을 매우 단순하게 모델링 하였기 때문에, 나타나는 현상입니다. 렌즈의 중심축($y=0$)으로 부터 떨어진 높이에 상관 없이 모든 빛이 정확히 한 곳에서 모이게 하기 위해서는 매우 세심하게 렌즈 모양을 디자인해야 할 것 입니다. 빛은 렌즈의 중심축을 중심으로 반지름이 $2$인 원에 수직하게 입사하였는데, 렌즈를 통과하고 나서는 반지름이 $0.1$인 원에 모였습니다. 원의 넓이가 $4\pi$에서 $0.01\pi$로 $\frac{1}{400}$으로 줄었습니다. 따라서 빛의 세기는 $400$배 증가하였습니다. 돋보기를 이용하여 신문지를 태우거나 낙엽을 태울 수 있는 원리가 바로 이것입니다. 

 

물방울에 의한 빛의 굴절

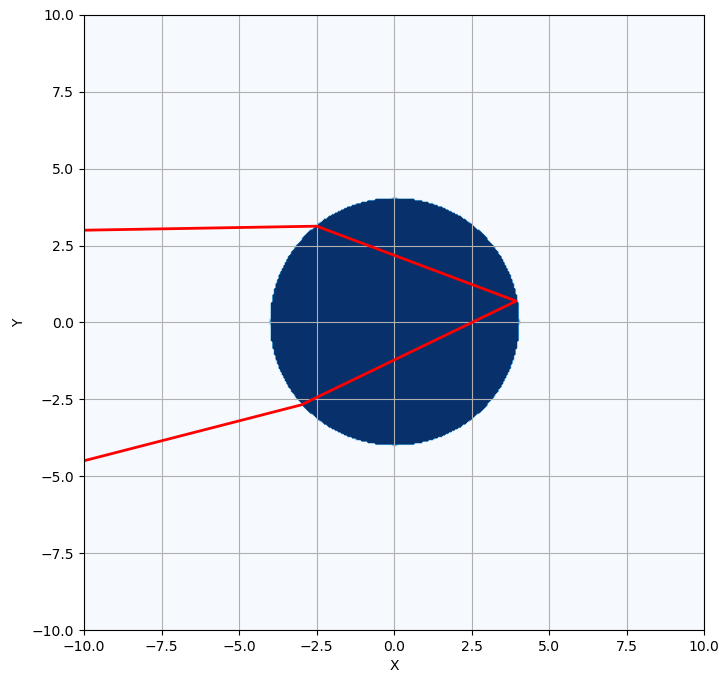
이번에는 물방울에 의한 빛의 굴절을 생각해 보겠습니다. 물의 굴절률은 $1.333$ 입니다. 물방울은 관전한 구 모양으로 가정하겠습니다. 우리는 2차원 물체를 다루고 있으니, 정확한 원 모양입니다. 물방울의 반지름이 $R=4$ 일때, $(-10,3)$ 에서 $x$축 방향으로 입사한 빛의 궤적입니다. 렌즈에서와는 달리 빛은 불방울 내부에서 한 번 전반사를 하게 됩니다. 따라서 빛은 오른쪽($x>0$ 영역)으로 나가지 못 하고, 다시 $x<0$ 영역으로 반대로 나아가게 됩니다. 물방울의 오른쪽 면에서 전반사를 하는 것은 항상 일어나는 것은 아니고, 물방울에서 공기중으로 입사할 때, 입사각이 임계각 보다 큰 경우에만 일어나는 현상입니다. 위에서 사용한 조건이 바로 그 경우에 해당 되는 것 입니다. 

 

물의 굴절률은 빛의 파장에 따라서 약간씩 다른데, 따라서 입사하는 빛의 색에 따라서 빛의 경로가 약간씩 달라지게 됩니다. 이 같은 이유 때문에 백색광, 모든 색을 담고 있는 빛,이 공기중에서 물방울을 만나서 위와 같이 굴절과 반사를 거치게 되면, 백색광은 빨주노초파남보 무지개색으로 갈라지게 되고, 사람이 그 빛을 보게 된다면 무지개로 인식하게 됩니다. Eikonal 방정식을 수치해법으로 풀면 무지개의 현상도 구현할 수 있습니다. (실제로 빛의 파장에 따른 굴절률의 차이는 그리 크지 않고, 간단한 수치해법 코드에서 물방울에 의한 굴절률을 정밀하게 표현하기가 어렵기 때문에, 지금 만든 수치해법 코드에서는 무지개와 같은 해를 얻기는 어려웠습니다)

 

"일반화된" 구형 렌즈

 

이번에는 조금 더 재미난(?) 경우를 생각해 보겠습니다. 위 두 경우에서는 서로 다른 두 물질을 생각했습니다. 렌즈의 경우에는 유리-공기(진공)을 생각했고, 물방울의 경우에는 물-공기(진공)을 생각했습니다. 그리고 공간은 두 부분(물질의 안과 밖)으로 정확히 나뉘어졌습니다. 위치에 따른 굴절률의 변화를 칼 같이 불연속적으로 하고 싶은데, 그 경우 위치에 따른 굴절률의 미분이 불가능하기 때문에 계산의 편의를 위해서 (짧은 영역에서) 부드럽게 변하는 굴절률의 식을 사용했습니다. 

 

이번에는 위치에 따라서 굴절률이 보다 일번적으로 정의된 경우를 생각해보겠습니다. 두 부분으로 나뉘는 것이 아니라 굴절률이 공간 전체에서 부드럽게 변하는 경우 입니다. 

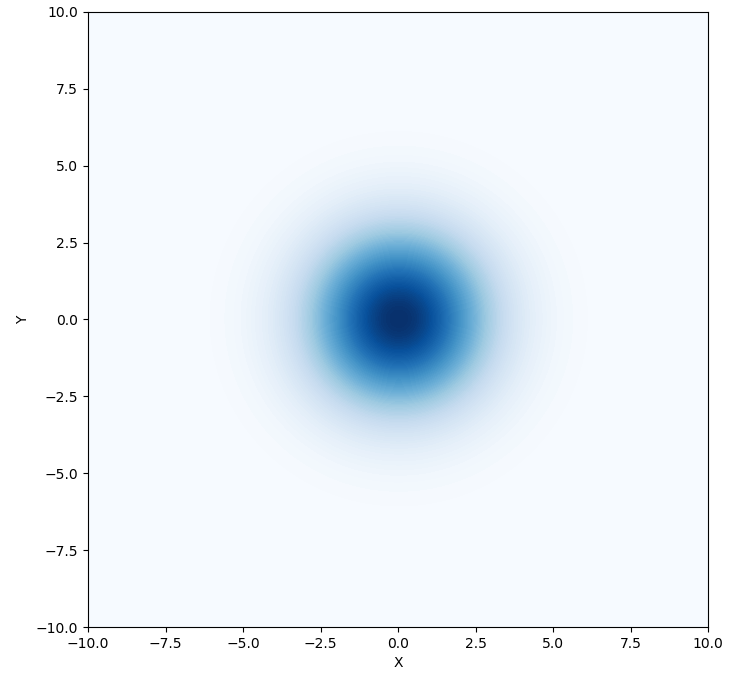
위와 같은 굴절률 $n(x,y)$를 생각해보도록 하겠습니다. 푸른색이 굴절률이 큰 부분(가장 큰 부분은 3), 옅은 하늘색이 굴절률이 가장 작은 부분(가장 작은 부분은 1) 입니다. 원점에서 회전 대칭으로 분포하고 있으며, 원점에서 멀어질수록 굴절률이 작아 집니다. 수식으로 표현하면 $n(x,y)=n(r,\theta )=1+e^{-\frac{1}{2}\frac{r^2}{{\sigma }^2}}$ 를 사용하였습니다. 여기서 $\sigma =2$ 입니다. 정규 분포에서 나오는 바로 그 개형의 함수 입니다. 위 함수를 $r$에 대해서 그리면, 

 

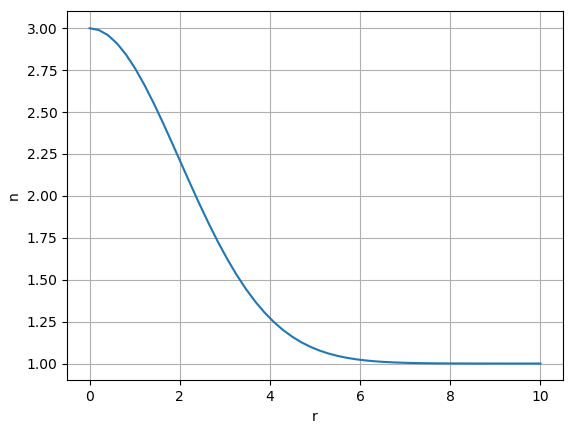
와 같습니다. 이제 이 모양의 "렌즈"에 $x$축에 나란한 방향으로 빛을 입사 시켜 보겠습니다. 

$x=10$에서 서로 다른 $y$값에서 $x$축 방향으로 빛을 입사시켰습니다.

 

$y=0$에서 시작한 빛은 대칭성 때문에 직진합니다. 물론 위치에 따라서 빛의 속도는 달라집니다. 

 

$y>0$에서 시작한 빛은 원점 근처의 높은 굴절률로 인해서 원점 방향인 $-y$축 방향으로 휘게 됩니다. 특히, $y=5$에서 시작한 금색 빛의 굴절 정도기 심한데, 원점을 한 바퀴 돌고 나서 $x$축과 이루는 각도가 약 60도 방향인 곳으로 나아가게 됩니다. $y=4$에서 출발한 연두색 빛 역시 굴절의 정도가 심한데, $-x$ 방향으로 나아갑니다. 초기의 진행 방향과는 완전히 바뀐 방향입니다. 공간상에 굴절률이 다른 부분이 있으면 빛의 경로는 이와 같이 급격하게 바뀌게 됩니다. 

 

$y=4.187$ 에서 $-x$축 방향으로 입사한 빛은 원점을 한 바퀴 돌고 나서 완전 바내 방향인 $-x$축 방향으로 되돌아 갑니다. 거울이 없는데도 불구하고 마치 거울이 있는 것 처럼 빛이 완전히 반대 방향으로 진행하게 되는 것 입니다. 또 다르게 설명하면 $y=-4.2$ 부분에 있는 사람이 $+x$축 방향을 바라 본다면, 바로 옆에 있는 $y=4.187$에 위치한 사람을 볼 수 있는 것 입니다. 

 

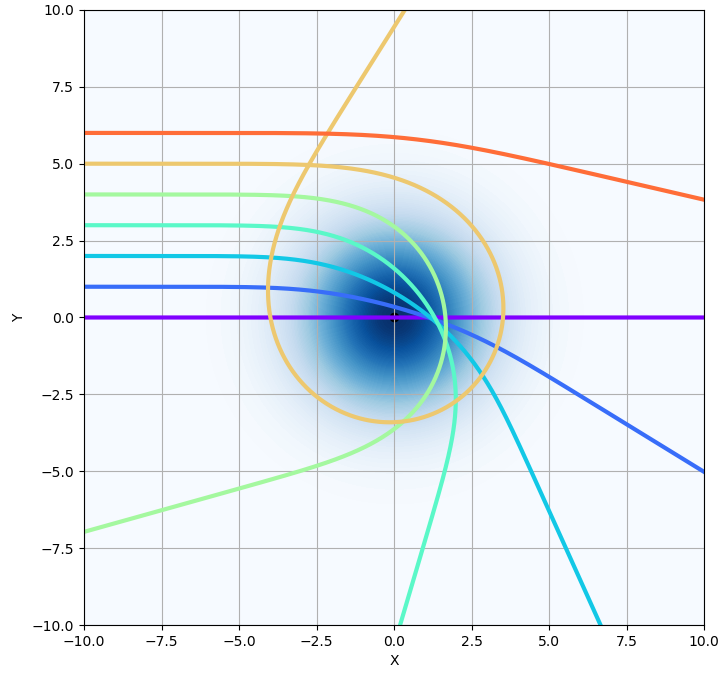
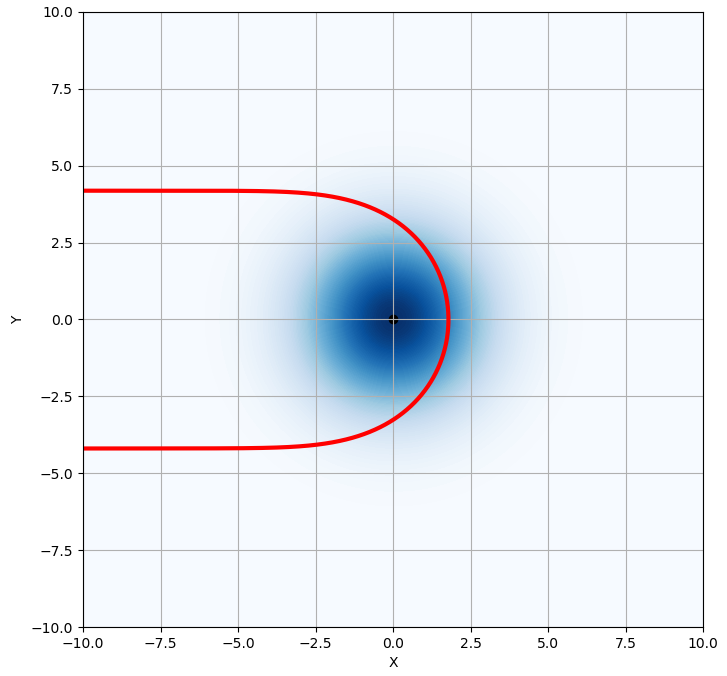
신기루 현상

 

조금 다른 공간에 따른 굴절률 모델을 생각해 보겠습니다. 이번에 생각할 굴절률 모델은 $y$값이 커질수록 굴절률이 커지는 케이스 입니다. 수식으로 표현하면

$$n(x,y)=n(y)=n_0+\kappa y$$

와 같은 형태입니다. 여기서 $n_0,\kappa$는 물성을 기술하는 파라미터 입니다. 위와 같이 정의한 굴절률 하에서, 위의 예제에서와 같이 $(-10,10)$의 위치에서 다양한 방향으로 빛을 쏘았을 때, 빛의 경로를 계산해 보도록 하겠습니다. 

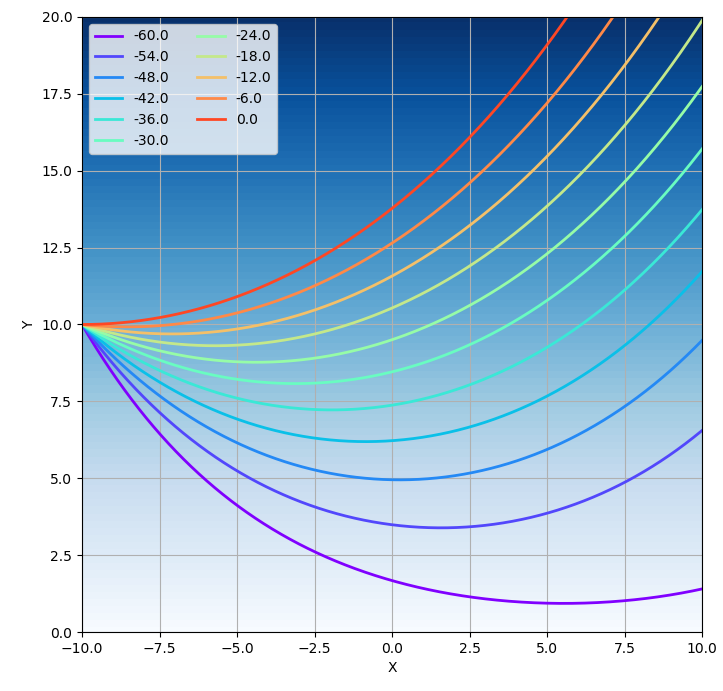
결과는 위와 같습니다. 배경에 나온 옅은/진한 파란색은 물질의 굴절률을 나타냅니다. (이전의 경우와 같이) 파란색의 진하기가 짙을 수록 굴절률이 큰 곳을 의미 합니다. 실제 계산에서는 $n_0=1,\kappa =1.3$의 값을 선택하였습니다. 특별한 이유는 없고, 결과를 정성적으로 잘 보여주는 값을 선택했습니다. 초기 빛의 진행 방향을 $\theta =-\frac{\pi }{3}\sim 0$ 로 하여 계산하였습니다. 

 

오른쪽 아래로 나아가던 빛은 얼마 진행한 뒤 방향을 틀어 오른쪽 위로 진행합니다. 

 

이 문제는 수치해법으로 답을 찾기 전에 정성적인 방법으로 빛의 경로를 예측할 수 있습니다. 물질의 굴절률은 $y$값에 따라서 연속적으로 바뀌지만 개념적으로는 $y$값에 따라서 불연속적인 굴절률을 갖는 매우 얇은 물질들이 켜켜이 쌓여 있는 것이라 생각할 수 있습니다. 바로 아래 그림과 같이 생각할 수 있습니다. 

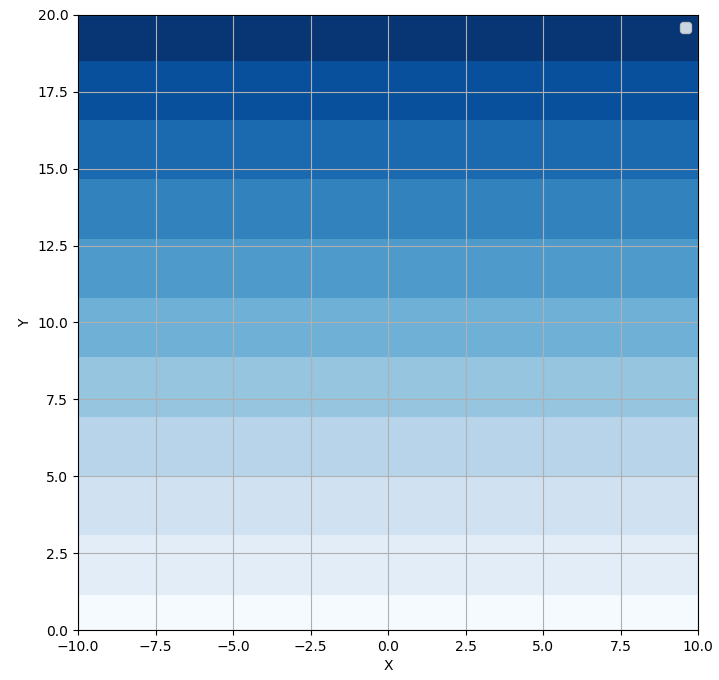
이와 같은 굴절률 배치라면, 특정 영역에서 그 위 혹은 아래 영역으로 진행하는 것은 단순히 굴절률이 다른 두 물질 사이에 굴절이기 때문에, 스넬의 법칙을 적용하여 빛의 경로(빛의 진행 각도)를 알 수 있습니다. 따라서 스넬의 법칙을 여러번 적용하면 빛이 진행하는 경로(선분의 합)을 알 수 있고, 굴절률이 같은 영역의 두께 ($y$축 방향의 거리)가 무한히 짧은 극한을 생각한다면 Eikonal 방정식의 해의 경로가 됩니다. 

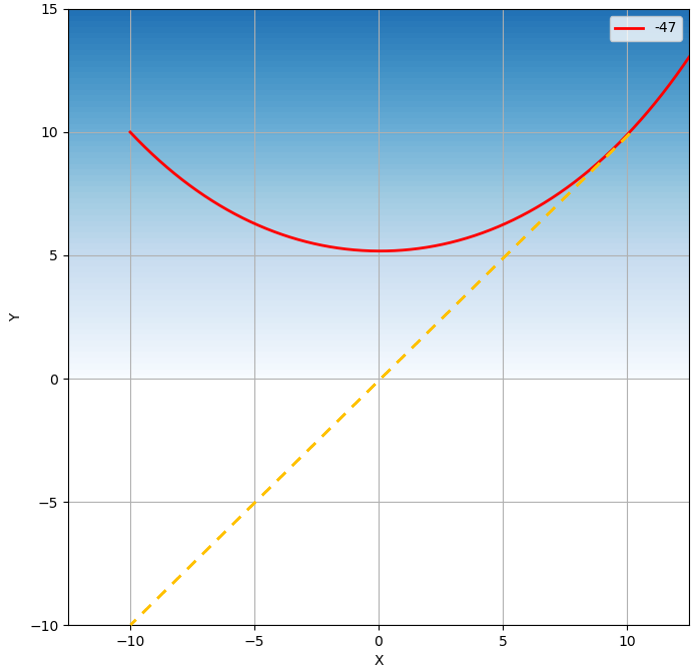
특정한 입사 각도를 생각해 보겠습니다. 만일 초기 빛의 진행 각도가 $-47$도였다면, 빛의 경로는 위 그림과 같을 것 입니다. $(-10,10)$에서 시작한 빛은 $(10,10)$에 도달합니다. 대칭성에 따라서 $(10,10)$에 도달할 때 빛의 진행 각도는 $+47$도가 됩니다. 만일 $(10,10)$의 위치에 관찰자가 있다면 이 관찰자는 빛의 초기 위치가 $(-10,10)$이라고 생각하기 보다는 빛은 노란색으로 표시한 경로를 따라서 진행한 것으로 보일 것 입니다. 

 

이 같은 굴절률에 대한 빛의 경로는 신기루 현상의 원인입니다. 만일 $x=-10$ 지점에 나무가 한 그루 서 있었다면, 

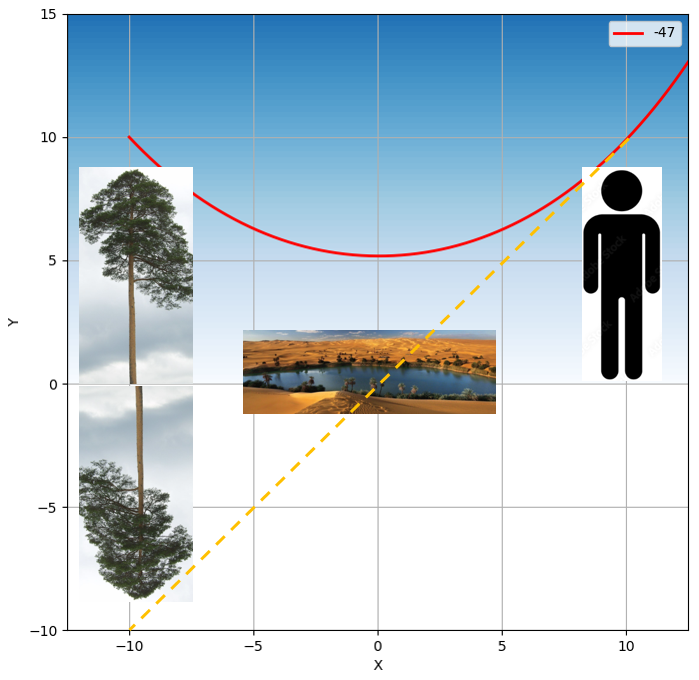
빛의 굴절에 의해서 $x=10$의 관찰자가 보는 나무의 방향은 정상적인 방향이 아니라 바로 위 그림에서와 같이 위와 아래가 바뀐 방향일 것 입니다. 관찰자는 나무가 거꾸로 서 있는 것은 물에 비쳐 반사된 것으로 생각하게 되고, 따라서 나무와 관찰자 사이에 오아시스가 있을 것이라고 착각하게 됩니다. 사막에서 공기의 온도는 지표면 근처가 높고, 고도가 올라가면 낮아 집니다. 공기의 온도가 높아지면 공기의 밀도가 낮아지게 되고, 이 경우 굴절률은 더 낮아 집니다. 따라서 이 문제에서의 가정과 같이 사막의 표면 근처에서는 고도($y$방향)가 높아질 수록 상대적으로 공기의 굴절률이 높아지게 됩니다. 물론 실제 측정값(물리상수)는 위 수치해법에서 사용한 $n_0,\kappa$의 값과는 다를 것 입니다. 수치해법에서는 해(빛의 진행 경로)의 정량적인 성질을 잘 보여 줄 수 있는 임의의 값을 사용하였습니다.