슈뢰딩거 방정식
학부 물리학 전공 양자역학 과목에서는 주로 고전역학과 비교되는 양자역학의 특징, 양자역학의 형식적인(수학적인) 구조, 시간에 의존하지 않는 슈뢰딩거 방정식의 풀이법을 주로 배웁니다. 슈뢰딩거 방정식이라 하면,
$$i \hbar \frac{\partial \Psi}{\partial t}(x,t) = \hat{H}\Psi(x,t)$$
를 의미하지만, 학부 양자역학의 대부분의 문제에서는 시간에 의존하지 않는 해밀토니안을 다루기 때문에, 시간에 의존하지 않는 슈뢰딩거 방정식인,
$$\hat{H}\psi(x) = -\frac{\hbar^2}{2m}\frac{d^2}{dx^2}\psi(x) + V(x) \psi(x) = E\psi(x)$$
를 슈뢰딩거 방정식으로 이해하고 문제를 풀기도 합니다. 학부 수준에서는 기본적인 양자역학의 특징과 형식적인 성질을 공부하는 것도 어렵기 때문에, 시간에 의존하는 해밀토니안에 대해서 다루거나 혹은 시간에 의존하지 않는 해밀토니안이라고 하더라도 파동함수의 시간에 따른 변화를 다루지는 않는 것이 일반적입니다.
물론, 시간에 따른 파동함수의 변화를 다루지 않는 것은 아닌데, 대부분의 경우에는 "$t = 0$에서 파동함수가 $\psi(x) = \sum_{n=1}^{\infty} c_n \phi(x)$ 로 주어질 때(여기서 $\phi(x)$는 고유 함수), 임의의 시간 $t$에서 파동함수는
$$\psi(x,t) = \sum_{n=1}^{\infty} c_n e^{-\frac{iE_nt}{\hbar}} \phi(x)$$
로 주어진다." 정도만 배우고 넘어갑니다. 저 역시 기억을 더듬어 거슬러 올라가면, 물론 매우 오래된 과거이긴 하지만, 이 정도가 전부였던것 같습니다. 물론 강의를 하는 교수님은 이것보다 더 많은 것을 가르쳐주셨을수도 있지만, 제가 현재 기억하고 있는 바는 이 정도가 전부입니다. 물론 형식적으로 볼 때, 이 정도가 어쩌면 전부라고 할 수 도 있겠지만, 단순히 원리를 알고 있는 것과, 이를 구체적인 문제에 적용하여 풀어 보고 그 해를 구하는 것은 조금은 다른 문제 입니다.
이번 포스팅에서는 구체적인 문제에서 파동함수의 사간에 따른 변화를 구해보고 이를 그래프와 애니메이션을 통해서 시각화 해 보도록 하겠습니다. 아직 양자역학을 배운지 얼마 안된 분이거나, 혹은 양자역학을 배운지 조금 되었다고 하더라도 시간에 따른 파동함수의 변화가 구체적으로 어떻게 되는지에 대해서는 한 번도 못 본 분도 많을 것이라 생각합니다. 시간에 따른 파동함수의 변화를 구하는 두가지 방법을 소개하고, 양자역학에서 자주 등장하는 문제에서 시간에 따른 파동함수이 변화가 어떻게 되는지를 직접 시각화 해보도록 하겠습니다. 시간에 따른 파동함수의 변화에 대해서 처음 다루는 포스팅인 만큼, 이번 포스팅에서 등장하는 해밀토니안은 모두 시간에 의존하지 않는 해밀토니안으로 한정하도록 하겠습니다. 또한 시각와 계산의 편의를 위해서 공간 차원은 1차원으로 한정하겠습니다. 아래에서 설명하는 방법은 임의의 차원으로 일반화 할 수 있습니다.
방법 1 : 고유 함수를 이용하는 방법
첫 번째 방법은 이미 앞에서 설명하였는데, 슈뢰딩거 방정식의 선형성을 이용하는 것 입니다. 특정 시간 (별다른 언급이 없다면 특정 시간은 $t=0$을 의미 합니다)에서 파동함수 $\psi(x)$를 알고 있다면, 이를 해밀토니안의 고유 함수를 통해 분해하고, 각 고유 함수의 시간에 따른 변화를 계산 한 뒤, 다시 더하는 방법입니다. $\phi_n(x), E_n$가 해밀토니안의 고유 함수와 고유 에너지라고 한다면,
$$\phi_n(x,t) = e^{-\frac{iE_nt}{\hbar}}\phi_n(x,0)$$
은 시간에 의존하는 슈뢰딩거 방정식의 해가 됩니다. 따라서,
$$\psi(x, 0) = \sum_{n=1}^{\infty} c_n\phi_n(x, 0)$$
와 같이 $t=0$에서 $\psi(x,0)$이 $\phi_n(x,0)$의 합으로 쓰여진다면, 시간에 의존하는 슈뢰딩거 방정식의 선형성에 따라서, 자연스럽게
$$\psi(x,t) = \sum_{n=1}^{\infty} c_n\phi_n(x, t) = \sum_{n=1}^{\infty} c_n\phi_n(x, 0)e^{-\frac{iE_nt}{\hbar}}$$
가 됩니다. 따라서 이 방법을 이용하기 위해서는
(1) 주어진 해밀토니안의 고유 함수, 고유 에너지를 구하기
(2) $\psi(x,0)$에 대응되는 $c_n$구하기
를 해야 합니다. 여기서 $c_n = \langle \phi_n | \psi \rangle$으로 구체적으로 쓴다면,
$$c_n = \int \phi_n(x)^* \psi(x) dx$$
입니다. 이 두 과정은 학부 양자역학 시간에 많이 해 봤을것이라 생각합니다. 그러나, 매우 특수한 경우를 제외하고는 해석적인 방법으로 위 식을 적분하여 $c_n$을 얻은 것은 불가능합니다. 따라서 학부과정에서는 보통 $c_n$을 위 식으로 쓰는 것에서 논의를 마쳤습니다. 따라서 $c_n$의 값을 얻기 위해서는 컴퓨터를 이용한 수치해법을 사용해야 하며, 또한 $\sum_{n=1}^{\infty}$와 같이 합을 구하는 과정 역시 수치해법을 사용하여 계산해야 합니다.
방법 2 : 시간에 의존하는 슈뢰딩거 방정식을 바로 푸는 방법
방법 1은 슈뢰딩거 방정식의 수학적인 성질인 선형성을 이용하여 문제는 간단하게 푸는 방법입니다. 이번에 소개할 방법은 그런 것을 사용하지 않고, 곧이 곧대로 편미분방정식을 푸는 것입니다. 수치해법으로 통해서 (편)미분 방정식을 푸는 것은 이미 이전 포스팅에서 여러번 소개하였는데, 기본적인 방법은 연속적인 값을 갖는 시간과 공간의 값을 불연속화 하는 것 입니다. 즉 실수의 값을 갖는 시간 $t$를 매우 작은 간격 $\Delta t$ 단위로 분할하고 $t = n\Delta t$의 관계를 통해서 시간을 정수 $n$으로 대응시키는 것 입니다. 공간 역시 마찬가지 방법을 통해서 $x = m \Delta x$의 관계를 통해서 대응 시킵니다. 이를 통해서 $(x, t) \rightarrow (m, n)$으로 대응이되고, $\psi(x,t) \rightarrow \psi(m,n)$이 됩니다. 또한 $\psi(x, t)$에 대한 편미분 방정식을 $psi(m,n)$에 대한 분차방정식으로 바꾼뒤 문제를 풀게 됩니다. 이 방법에 대해서는 이미 이전 포스팅에서 설명한 바 있으니, 이 방법에 익숙하지 않으신 분은 이전 포스팅을 읽은 후, 뒷 부분을 보는것이 좋습니다.
https://studyingrabbit.tistory.com/37?category=911605
유한요소법(Finite Element Method)으로 미분 방정식(헬름홀츠 방정식) 풀기
미분방정식은 응용수학, 물리학, 공학에서 가장 많이 나오는 수학적 문제입니다. 특히나 물리학과 공학에서는 미분 방정식이 거의 전부라고 해도 좋을 정도로 미분 방정식은 지배적인 문제입니
studyingrabbit.tistory.com
유한요소법에서는 파동함수 $\psi(x)$를 $\psi_n$으로 수열처럼 표현합니다. 여기서 아랫첨자 $n$은 $n$번째 고유함수를 나타내는 의미로 쓰인 것이 아니라, $x = n \Delta x$의 의미로 쓰인 것 입니다. 즉 $\psi_n = \psi(x_n = n \Delta x)$입니다. 슈뢰딩거 방정식에서는 $x$의 2계 미분 연산자가 등장하는데, 이를 $\psi_n$으로 쓰면,
$$\frac{d^2}{dx^2} \psi(x) \approx \frac{\psi_{n+1} - \psi_n + \psi_{n-1}}{\Delta x^2}$$
이 됩니다. 이를 이용하여 $\hat{H} \psi(x)$를 같은 방식으로 표현하면,
$$-\frac{1}{2}\frac{\psi_{n+1} - \psi_n + \psi_{n-1}}{\Delta x^2} + V_n \psi_n$$
이 됩니다. 여기서 $\hbar, m$와 같은 상수들은 모두 $1$로 취급하였고, $V_n = V(x_n = n \Delta x)$를 의미 합니다. 파동함수의 시간에 대한 미분 역시 마찬가지로 쓸 수 있는데,
$$\frac{\partial \psi}{\partial t} \approx \frac{\psi_{n+1} - \psi_n}{\Delta t}$$
입니다. 여기서 $\psi_n = \psi(t_n = n \Delta t)$ 입니다. 위 두 식을 이용하여 시간에 의존하는 슈뢰딩거 방정식을 $\psi(n,m) = \psi(x_n, t_m) = \psi(n \Delta x, m \Delta t)$를 이용한 식으로 표현하면,
$$i \frac{\psi(n, m+1) - \psi(n, m)}{\Delta t} = -\frac{1}{2}\frac{\psi(n+1, m) - \psi(n,m) + \psi(n-1, m)}{\Delta x^2} + V_n \psi(n, m)$$
가 됩니다. $t=0$에서의 초기 조건 $\psi(n,0)$이 주어졌을 때, 위 식을 이용하여 임의의 $m \gt 0$에 대해서 $\psi(n,m)$를 구할 수 있습니다. 예를들어, $\psi(m,1)$은 위 식에 따라 바로
$$\psi(n,1) = \psi(n,0) + \frac{\Delta t}{i} \Big( -\frac{1}{2}\frac{\psi(n+1, 0) - \psi(n,0) + \psi(n-1, 0)}{\Delta x^2} + V_n \psi(n, 0) \Big)$$
이 됩니다. $\psi(n,0)$에 대한 정보가 있다면, $\psi(n,1)$를 구할 수 있는 것이죠. 물론 개념적으로는 이렇게 계산할 수 있고, 실제로 빠르고 정확한 계산을 위해서는 조금 더 복잡한 수치해법의 테크닉을 이용합니다.
방법 2는 앞서 설명한 바와 같이, 이 방법은 슈뢰딩거 방정식이 수학적인 특성을 전혀 사용하지 않고, 단순히 매우 일반적으로 사용 될 수 있는 방법입니다. 따라서 방법 1과 비교했을 때 뚜렷한 장단점이 존재하는데, 방법 2는 매우 일반적인 조건에서 이용될 수 있습니다. 위치 에너지 $V(x)$의 개형이나 여타 문제의 부대조건과 상관 없이 적용 할 수 있다는 장점이 있습니다. 그러나 문제를 쉽게 풀 수 있는 방법을 전혀 사용하지 않기 때문에, 방법 1에 비해서 계산시간에 더 오래 걸린다는 단점이 있습니다. 문제를 풀 때는 그 때 그 때 조건에 따라서 더 효율적인 방법을 사용하는 것이 좋습니다.
구체적인 문제에서 시간에 따른 파동함수가 어떻게 변화하는지 계산해 보도록 하겠습니다. 다양한 형태의 위치 에너지에 대해서 응용을 하기 위해서는 방법1보다는 방법2가 편하기 때문에, 방법2를 따라서 프로그램을 구성하도록 하겠습니다. 물론 필요에 따라서 방법1로 문제를 푸는 것도 설명하도록 하겠습니다. 그리고 문제에 따라서 위치 에너지와 파동함수 값을 달리하면서 해를 구해 보도록 하겠습니다. 별다른 설명이 없다면, 질량, 디락 상수($\hbar$)와 같은 물리상수는 모두 $1$로 두었습니다. (시간과 공간의 단위는 모두 arb. unit으로 생각하는 것이 편합니다)
상자 속 입자(particle in a box) 문제의 시간에 따른 파동함수의 변화
"상자 속 입자" 문제는 양자역학에서 처음 나오는 예제로 $x \in [-\frac{L}{2}, \frac{L}{2}]$ 영역에 속박된 입자를 양자역학적으로 기술하는 문제입니다. 시간에 무관한 슈뢰딩거 방정식의 해와 해의 성질에 대해서는 독자분들도 너무나도 잘 아실테니 이에 대한 설명은 넘어가도록 하겠습니다.
$t=0$에서 파동함수가
$$\psi(x, 0) = \frac{1}{\sqrt{2 \pi \sigma^2}} e^{-\frac{1}{2}\frac{x^2}{\sigma^2}}$$
와 같이 원점을 중심(평균)으로 하고 표준편차가 $\sigma$인 가우스 함수라고 하겠습니다. 이는 고전적인 입자가 원점에 정지에 했는 상태를 표현한다고 볼 수 있습니다. 시간에 의존하는 슈뢰딩거 방정식을 풀어 임의의 시간 $t$에서의 위치에 따른 파동함수를 구하면, 파동함수의 변화는 아래 애니메이션의 결과와 같습니다.
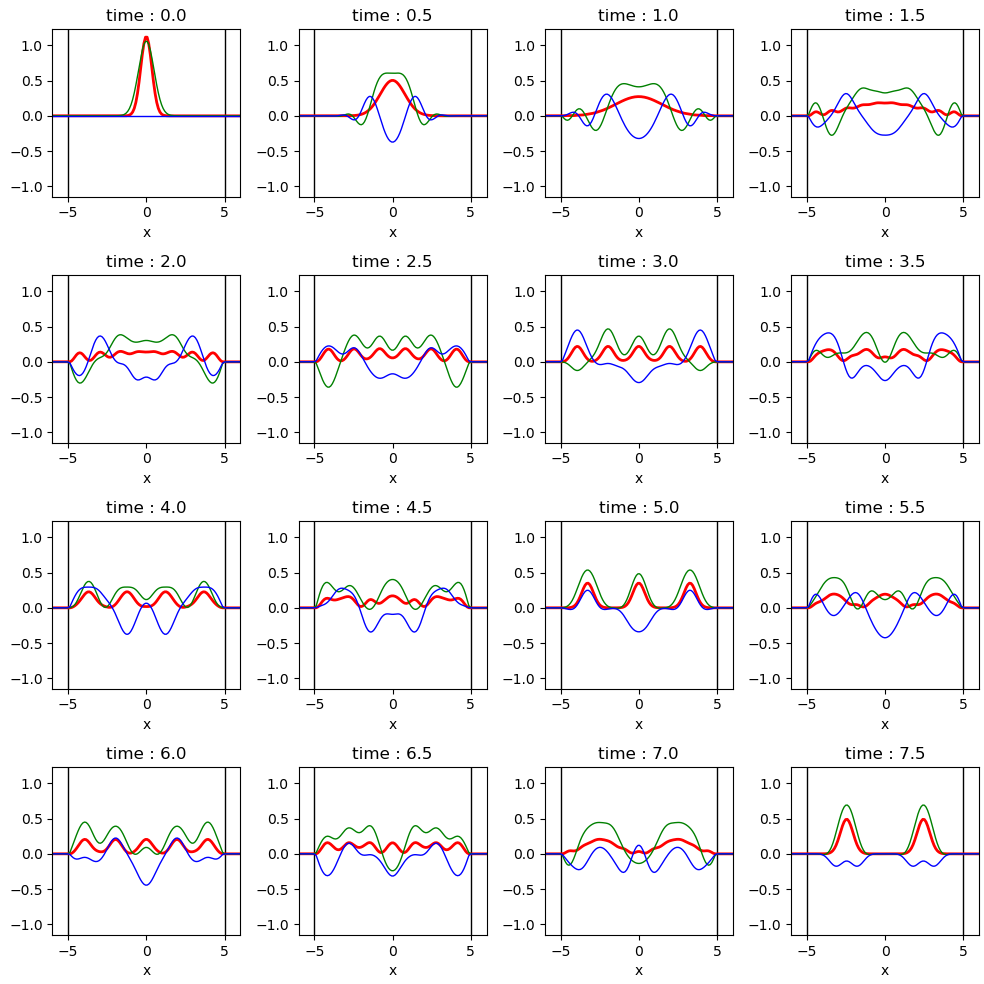
설명을 위해서 각 시간에서의 파동함수와 파동함수의 제곱을 나타내면 위 그래프와 같습니다. 그래프에서 녹색은 파동함수의 실수부, 파란색은 파동함수의 허수부, 빨간색은 파동함수의 크기의 제곱 (실수부 제곱과 허수부 제곱의 합)을 뜻 합니다. 위 계산에서는 $L = 10, \sigma = 1$ 값을 사용하였습니다.
$t = 0$의 파동함수 $\psi(x, 0)$는 상자 속 입자 문제의 고유 상태가 아니기 때문에 시간에 따라서 파동함수의 형태가 달라집니다. 위 스냅샷에서와 같이 시간이 지날수록 파동함수는 넓게 퍼지게 되고, 상자의 벽($x = \pm \frac{L}{2}$)에 파동함수가 도달하게 된다면 반사하게 됩니다. 이후 파동함수는 공간상에 넓게 퍼지게 되고, 마지 정상파와 같은 형태의 모습을 보여줍니다.
시간이 더 지나게 되면 $t = 7.5$에서와 같이 퍼져 있던 파동함수는 가끔씩 특정한 위치에 국소적으로 모이기도 하는데, 이는 각 고유 함수의 고유 에너지가 특정한 비율로 주어지기 때문입니다. 상자 속 입자 문제의 경우 고유 에너지의 크기는 $$E_n \propto n^2$$
로 주어지고, 이에 대응되는 주기는
$$T_n \propto \frac{1}{n^2}$$
으로 주어집니다. 만일 시간 $t$가 몇 몇 고유 함수에 대응되는 주기의 공배수가 될 때, 위 그래프에서 $t=7.5$와 같은 "구조"를 같은 파동함수가 얻어집니다.
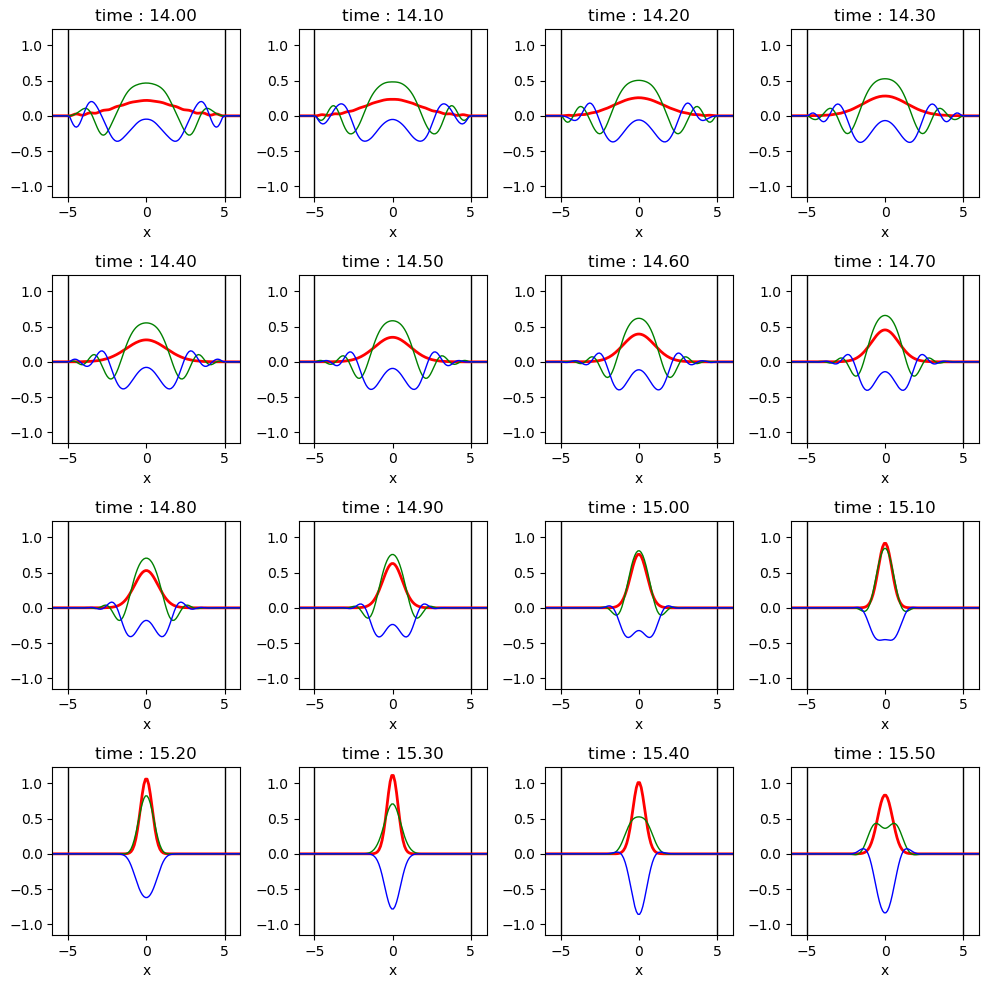
$14 \lt t \lt 15.5$ 에서의 파동함수의 스냅샷 입니다. $t = 15.2$ 의 파동함수의 크기(붉은색 그래프)를 보면 $t=0$에서의 파동함수의 크기와 거의 동일합니다. 이는 앞에서 설명한 것과 같이, $\psi(x,0)$를 구성하는 고유 함수들의 주기의 공배수가 대략 $t = 15.2$ 정도가 되기 때문입니다. 물론 파동함수의 크기만 같을 뿐, 파동함수를 구성하는 실수부, 허수부의 파동함수의 개형은 다릅니다.
처음 양자역학을 배울 때, $\psi(x,t)$를 구해서 애니메이션을 그려 보기 전에는 막연하게 "파동함수는 전체 공간에 균등하게 퍼진다"라고 생각했는데, 실제로는 위 애니메이션과 같이 파동함수는 주기적인 "구조"를 갖게 됩니다.
포텐셜 장벽(potential barrier)에 의한 반사와 투과(양자 터널링)
상자 속 입자 문제 다음으로 학부 양자역학에서 많이 다루는 문제는 1차원 스케터링 문제 입니다. 예를들어
$$\begin{equation}
V(x)=\begin{cases}
V_0 \gt 0, &x \in [x_1, x_2] \\
0, &\text{otherwise}
\end{cases}
\end{equation}$$
와 같은 포테셜이 있을 때, 운동량 고유 함수 $\psi(x) = e^{ikx}$의 입사파에 대한 반사파와 투과파를 계산하는 문제 입니다. 여기서 $x_1 \lt x_2$ 이고 $x_1, x_2$는 원점 근처에 있는 값이라고 하겠습니다. 즉 $x=-\infty$에서 입사한 파동을 기술하는 문제입니다. 하지만 정확히 하자면, 운동량 고유 함수 $\psi(x) = e^{ikx}$는 전공간에 동일한 확률로 퍼져 있는 상태를 기술하고 있기 때문에, $x=-\infty$와 같이 "위치"를 지정할 수 없습니다. 따라서 파동함수가 $x \lt 0$에서 $x \gt 0$ 방향(즉, $+x$ 방향)으로 진행하는 것을 묘사하기 위해서는 파동 묶음 (wave packet)를 생각해야 합니다.
이를 가장 간단하게 표현할 수 있는 파동 묶음은
$$\psi(x,0) = ce^{-\frac{1}{2}\frac{(x-x_0)^2}{\sigma_x^2}} e^{ik_0(x-x_0)} $$
입니다. $|psi(x,0)|$는 평균이 $x = x_0$, 표준편차가 $\sigma_x$인 정규분포 입니다. 여기서 $c$는 파동함수의 정규화를 위한 상수 입니다. ($|\psi(x,0)|$이 아닌 확률 밀도 함수인 $|\psi(x,0)|^2$가 표준편차가 $\sigma_x$인 함수로 만들 수도 있으나, 편의상 $|\psi(x,0)|$ 자체가 이 성질을 만족하도록 두었습니다) $e^{ik_0(x-x_0)}$항은 파동 묶음의 평균 운동량이 $k_0 \gt 0$이 되어 $+x$ 방향으로 진행하는 파동 묶음이 되도록 해 주는 항 입니다. $\psi(x,0)$를 푸리에 변환하여 운동량 공간에서 표현하면,
$$\psi(k,0) = de^{-\frac{1}{2}\frac{(k-k_0)^2}{\sigma_k^2}}$$
이 됩니다. 즉 평균이 $k = k_0$이고 표준 편차가 $\sigma_k$인 정규 분포를 따르는 함수입니다. 여기서 $d$는 파동함수의 정규화를 위한 상수 입니다. 즉, $k = k_0$만 갖는 함수라면 $\psi(x,0) = e^{ik_0x}$가 되는데, $k = k_0$ 뿐 아니라, 그 근방의 운동량 성분이 있다면 파동 묶음이 되어 공간상의 특정한 점에 국소화 될 수 있습니다. 푸리에 변환의 성질에 따라서 $\sigma_x^2 \sigma_k^2 = 1$이 성립합니다. 실공간에서 완전히 퍼저 있는 파동함수($\sigma_x = \infty$)는 운동량 공간에서 특정한 $k$값만 갖게 되며, 반대로 실공간에서 특정한 한 점에 국소화 된 파동함수($\sigma_x = 0$, 즉 $\psi(x,0) = \delta(x)$)는 운동량 공간에서 완전히 퍼진 상태가 됩니다. 위에서 정의한 정규분포 형태의 함수는 실공간과 운동량 공간에서 모두 정규분포의 형태를 취하며, 두 공간에서 적당히 국소화 되게 됩니다.
그러면, $t = 0$에서 $\psi(x,0) = ce^{-\frac{1}{2}\frac{(x-x_0)^2}{\sigma_x^2}} e^{ik_0(x-x_0)}, x_0 \lt 0$의 파동함수가 원점 근처에 존재하는 얇지만 높은 포텐셜 장벽에 출돌하여 반사와 투과를 하는 시뮬레이션을 해 보도록 하겠습니다. 즉, $\psi(x,0)$의 초기 조건에 대한 시간에 의존하는 슈뢰딩거 방정식을 풀어서 $\psi(x,t)$를 구하는 것 입니다.
시뮬레이션 결과는 위와 같습니다. $x = x_0 = -10$에서 국소화 된 파동함수는 $x = 0$을 향해 가고, $x=0$에서 포텐셜 장벽과 부딛히고 난 뒤 일부는 반사를 하고 일부는 투과를 하여 진행합니다. 위 시뮬레이션에서 포텐셜 장벽을 기술하는 파라미터는 $x_0 = 0, x_1 = 0.1, V_0 = 100$입니다.
입사하는 파동 묶음이 포텐셜 장벽에 무딛히지 직전의 시간에 따른 변화 입니다. 위에서와 같이 그래프에서 녹색은 파동함수의 실수부, 파란색은 파동함수의 허수부, 빨간색은 파동함수의 크기의 제곱 (실수부 제곱과 허수부 제곱의 합)을 뜻 합니다. 운동량이 $k$인 파동함수이 고유 에너지는 $\omega = \frac{k^2}{2}$로 파동의 위상속도(phase velocity)와 군속도(group velocity)가 서로 다릅니다. 따라서 초기에 국소화 돼 있던 파동 묶음은 시간이 진행함에 따라, 국소화된 정도가 작아지게 됩니다(시간이 지남에 따라서 실공간상에서 더 넓게 퍼지게 됩니다). 운동량의 평균 $k_0$값은 파동함수가 실공간에서 국소된 영역에서 대략 6번 정도 진동하도록 설계되었습니다.
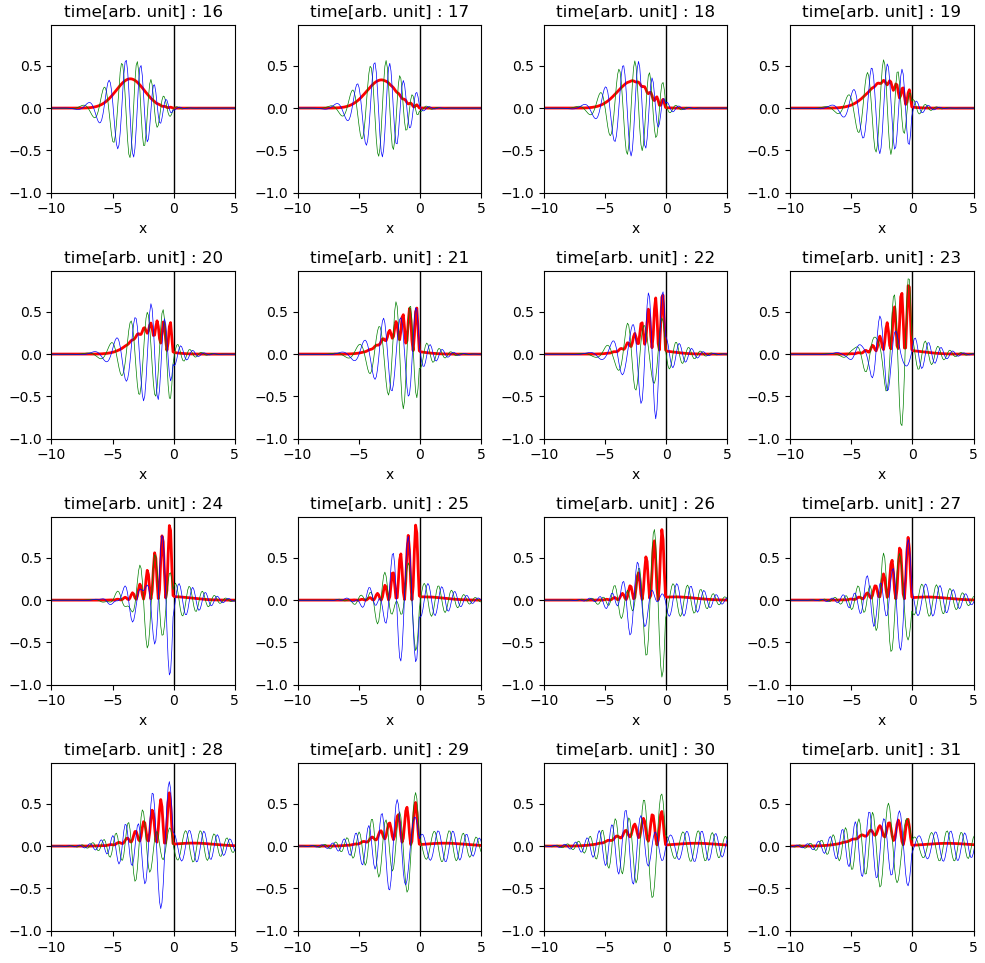
파동 묶음이 $x = 0$에 있는 포텐셜 장벽에 부딛히기 직전 부터 부딛히고 난 뒤 반사, 투과를 하는 시점의 스냅샷입니다. 파동함수에서 함수값이 가장 큰 지점이 원점에 도달할 때 파동함수의 확률 밀도 함수가 공간상에서 매우 급격하게 진동합니다. $t = 25$ 이후에는 반사 혹은 투과를 하게 됩니다.
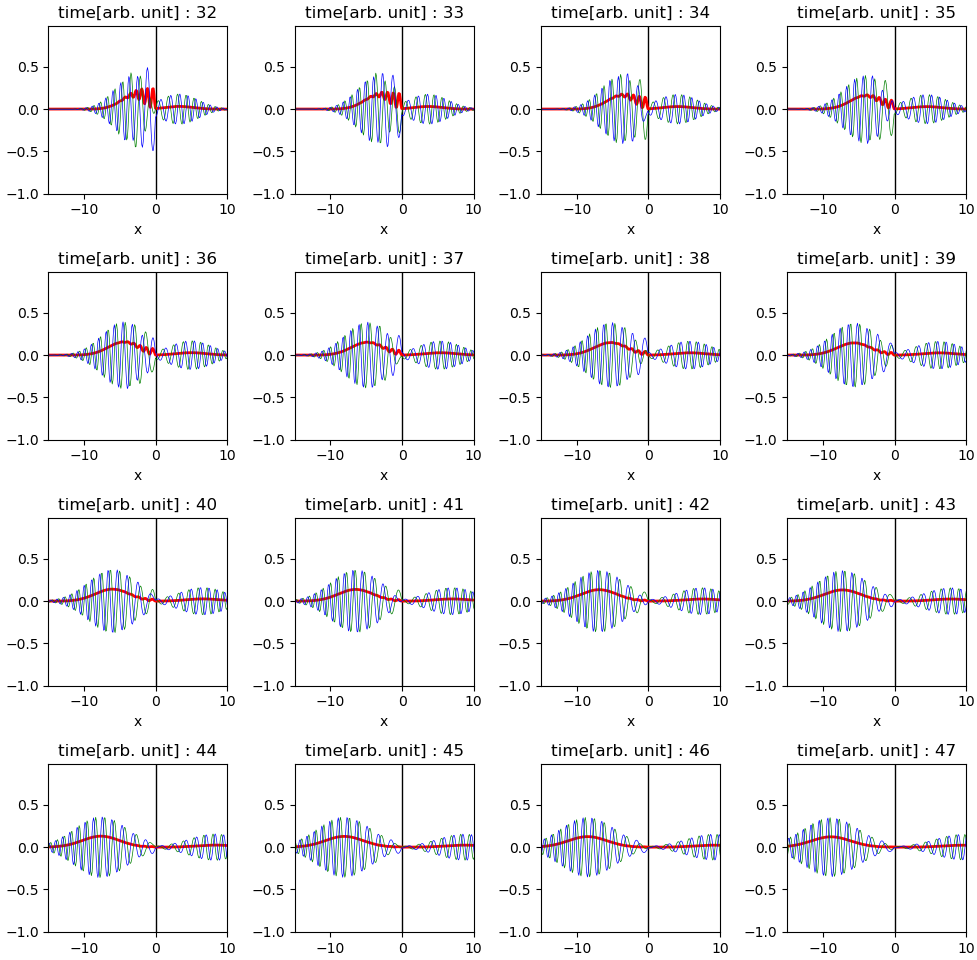
시간이 좀 더 지나게 되면 반사파와 투과파가 완전히 분리 됩니다. 반사파와 투과파는 모두 파동 묶음의 형태를 갖게 됩니다. 투과율과 반사율을 구하고 싶다면 $x \lt 0, x \gt 0$ 영역의 확률 밀도 함수를 적분하면 됩니다.위 문제에서는 매우 단순한 형태의 포텐셜 장벽을 사용하였는데, 다양한 형태의 포텐셜 장벽에 대한 반사와 투과의 정도를 계산 해 보는 것도 매우 흥미로울 것 입니다. 양자역학 수업시간에 공명 터널링(resonance tunnelling)이라는 것을 배웠을 텐데, 시간이 있다면 공명 터널링을 얻을 수 있도록 포텐셜 장벽을 설계하고 시뮬레이션 해 보도록 하겠습니다.
1차원 스케터링 문제는 양자역학을 처음 배울 때 부터 무지하게 많이 풀어 봤겠지만, 실제로 파동 묶음이 포텐셜 장벽을 만나서 반사와 투과를 하는 현상을 기술하는 파동함수 $\psi(x,t)$를 직접 구해보거나, 위와 같이 시각화를 해 본 경험은 많지 않을 것 입니다. 사실, 제가 학부 3학년때 양자역학을 처음 배울 때는 계산해 보지 않았습니다.
이번 포스팅에서는 학부 양자역학에서 가장 처음 다루게 되는 두 문제, 무한 우물에서의 입자와 1차원 스케터링, 에 대해 시간에 의존하는 슈뢰딩거 방정식을 풀어보았습니다. 특정한 형태를 갖는 초기 파동함수 $\psi(x,0)$가 시간의 흐름에 따라서 어떠한 형태로 바뀌는지 $\psi(x,t)$를 수치적인 방법을 통해 구하고 이를 애니메이션으로 나타냈습니다. 보통 수업시간이나 문제를 풀때는 시간에 무관한 슈뢰딩거 방정식을 주로 풀기 때문에 실제로 $\psi(x,t)$가 어떻게 변화하는지를 볼 기회는 많지 않았을 것 입니다. 실제로 $\psi(x,t)$를 구해 보면서 양자역학에 대한 감을 좀 더 잡을 수 있을 것 같습니다. 다음 포스팅에서는 좀 더 다양한 형태의 포텐셜과 초기 조건에 대해 시간에 의존하는 슈뢰딩거 방정식을 풀어 보도록 하겠습니다.
'물리학' 카테고리의 다른 글
| 여과percolation 이론을 컴퓨터를 이용하여 접근하기 (0) | 2023.05.11 |
|---|---|
| 시간에 따른 파동 함수의 변화 계산 하기 102 : 단조화 진동자와 결맞은 상태(coherent state) (0) | 2022.06.04 |
| 렌즈, 물방울에 의한 빛의 굴절 : 공간에 따라 굴절률이 변하는 상황에서 Eikonal 방정식 풀기 + 신기루 현상 설명 (0) | 2022.04.17 |
| 빛의 진행 경로와 페르마의 원리와 Eikonal(아이코널) 방정식 : 페르마의 원리로 부터 스넬의 법칙 유도와 수치해법으로 문제 풀기(파이썬 코드) (1) | 2022.04.16 |
| 중심력장 하에서 입자의 운동 (1) : 수치 미분 방정식 해법을 이용하여 문제 풀기 + 파이썬 시뮬레이션 코드 (0) | 2022.04.09 |



