여과 이론이 무엇인지 알아보기 전에 어쩌면(?) 일상생활에서도 겪을 수 있는 일화를 예시로 들어 보도록 하겠습니다.

위 그림은 체스판과 같은 격자를 나태낸 것 입니다. 격자의 작은 사각형에 흰색 혹은 검은색으로 색칠을 하였습니다. 기본 색깔이 흰색이라고 한다면, 일부분에 검은색을 칠했다고 할 수 있습니다. 이 격자의 아랫쪽에 시작이라고 쓰여진 곳에서 시작하여 도착이라고 쓰여진 반대편 쪽으로 가려고 합니다. 단, 격자에서 검은색 부분을 통해서만 이동할 수 있고, 각 위치를 기준으로 상-하-좌-우로만 움직일 수 있다고 하겠습니다. 시작점에서 부터 도착점까지 갈 수 있을까요?

답은 쉽습니다. 위 그림에서 붉은색으로 칠한 길을 따라가면 됩니다. 위 그림에서 조각(가장 작은 사각형)은 64개이며, 이 중에서 검은색으로 칠한 조각의 갯수는 28개 입니다.

똑같이 28개의 조각에 검은색을 칠한 배치입니다. 이 배치에서는 시작점에서 부터 도착점까지 검은색 조각만을 통해서는 도달할 수 없습니다. 동일한 숫자의 검은색 조각을 배치하였으나, 이 검은색 조각을 어떻게 배치하느냐에 따라서 시작점에서 도착점까지 갈 수 있을 수도 있고, 반대로 그렇지 못 할 수 도 있습니다.
시작점에서 도착점까지 갈 수 있기 위해 필요한 최소한의 검은색 조각은 8개 입니다.

위 그림처럼 검은색 조각을 한 줄로 배치하면, 단 8개의 조각만으로 시작점에서 도착점까지 도달할 수 있습니다. 물론 8개의 조각으로 반대편으로 가기 위해서는 위 그림과 같이 모든 조각을 도착점을 향해 한 줄로 배치해야 합니다. 그렇지 않은 경우에는 도착점으로 도달할 수 없습니다.
이 문제를 약간 더 분석해 보겠습니다. 64개의 조각에 8개의 검은색을 배치할 수 있는 방법의 갯수는
$${}_{64}C_8 = 4,426,165,368$$
개 입니다. 실로 큰 숫자 입니다. 이 갯수 만큼의 조각 배치의 경우의 수 중에서 단 8개의 배치가 시작점에서 도착점까지 연결할 수 있는 배치 입니다. 그 비율은
$$P = \frac{8}{4,426,165,368} = 1.8 \times 10^{-9}$$
입니다. 검은 조각의 갯수가 많으면 당연히 시작에서 도착점까지 연결할 수 있는 배치의 경우의 수는 더 늘어납니다.
여과 이론이란?
여과 이론percolation theory는 위에서 설명한 일상 생활(?)의 예시를 수학적, 물리학적으로 정교하게 연구하는 분야입니다. 위 예시에서는 흰색 바탕에 검은색 조각을 샐칙 하는 것으로 예시를 들었지만, 보다 더 물리학적으로 의미 있는 예시는 도체와 부도체의 배치에 따라 시작 지점에서 도착 지점까지 전기가 흐르게 하는 도체 연결 경로가 존재하는지 혹은 그렇지 않은지를 조사하는 것 입니다. 위 예시에 대응을 시키면, 흰색 조각은 부도체, 검은색 조각은 도체로 하여 생각할 수 있습니다. 도체 연결 망이 시작 지점 부터 도착 지점까지 연결 돼 있으면, 이 시스템에는 전기가 흐르게 되고, 그렇지 않으면 전기가 흐르지 않게 됩니다.
여과는 percolation을 우리말로 옮긴 것으로 한자로 濾過로 쓰여집니다. 그런데 여과를 사전에서 찾아 보면 제일 처음 나오는 영어 단어는 filtration 입니다. 사실 일상적인 용어에서의 여과는 여과 이론에서 말하는 여과와는 정확히 같은 것은 아닌 것 같습니다. 어쨌든 여과라는 것은 한 쪽에서 흐르기 시작한 액체(혹은 일반적으로 입자)가 필터 혹은 일반적으로 흐름을 방해하는 물질을 거쳐 계속 흐르는 것을 의미 합니다. 이 일상 생활에서의 여과의 의미가 여과 이론의 여과와 완전히 같은 것은 아닌것 같지만, 일맥상통하는 의미 인것 같기도합니다. 바로 위 문단에서 물리적으로 의미 있는 여과 이론의 대상이 도체 / 부도체로 이루어진 물질 시스템으로 생각하였는데, 만일 이를 물(액체 혹은 일반적으로 입자)이 흐를 수 있는 부분 / 물리 흐르지 못 하는 부분으로 이루어진 어떠한 물체라고 생각했을 때, 한 쪽 (시작 지점)에서 흐르기 시작한 물이 다른 쪽 (도착 지점)까지 흘러갈 수 있는지 아닌지로 생각할 수도 있습니다.
(아래에서 부터는 논의의 편의를 위해서 맨 위에서 설명했던 일상생활의 예시를 사용하도록 하겠습니다. 즉, 전체 시스템이 흰색 조각으로 돼 있을 때, 이 중 일부분에 특정 갯수의 검은색 조각을 배치한 것을 고려하도록 하겠습니다. 물리적인 상황에 맞게 검은색 조각은 도체 혹은 물이 흐를 수 있는 물질을 의미 합니다)
여과 이론에서 핵심이 되는 개념은 말 그대로 여과 입니다. 굳이 따로 설명이 필요한가 싶지만, 여과는 시작 지점에서 부터 도착 지점까지 검은색 조각만으로 이루어진 경로가 있다는 것을 의미 합니다. 또한 전체 조각에서 검은색 조각의 갯수의 비율이 $p$라고 할 때, 시스템이 여과가 될 확률 $P$을 구하는 것은 매우 중요한 문제입니다. (여기서 소문자 $p$와 대문제 $P$가 사용되는데 혼동하지 않도록 주의해 주시기 바랍니다) 우리는 이미 위에서 $8 \times 8$ 격자로 이루어진 시스템에서 $p = \frac{8}{64} = \frac{1}{8} = 0.125$ 일때, $P = 1.8 \times 10^{-9}$ 라는 것을 이미 계산해 보았습니다.
컴퓨터로 계산하는 여과 이론
일반적으로 주어진 $N \times N$ 격자에서 $p$에 따른 $P$를 계산하는 것은 매우 어렵습니다. 위에서 $N = 8, p = \frac{1}{8}$ 인 문제에서는 여과를 일으키는 검은색 조각의 배치는 모든 검은색 조각이 일렬로 배치된 단 한 경우 밖에 없습니다. 따라서, 여과를 일으키는 검은색 조각의 배치의 경우의 수를 찾는 것이 매우 쉬웠습니다. 그러나, 예를들어 검은색 조각의 갯수가 30개 일때, 여과를 일으키는 검은색 조각의 배치의 경우의 수를 찾는 것은 일반적으로 매우 어렵습니다. 게다가 지금까지는 매우 간단한 격자 (정사각형 형태의 격자)를 생각했지만, 격자의 형태가 매우 이상한 모양을 갖는다면, 해석적인 방법으로 계산하기란 불가능 합니다. 물론, 당연히 해석적으로 계산이 가능한 부분도 있고, 해석적으로 계산을 하기 위해서 많은 수학자와 물리학자들이 계속해서 여과 이론을 연구 하고 있습니다.
따라서, 이번 포스팅에서는 컴퓨터를 이용하여 $p$에 따른 $P$를 계산해 보도록 하겠습니다.
$N = 10, p = 0.5$ 인 경우에서 구체적인 예시

지금까지 앞에서는 흰색 / 검은색으로 표시하였는데, 지금 부터는 편의상 붉은색 / 노란색으로 표시하도록 하겠습니다. 특별한 이유는 없고, 파이썬 프로그래밍을 하고 그래프를 그리는 과정에서 붉은색 / 노란색 / 녹색으로 표시하는 것이 조금 더 편하고 이쁘기 때문입니다. 전체 격자의 조각 100개 중에서 50개는 붉은색, 50개는 노란색 입니다. 이와 같은 배치에서 시작 지점 (아래쪽)에서 도착 지점 (위쪽)으로 여과 하는 경로가 있을까요? 답은 없다 입니다. 도착 지점에서 부터 연결된 노란색 조각을 모두 연결하면,

위 그래프와 같이 녹색 조각들이 얻어집니다. 녹색 조각은 도착 지점까지 연결 돼 있지 않습니다. 따라서, 위와 같이 구체적인 배치에서는 여과가 일어나지 않았습니다.
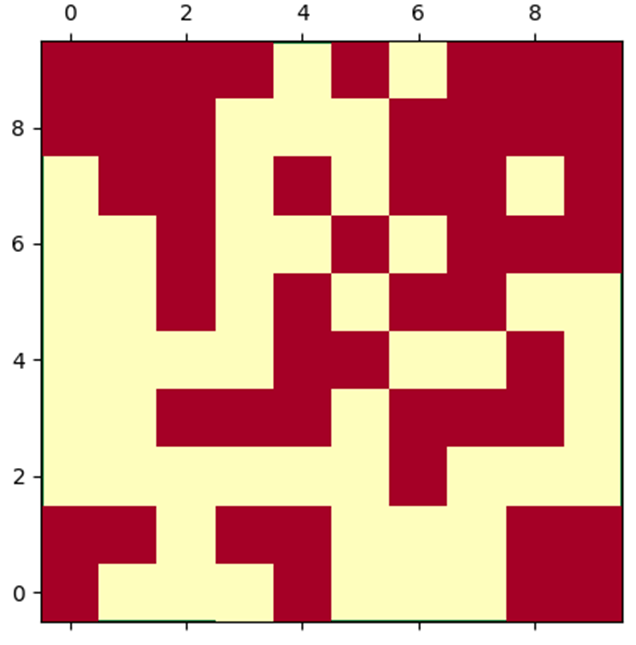
동일한 조건 ($N = 10, p = 0.5$) 에서 다른 형태의 배치를 생각해 보겠습니다. 위 배치에서 맨 아랫줄에 있는 노란색 격자와 연결 돼 있는 모든 노란색 격자를 녹색으로 칠해 보면,
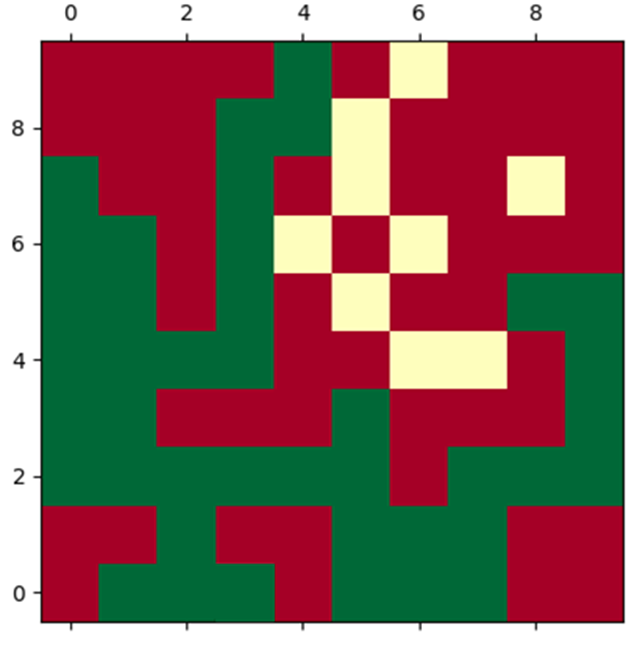
위와 같습니다. 이와 같은 배치에서는 여과가 이루어 졌습니다.
동일한 조건 ($N = 10, p = 0.5$)에서 모든 배치의 경우의 수에 대해서 여과 혹은 여과가 되지 않음을 확인하면 좋겠지만, 이 조건에서 붉은색 / 노란색 조각을 배치할 수 있는 모든 경우의 수는
$${}_{100}C_{50} = 1.01 \times 10^{29}$$
개나 됩니다. 전 세계의 슈퍼컴퓨터를 다 동원하더라도 이 숫자 만큼의 경우의 수는 모두 계산 할 수 없습니다.
따라서, 전체 경우의 수에 대해서 계산을 하는 것은 불가능 하고, 이 중에서 선택된 몇 몇개의 경우에 대해서만 계산을 할 수 밖에 없습니다. 우리의 컴퓨터의 계산 능력이 허락되는 한에서 많은 경우를 조사할 수 밖에 없습니다.
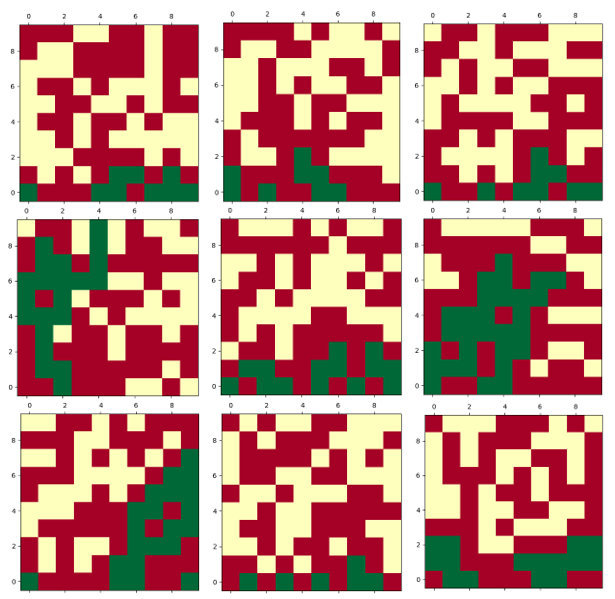
위 그림은 $N = 10, p = 0.5$ 의 조건에서 서로 다른 9개의 경우의 수에 대한 계산을 한 것 입니다. 위 9개의 배치 경우의 수 중에서 한 개의 배치에서 여과가 이루어졌습니다. 위 예시로만 한정 한다면 $P = \frac{1}{9} = 0.111$ 입니다. 배치의 경우의 수를 더 크게 한다면, 이에 따른 $P$ 값은
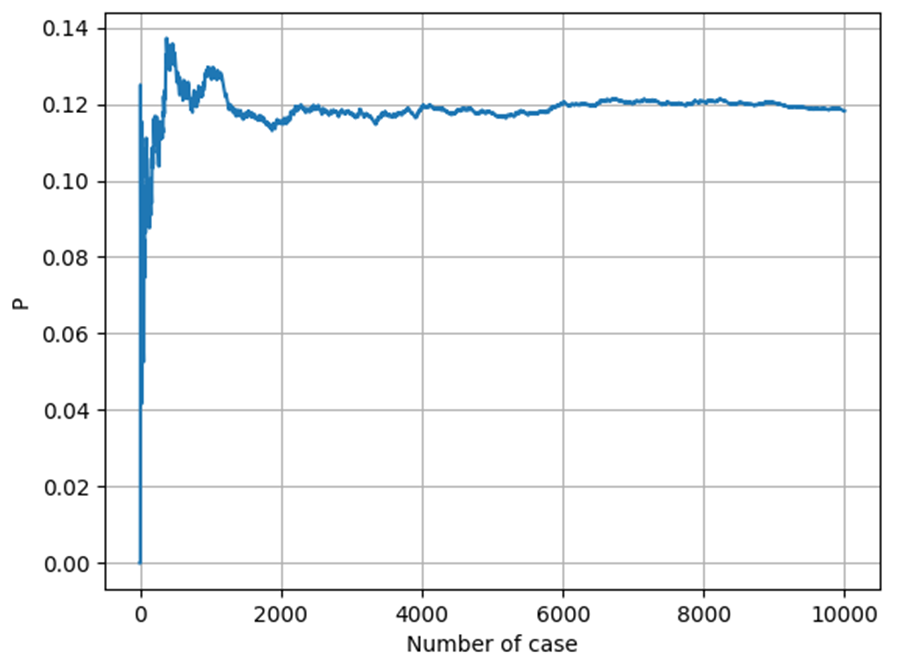
위와 같습니다. X축을 로그 스케일로 그리면,
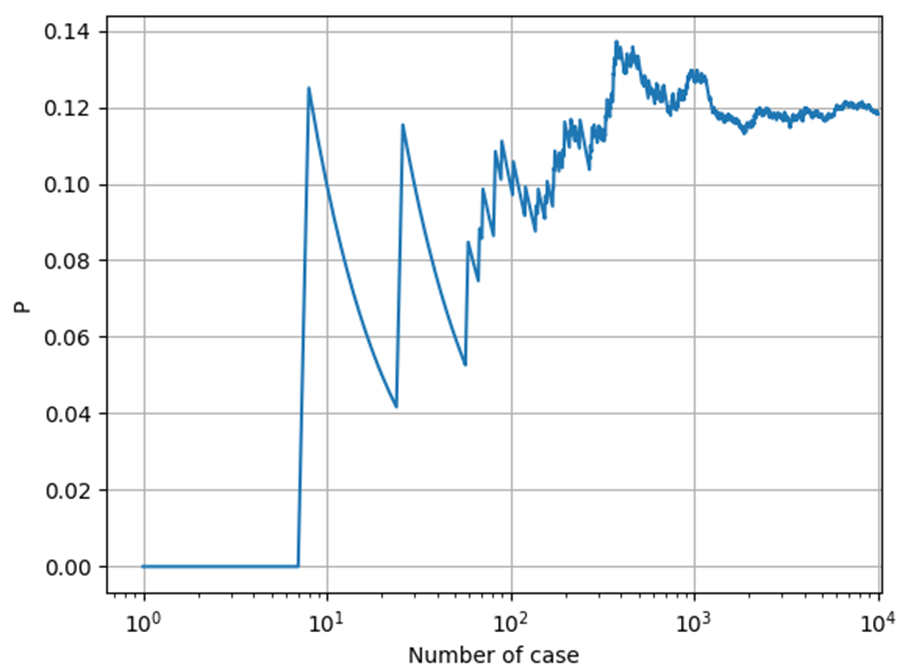
위와 같습니다. 경우의 숫자를 작게 한다면, $P$ 값이 커졌다 작아졌다 하지만, 경우의 숫자가 4,000회가 넘어가면 약 0.12 값에 수렴합니다. 물론, 정확하게 모든 경우의 수를 계산한 것은 아니지만, 이 결과를 통해 유추한다면 모든 경우의 수에 대해서 계산을 하면 대략 0.12를 얻을 것 입니다. 요약하면, $N = 10, p = 0.5$ 인 경우, $P = 0.12$ 입니다.
일반적인 $p$ 에 대한 $P$ 구하기
위에서는 $p = 0.5$에 대해서 차근히 계산을 해 보았습니다. 이제 $[0, 1]$ 사이에 있는 다른 $p$값에 대해서 $P$를 계산해 보도록 하겠습니다. $[0, 1]$ 사이의 모든 값에 대해서 계산을 할 수는 없기 때문에, 적당한 간격을 갖고 계산을 해 보도록 하겠습니다. 물론 계산의 편의상 $N = 10$으로 두었습니다.
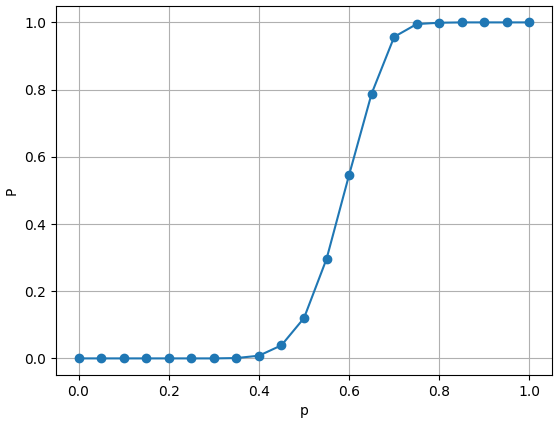
위 그래프는 $[0, 1]$ 영역에서 0.05 간격에 따른 $p$에 대해서 이에 대응되는 $P$를 계산한 그래프 입니다.
약간 신기(?) 한 것은 $p$가 작을 때($p \lt 0.4$)는 $p$가 증가하더라도 $P$가 (거의) 증가하지 않다는 것 입니다. 그러나 대략 $p = 0.6$에서는 $p$의 증가에 따라 $P$가 매우 크게 증가합니다. 그리고 다시 $p$가 커지면($p \gt 0.8$) $P = 1$이 됩니다. 처음 생각했을 때는 $p$가 증가함에 따라 $P$ 역시 서서히 증가하여 0에서 1이 될 것이라 생각했는데, 실제 계산 결과는 이와는 좀 다른 양상입니다.
조금 큰 $N$에 대해서 같은 계산 다시 해 보기
지금까지는 $N = 10$에 대해서 계산을 하였는데, 이번에는 $N = 70$에 대해서 같은 계산을 반복해 보도록 하겠습니다. 결과($p$ vs $P$ 그래프)의 양상이 어떻게 변화할지 예측해 보는 것도 재미있을 것 같습니다.
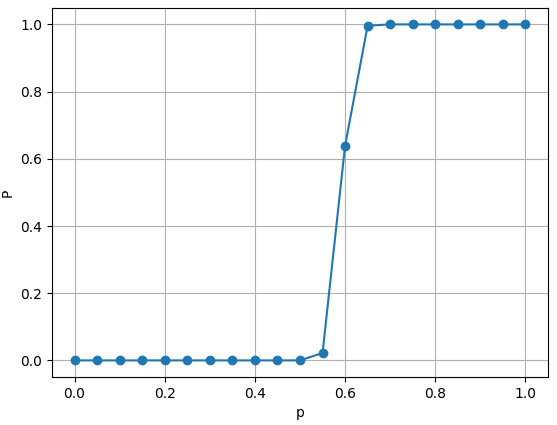
결과는 위와 같습니다. $N = 10$의 결과에서는 $P$ 값이 0에서 부터 1까지 어느 정도는 서서히 증가하였는데, $N = 70$의 결과에서는 $P$값이 0부터 1까지 $p = 0.6$ 근처에서 급격하게 증가합니다. $p = 0.5$에서는 $P = 0$이었는데, $p = 0.65$에서는 $P = 1$가 됩니다! 격자의 사이즈를 더 키운다면, $p$ vs $P$ 그래프가 특정값($p = 0.6$) 근방에서 더욱 더 가파르게 증가할 것이라고 예상할 수 있습니다. 이 결과를 통해서 $N$이 훨씬 더 큰 값이 된다면 $P$값이 $p = 0.6$ 근처에서 0에서 1로 불연속적으로 증가할 것으로 예상할 수 있습니다.
$p = 0.592$ 보다 크고 작음에 따라 완전히 달라지는 여과
단란의 제목에서 이미 결과를 언급했는데, $p$의 값이 $0.529$ 보다 크냐 작느냐에 따라서 여과의 여부가 완전히 달라집니다. $N = 200$ 인 경우에 대해서 $p = 0.59$인 경우, 구체적인 예시는 아래와 같습니다.
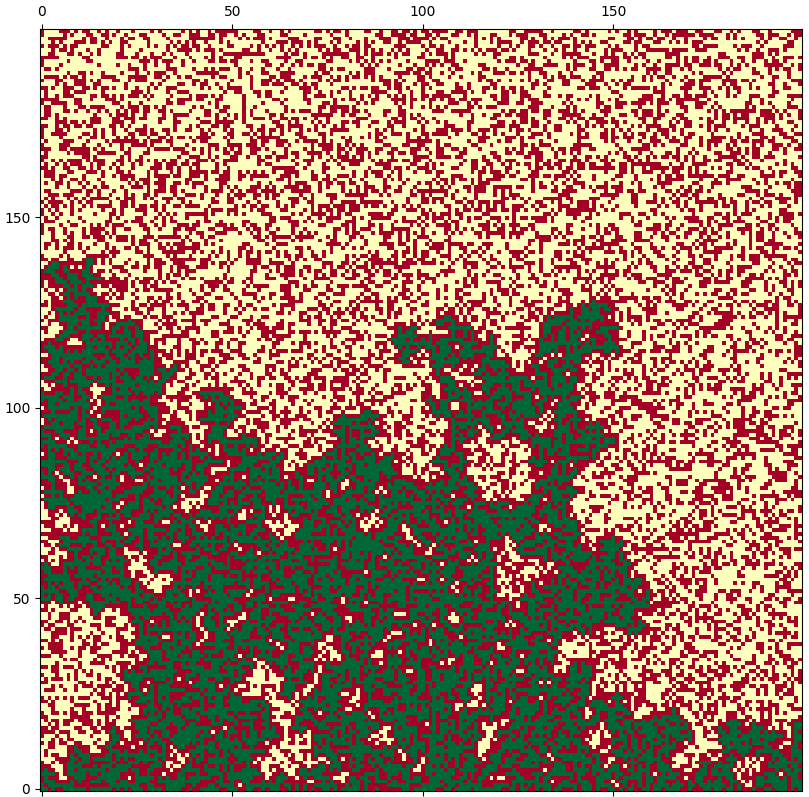
이 시뮬레이션에는 무작위성이 들어가 있기 때문에, 항상 이와 같은 결과를 얻는 것은 아니지만 대체적으로 이와 비슷한 결과를 얻게 됩니다.
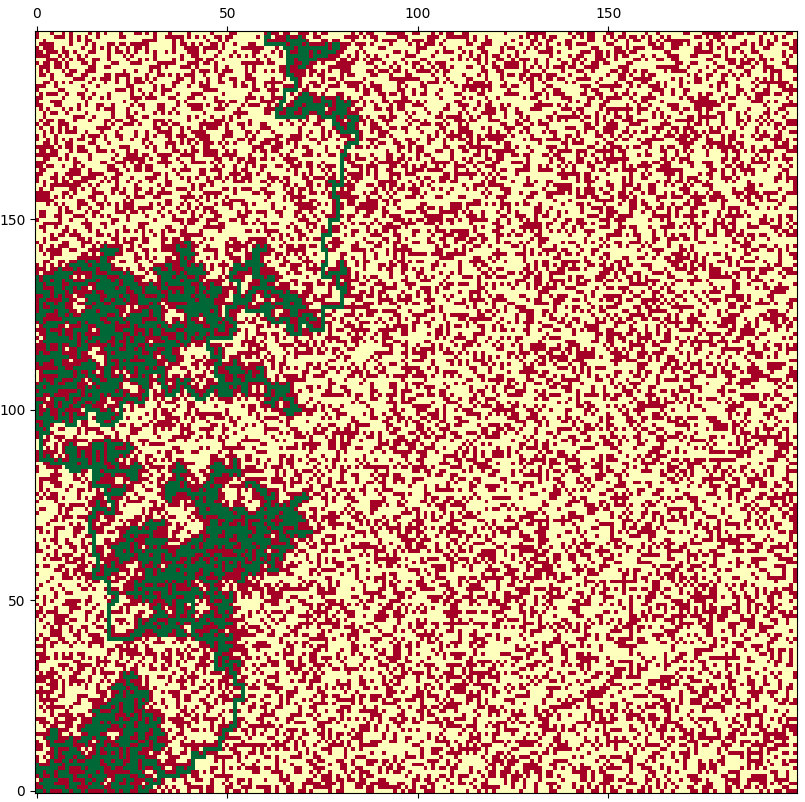
$p = 0.6$ 의 경우, 구체적인 예시는 위와 같습니다. $p$가 $0.01$만큼만 증가하였는데, 시작 지점에서 부터 도착 지점까지 도달할 수 있는 여과 경로가 생겼습니다. (여러개의 서로 다른 여과 경로가 있을 수 있겠지만, 프로그램 실행에서 찾아진 하나의 경로를 그린 것 입니다)
$N$이 매우 커질 경우, 이와 같이 특정한 값 $p_c$를 기준으로 $p \gt p_c$인 경우 여과 경로가 생기고, $p \lt p_c$인 경우에는 여과 경로가 생기지 않습니다. 여기서 $p_c$ 값은 대략 $0.592$이고 이 값을 전이 한계점transition thresold 라고 합니다.
$N$의 값에 따라 양상이 달라지는 이유
위에서 $p$ vs $P$ 그래프는 $N$의 값이 커질 수록 급격하게 변화합니다. $N$이 작은 경우에는 $p \lt p_c$ 인 경우에도 여과 경로가 생기기도 하고($P \gt 0$), 반대로 $p \gt p_c$ 인데도 여과 경로가 생기기 않기도($P \lt 0$) 합니다. 이는 $N$이 작을 때는 전체 경우의 수가 작고, 이 작은 경우의 수 중에서 매우 이상하게 생긴 여과 경로가 차지하는 비율이 0이 아니기 때문입니다. 그러나 $N$이 커지게 된다면, 극단적으로 운이 좋아서 $p$가 작아도 여과 경로가 생기는 경우(예를들면 모든 여과 격자가 한 줄로 배치되는 경우)의 비율은 0으로 수렴하게 됩니다. 일상의 용어로 요약하자면 $N$이 커지면 "운빨"로 전이 경로가 생성되는 경우가 없다 라고 할 수 있습니다.
여과 전이percolation transition
($N$이 큰 경우에, 정확히는 $N \rightarrow \infty$ 인 경우에) $p$값이 $p_c$ 보다 작은 값에서는 ($p$값에 상관 없이) $P=0$이었다가, $p$값이 $p_c$ 보다 커지는 순간에 ($p$값에 상관 없이) $P=1$로 갑자기 커지는 현상은 마치 물이 섭시 99도에서는 그냥 뜨거운 물이다가 100도가 되면 끓어서 수증기가 되는 것과 닮아 있습니다. 일반적으로 이와 같이 물리량의 작은 변화에 따라 다른 물리량이 급격하게 달라지는 현상을 전이transition이라고 합니다. 온도의 변화에 따라 물의 상태(고체, 액체, 기체)이 급격하게 달라지는 현상 혹은 온도의 변화에 따라 물체의 자기적인 성질(강자성, 반자성)이 급격하게 달라지는 현상이 전이의 대표적인 예시 입니다.
여과 현상 역시 위에서 시뮬레이션을 통해서 살펴본 것 처럼, $p$값의 아주 작은 변화에 따라서 $P$값이 급격하게 변하는 전이 현상 중에 하나 입니다. 앞에서 실제 물리현상을 예로 들었던 물이나 자기 현상의 전이의 경우 상phase가 변하는 상전이phase transition이라면, 여과 현상에서는 기하학적 특성(연결된 격자의 모양이나 크기)이 크게 바뀌는 기하학적인 전이geometric transition입니다.
여과 전이 한계값percolation threshold
여과 전이의 양상이나 $p_c$ 값은 격자의 성질에 따라서 달라집니다. 우리가 지금까지 살펴본 2차원 정사각형 격자의 경우 수치적인 계산을 통해서 $p_c = 0.59274...$ 라는 것이 알려져 있습니다. 불행히도(?) 해석적인 방법으로는 $p_c$값을 구할 수 없기에, 다양한 방법으로 $p_c$값을 어림하고 있습니다. 특정한 형태의 격자에서는 $p_c$ 값을 해석적인 방식으로 계산할 수 도 있는데, (개인적으로는 예상 밖에도) 복잡한 격자에서 해석적인 값을 얻어 낼 수 있다는 것이 다소 신기하기도 합니다. 다양한 격자의 형태에 따른 $p_c$ 값은 위키피디아 페이지를 통해 확인할 수 있습니다. https://en.wikipedia.org/wiki/Percolation_threshold
Percolation threshold - Wikipedia
en.wikipedia.org
일반적인 여과 전이
시각적인 편의를 위해서 지금까지는 2차원 공간에서의 격자를 생각했지만, 일반적으로는 3차원, 4차원 혹은 임의의 차원에 놓인 격자 공간에서 여과 전이를 생각할 수 있습니다. 격자 뿐 아니라 일반적인 그래프에서 여과 전이를 고려할 수 도 있습니다. 격자가 놓인 공간 차원의 증가에 따라 여과 전이가 어떻게 달라지는지에 대해서는 매우 재미난 논의가 가능하지만, 이는 어렵고 방대한 내용이라서 이번 포스팅에서 다룰 만한 내용은 아닌것 같아서 생략합니다. 시간이 허락된다면 다음 포스팅에서 하나 하나 다루도록 하겠습니다. 어쩌면, 이 포스팅에서 다룬 내용보다는 다음 포스팅에서 다룰 내용이 더 중요하다고 볼 수 있습니다.
일반적인 전이 이론과의 접목
앞에서 이미 설명한 것과 같이 여과 전이는 일반적인 전이 이론의 하나 입니다. 따라서, 일반적인 전이 이론에서 활용 될 수 있는 방법론을 활용하여 여과 전이를 설명할 수 있습니다. 예를들면 전이 한계값 $p_c$ 근처에서 $P$값의 정성적인 변화의 양상이라든가 공간 차원의 증가에 따른 여과 정도의 양상 등이 있습니다. 이 부분 역시 매우 재미난 논의가 가능하지만 이번 포스팅에서 다룰만한 내용은 아니라고 생각합니다
파이썬 코드
위 계산에서 활용한 파이썬 코드를 공유 합니다. $N \times N$ 격자 공간에서 $p$ 비율 만큼의 격자가 검은색 격자(여과 격자) 일 때, 격자를 배치하고 여과 가능성 여부를 계산하는 프로그램 입니다. 당연히 최적화가 잘 된 코드는 아니며 빠르게 코딩을 할 수 있도록 "대충" 코딩한 프로그램입니다. 주어진 검은색 격자의 그래프에서 DSF 알고리듬을 활용하여 여과 경로를 찾습니다.
import numpy as np
from matplotlib import pyplot as plt
import sys
import random
sys.setrecursionlimit(10 ** 6)
move = [[1, 0], [0, 1], [0, -1], [-1, 0]]
def select_position(N, Nreturn):
p = []
for x in range(N):
for y in range(N):
p.append([x, y])
random.shuffle(p)
return p[:Nreturn]
class DFS():
def __init__(self, A, N):
self.A = A
self.Visited = []
self.move = [[1, 0], [0, 1], [0, -1], [-1, 0]]
self.N = N
self.find = False
def return_start(self):
self.start = [[0, y] for y in range(self.N) if self.A[0, y] == 1]
def return_populated(self):
self.populated = []
for x in range(self.N):
for y in range(self.N):
if self.A[x, y] == 1:
self.populated.append([x, y])
def run_connect(self):
self.return_start()
while len(self.start) > 0 and (not self.find):
xs, ys = self.start[0]
self.start.remove([xs, ys])
self.check_connectivity(xs, ys)
return self.find
def check_connectivity(self, x, y):
if not self.find:
self.Visited.append([x, y])
if self.N - 1 == x:
self.find = True
if x == 0 and [x, y] in self.start:
self.start.remove([x, y])
for dx, dy in self.move:
nx, ny = x + dx, y + dy
if (not [nx, ny] in self.Visited) and (0 <= nx <= self.N - 1 and 0 <= ny <= self.N - 1) and (
self.A[nx, ny] == 1):
self.check_connectivity(nx, ny)
def get_percolation_probability(N, concentration):
A = np.zeros([N, N])
Nc = int(N * N * concentration)
position = select_position(N, Nc)
for x, y in position:
A[x, y] = 1
dsf = DFS(A, N)
dsf.run_connect()
for x, y in dsf.Visited:
dsf.A[x, y] = 2
plt.matshow(dsf.A, origin='lower', cmap=plt.get_cmap("RdYlGn"))
plt.show()
plt.close('all')
if __name__ == '__main__':
N = 100
p = 0.55
get_percolation_probability(N, p)
'물리학' 카테고리의 다른 글
| 중심력장 하에서 입자의 운동 (2) : 태양계 행성의 운동 시뮬레이션 + 파이썬 코드 (1) | 2023.05.17 |
|---|---|
| 시간에 따른 파동 함수의 변화 계산 하기 102 : 단조화 진동자와 결맞은 상태(coherent state) (0) | 2022.06.04 |
| 시간에 따른 파동 함수의 변화 계산 하기 101 : 상자 속 입자 문제와 1차원 스케터링 문제 (0) | 2022.06.01 |
| 렌즈, 물방울에 의한 빛의 굴절 : 공간에 따라 굴절률이 변하는 상황에서 Eikonal 방정식 풀기 + 신기루 현상 설명 (0) | 2022.04.17 |
| 빛의 진행 경로와 페르마의 원리와 Eikonal(아이코널) 방정식 : 페르마의 원리로 부터 스넬의 법칙 유도와 수치해법으로 문제 풀기(파이썬 코드) (1) | 2022.04.16 |



