페르마의 원리
위치에 따라 굴절률이 바뀌는 물질 속에서 빛의 진행 경로에 대해서 다룬 지난 두 번의 포스팅에서 빛의 진행 경로는 "두 점을 잇는 최단 시간 곡선" 이라는 페르마이 원리로 부터 스넬의 굴절 법칙, 그리고 보다 일반적인 굴절법칙이라고 할 수 있는 Eikonal 방정식에 대해서 알아 보았습니다. 페르마의 원리는 일반적인 변분법 문제로 표현이 되는데,
$$0 = \delta T = \delta \int_{\vec{x}_A}^{\vec{x}_B} n(\vec{x}) ds$$
입니다. 여기서 $n(\vec{x})ds$를 흔히 광경로 길이(optical path length) 라고 합니다. $ds$면 단순히 길이(length)인데, 굴절률이 곱해졌기 때문에 광경로 길이 라고 합니다. 이 포스팅에서는 광경로 길이의 미소 길이를 $dl$로 표현하겠습니다. 이 경우 $dl = n(\vec{x})ds$가 되고, $dl$을 적당히 적분한 값을 $L$이라 하겠습니다. 그러면, 위 변분법 문제는 $ = \delta L$ 으로 쓸 수 있습니다.
광경로
공간상의 두 점 $\vec{x}_A, \vec{x}_B$을 잇는 선분을 생각할 때, 두 점 사이의 거리 $d_{AB} = |\vec{x}_A - \vec{x}_B|$는 일정하더라도, 선분 상에 존재하는 점에서 굴절률 $n(\vec{x})$가 시시 때때로 변한다고 한다면 각 시점에서의 광경로 길이 $L_{AB} = \int_{\vec{x}_A}^{\vec{x}_B} n(\vec{x})ds$ 역시 시시 때때로 변하게 됩니다. 또 다르게 생각한다면, $\vec{x}_A, \vec{x}_B$ 사이의 거리와 $\vec{x}_C \vec{x}_D$ 사이의 거리는 같다고 하더라도, 즉 $|\vec{x}_A - \vec{x}_B| = |\vec{x}_C - \vec{x}_D|$ 이더라도, 점 $\vec{x}_A, \vec{x}_B$가 있는 공간의 굴절률과 점 $\vec{x}_C, \vec{x}_D$가 있는 공간의 굴절률이 서로 다르다면 $\vec{x}_A, \vec{x}_B$ 사이의 광경로 길이 $L_{AB}$ 와 $\vec{x}_C, \vec{x}_D$ 사이의 광경로 길이 $L_{CD}$는 당연히 다르게 됩니다.
빛의 경로의 수학적 일반화
지금까지는 "빛"에 대해서 다루었고, "빛"의 경로를 찾았습니다. 그러나 이제 부터는 "빛" 이라는 것을 까먹도록 하겠습니다. 그냥 단순히 공간상에 $n(\vec{x}) \ge 1$ 이라는 함수가 정의되어 있고, 두 점 $\vec{x}, \vec{x} + d\vec{x}$ 사이의 거리가 $|d\vec{x}|$ 가 아닌 $n(\vec{x}) |d\vec{x}|$ 로 주어진다고 생각하겠습니다. 즉 길이를 미소 길이 $ds = |d\vec{x}|$로 생각하는 것이 아니라 미소 "광" 경로 길이 $dl = n(\vec{x})ds$로 생각하는 것 입니다. 이는 두 점 사이의 거리를 일반화 한 것으로 $n(x) =1$ 인 경우, 우리가 원래 생각하던 두 점 사이의 거리가 됩니다. $n(\vec{x})$가 공간에 따라서 변화한다면, 이는 공간에 따라서 자의 눈금이 변하는 것이라고 생각할 수 있습니다. $n(\vec{x})$가 큰 곳에서는 자의 눈금의 간격이 짧아졌다고 할 수 있고, $n(\vec{x})$가 작은 곳에서는 자의 눈금이 넓어졌다고 생각할 수 있습니다.
바로 위 문단에서 수학 기호 표현은 "광경로"에 대한 수학 기호 표현을 그대로 물려 받은 것으로, 이제 부터 우리는 "빛"에 대해서는 완전히 까먹을 것이기 때문에 논의의 편의를 위해서 완전히 새로운 수학 기호를 사용하도록 하겠습니다. 앞으로는 $ds$가 위 문단에서 $dl$의 역할을 할 것이며, 기존의 $ds$는 $dx$가 그 역할을 대신할 것 입니다. $ds = n(\vec{x})dx$가 됩니다. 보통 $dx$라고 쓰면 $x$축 방향으로의 미소 변위를 의미 하는데, 우리는 일반적으로 2차원 혹은 3차원 공간을 생각할 것이기 때문에, $dy, dz$에 대해서도 동일하게 쓸 수 있습니다. 따라서, $ds = n(\vec{x})dx$ 라고 쓴 것은 $ds_x = n(\vec{x})dx$ 라고 생각하는 것이 더 명확하며, $ds_y, ds_z$ 도 동일한 방법으로 생각할 수 있습니다. 피타고라스 정리에 따라서 $ds^2 = ds_x^2 + ds_y^2 + ds_z^2$ 가 되고, $ds^2 = n(\vec{x})^2 dx^2 + n(\vec{x})^2 dy^2 + n(\vec{x})^2 dz^2$ 가 됩니다.
이 포스팅, 그리고 이전 포스팅에 걸쳐서 공간상에 굴절률은 스칼라 값으로 생각했습니다. 그러나 실제로 굴절률은 빛의 진행 방향에 따라서 그 값이 달라집니다. 이는 물질의 격자 구조가 등방적(isotropic)하지 않기 때문입니다. 예를들어 물질의 격자 구조가 Tetragonal 이라면, 이 물질 내부에서 빛이 $x$방향으로 진행하는 경우와 $z$방향으로 진행하는 경우의 빛의 속도는 다를 수 있습니다. 왜냐하면, 격자 구조의 $x$방향 격자 상수와 $z$방향 격자 상수가 서로 다르기 때문입니다. 빛의 속도가 방향에 따라 다르기 때문에 $n = \frac{c}{v}$ 로 정의되는 굴절률 역시 방향에 따라 다른값을 가질 수 있고, 따라서 $n(\vec{x})$가 아닌 $n(\vec{x})_x, n(\vec{x})_y, n(\vec{x})_z$ 와 같이 방향을 나타내는 추가적인 인덱스가 필요합니다. 이 성질을 위 문단의 마지막 수식에 적용하면, $ds^2 = n(\vec{x})_x^2 dx^2 + n(\vec{x})_y^2 dy^2 + n(\vec{x})_z^2 dz^2$ 라고 일반화 할 수 있습니다.
위 식을 보다 더 일반화 해 보도록 하겠습니다. 앞 문단에서 "빛"에 대해서 완전히 까먹자고 했는데, 사실 완전히 까먹은 것은 아니고, 조금 더 일반화한 것이었습니다. 이번에야 말로 "빛"에 대해서는 완전히 까먹고, 수학적인 일반화를 해 보도록 하겠습니다. 위 문단의 마지막 $ds^2$에 대한식은 $dx, dy, dz$ 각각에 대한 제곱의 합 입니다. 이를 일반화 하면 $dx, dy, dz$의 이차식을 생각할 수 있습니다. 즉, $dxdy, dydz, dzdx$항을 생각하는 것 입니다. $dxdy, dydz, dzdx$ 서로 다른 방향의 미소 변위의 곲을 기하학적으로 어떻게 생각해야 하는지 (빛의 진행과 어떻게 연관 지어야 하는지) 에 대해서는 우선 생각하지 않도록 하겠습니다. 완전 제곱 형태만을 생각하기 보다는 보다 일반적인 이차형식을 생각하는 것 입니다. 또한, $dx^2, dy^2, dz^2$ 앞에 있는 계수를 $n(\vec{x})_x$와 같은 형태로 썼는데, 이제는 $dxdy, dydz, dzdx$와 같은 항이 있으니, $dx^2 = dxdx$의 의미를 보다 명확하게 하기 위해, $n(\vec{x})_{xx}$로 쓰도록 하겠습니다.
위에서 $dx^2$ 등의 계수를 $n$으로 썼는데, 이는 "굴절률"에서 비롯된 표기법 입니다. "빛"에 대해서는 완전히 잊겠다고 했기 때문에, 이제 부터는 $n$ 대신에 $g$를 이용하여 쓰도록 하겠습니다. 여기까지 설명한 내용을 요약해서 수식으로 쓴다면,
$$\begin{aligned}
ds^2 = & g(\vec{x})_{xx}dxdx + g(\vec{x})_{yy}dydy + g(\vec{x})_{zz}dzdz + g(\vec{x})_{xy}dxdy + g(\vec{x})_{yz}dydz + g(\vec{x})_{zx}dzdx\\
= & \sum_{i, j} g(\vec{x})_{i,j}dx^i dx^j
\end{aligned}$$
가 됩니다. 여기서 $x^1 = x, x^2 = y, x^3 = z$ 입니다. 즉 공간상의 점 $\vec{x}$ 마다 $g(\vec{x})_{i,j} \gt 0$가 정의 돼 있을 때, 점 $\vec{x}$와 점 $\vec{x} + d \vec{x}, d \vec{x} = (dx, dy, dz)$ 사이의 (일반화된) 거리 $ds = \sqrt{\sum_{i, j} g(\vec{x})_{i,j}dx^i dx^j}$ 로 정의 됩니다.
메트릭
지금까지의 이야기는 수학에서 정의하는 메트릭(metric)과 이 메트릭에 의해서 주어지는 길이에 의한 정의를 이전 포스팅에서 다룬 "빛의 경로 문제"에 빗대어 설명한 것 입니다. 위 식에서 $g(\vec{x})_{i,j}$로 쓴 메트릭은 공간상의 "일반화된" 거리를 정의 하는데 사용합니다. 빛의 경로 문제에서 실제로 중요한 것이 두 점 사이의 광경로의 길이였던 것 처럼, 메트릭이 주어진 공간에서 정의된 거리는 메트릭에 의해서 $ds = \sqrt{\sum_{i, j} g(\vec{x})_{i,j}dx^i dx^j}$와 같이 정의 됩니다. 실제 수학에서의 메트릭에 대한 정의와 모티베이션은 이와 다르지만 우리의 물리적 직관을 최대한 활용하여 메트릭을 이해해 본 것 입니다. 메트릭에 대해서 잘 모르는 독자의 이해를 돕기 위해 작성된 글이니 수학적인 엄밀성과는 약간 거리가 있을 수 도 있습니다. (뒷 부분의 내용도 마찬가지 입니다)
구체적인 예시 : 1차원
메트릭과 메트릭에 의해서 정의된 거리(곡선의 길이)에 대해서 "느낄" 수 있는 또 다른 경우를 생각해 보도록 하겠습니다. 이 예시는 굴절률이 위치에 따라 바뀌는 매질 내에서 빛의 경로 문제 보다 더 현실적이면서 직관적인 예시 입니다.
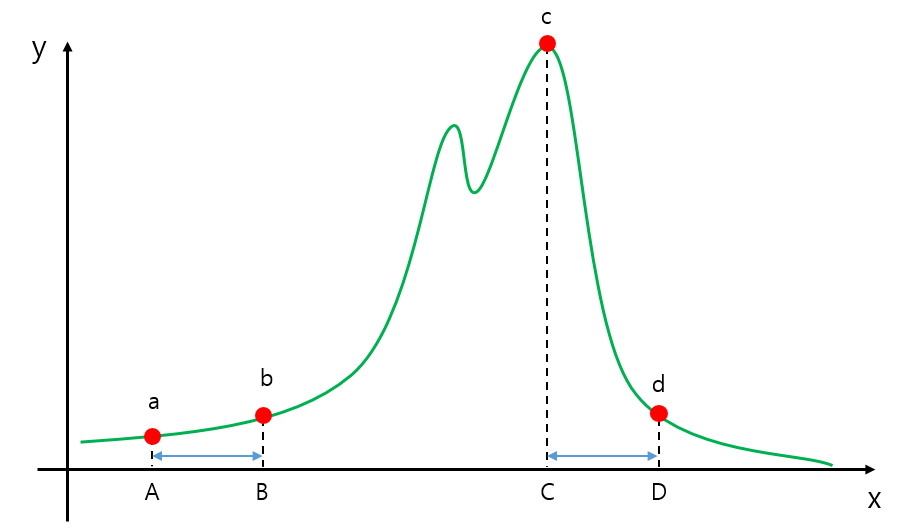
한 등산객이 산을 오르는 것을 생각해 보겠습니다. 산의 모양은 위 그래프의 녹색 선과 같이 생겼습니다. $x$축은 지표면과 나란한 특정한 방향을 하나 선택하여 축을 삼을 것이고, $y$축은 지표면에 수직인 축 입니다. 설명의 편의를 위해서 등산객은 $x-y$ 평면 상에서만 움직인다고 가정하겠습니다. $x$값에 따른 산의 높이 $y$는 함수 $y = f(x)$에 의해 완전히 기술된다고 하겠습니다.
등산객이 $a$지점에서 산을 따라서 (녹색 그래프를 따라서) $b$ 지점으로 이동했다고 할 때, 등산객의 $x$좌표의 변화는 $|B-A|$ 이고, 실제 움직인 거리는 $s = \int_a^b \sqrt{1 + f_x^2}dx$ 가 됩니다. 여기서 $f_x = \frac{df}{dx}$ 입니다. $s$는 단순히 $y = f(x)$로 주어진 곡선의 거리를 구하는 식 입니다. 위 적분식은 미소 변위/거리를 사용하여 $ds = \sqrt{1+ f_x^2} dx$로 표현할 수 도 있습니다. 이는 메트릭이 정의 된 1차원 공간에서의 거리식 $ds = \sqrt{g(x)_{xx}}dx$와 형태가 동일합니다. 즉, 등산객이 산을 따라 "실제 움직인 거리"는 메트릭 $g(x)_{xx} = \sqrt{1 + f_x^2}$로 주어진 공간에서 "$x$ 축 방향으로 움직인 거리"와 동일 합니다. 메트릭 $g(x)_{xx}=1$인 공간에서의 움직임은 단순히 $x$축 상위에서 움직이는 것이라 볼 수 있고, $g(x)_{xx} \ne 1$인 공간에서의 움직임은 산을 따라 ($y = f(x)$그래프를 따라서) 움직이는 것이라 볼 수 있습니다. 메트릭 값이 $1$이 아니기에 실제 움직인 거리 $ds$와 "겉으로 보기에 움직인 거리" $dx$가 다른 것 입니다. 여기서 "겉으로 보기에"는 "하늘에서 내려다 보기에"로 바꿀 수 있습니다. 하늘에서 등산객을 내려다 본다면, 등산객의 $y$방향 움직임을 볼 수 없기 때문에, 등산객이 $x$축 방향으로만 움직인다고 볼 것 입니다.
메트릭 $g(x)_{xx} = \sqrt{1 + f_x^2}$가 위치 $x$에 따라 다르기 때문에, $x$축 방향으로 이동한 거리($dx$)가 같더라도 실제 산을 따라 이동한 거리($ds$)가 위치에 따라 달라지는데, 위 그래프에서 $B-A = D-C$이지만, 점 $a$와 점 $b$ 사이에서 녹색 그래프를 따리 이동한 거리와 점 $c$와 점 $d$ 사이에서 녹색 그래프를 따라 이동한 거리는 서로 다릅니다. $C, D$ 사이의 기울기가 가파르기 때문에 메트릭값이 커진것과 같고, 따라서 실제 이동한 거리는 $c,d$ 사이가 훨씬 더 깁니다.
구체적인 예시 : 2차원
이번에는 차원을 하나 높이고 다른 문제를 생각해 보겠습니다. 실제와 같은 3차원 산 입니다.
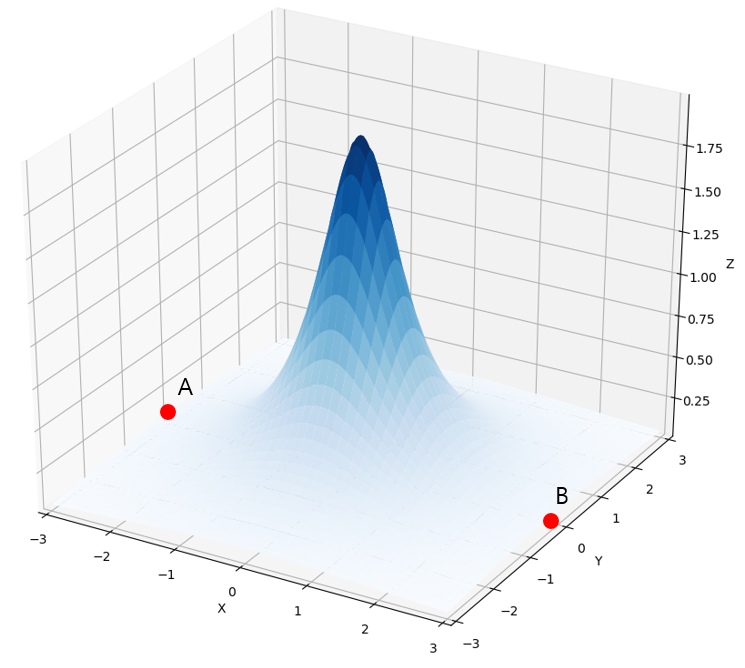
원점에 정상이 있는 위 그래프와 같은 산(지형)을 생각하겠습니다. $(x,y)$에서 산의 높이 $z = f(x,y)$는
$$f(x,y) = \frac{1}{x^2 + y^2 + 0.5}$$
로 모델링 하였습니다. 원점이 정상이고, 원점에서 멀어질수록 급격하게 높이가 낮아지는 산 모양을 만들기 위해 도입된 함수입니다. 분모에 $+0.5$는 원점에서 산의 높이가 하늘을 뚫고 올라기는 것을 방지하기 위해 도입된 값입니다. 원점에서 산의 높이는 $2$가 됩니다.
등산객이 점 $A = (-3,0)$에서 시작하여 점 $B= (3,0)$지점으로 가능 경로를 생각해 보겠습니다. 수 많은 경로가 있지만, 등산객은 "산을 따라 걷는 거리를 최소화 하는 경로"를 원합니다. 이 경우, 등산객은 어떤 경로를 택해야 할까요? 위 "2차원 공간의 산"의 경우를 참고하여 문제를 풀어 보도록 하겠습니다.
등산객은 $x-y$ 평면에서 움직이는 것이 아니라 산을 따라서, 즉 $z = f(x,y)$ 면을 따라서 이동하기 때문에, $x-y$ 평면 사이에서의 거리($dx, dy$)를 최소하 하는 것이 아니라 $ds$ 거리를 구하고 이를 최소화 해야합니다. $ds$를 구하기 위해서는 위 그래프 $z = f(x,y)$에 의해서 주어진 메트릭을 구해야 하는데, $y = f(x)$에서는 $g(x)_{xx} = \sqrt{1 + f_x^2}$로 주어진 것에 착안하면, $z = f(x,y)$인 경우에는 우선 공간 차원이 하나 더 늘었기 때문에, $g(x,y)_{xx}$ 뿐 아니라 $g(x,y)_{yy}, g(x,y)_{xy}$ 도 구해야 합니다. $z = f(x,y)$ 그래프는 3차원 공간의 점 $\vec{S}(x,y) = (x, y, f(x,y))$로 생각할 수 있고, 이 경우,
$$ g(x,y)_{i,j} = \frac{\partial \vec{S}}{\partial x^i} \cdot \frac{\partial \vec{S}}{\partial x^j}$$
로 주어집니다. 이로 부터,
$$ds^2 = (1+f_x^2)dx^2 + (1+f_y^2)dy^2 + (2f_xf_y)dxdy$$
를 얻습니다.
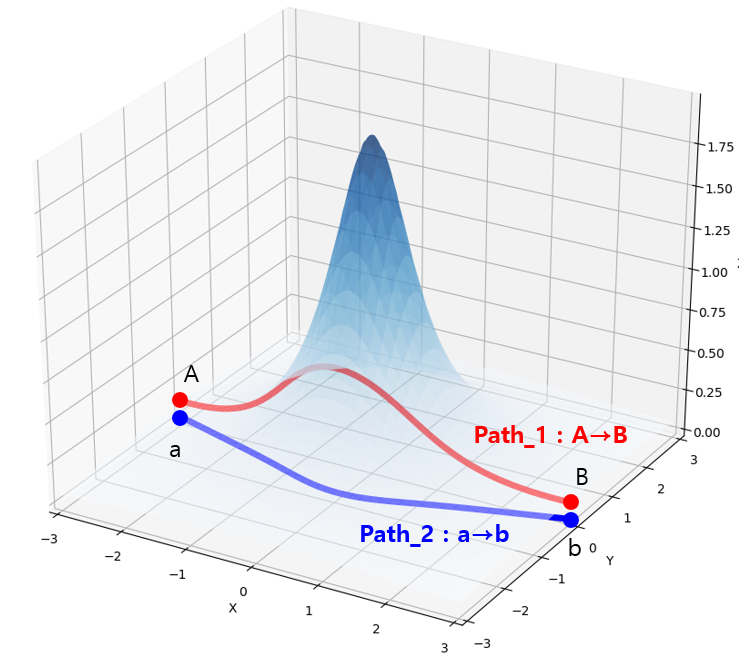
산을 따라서 ($z = f(x,y)$ 평면을 따라서) 가는 $A \rightarrow B$ 경로 (Path_1)를 이동하는 거리를 구하는 것이나, 위 메트릭을 이용하여 $x-y$ 평면에 사영된 산을 따라서 가는 $a \rightarrow b$ 경로 (Path_2)를 이동하는 거리를 구하는 것이나 그 값은 같습니다.
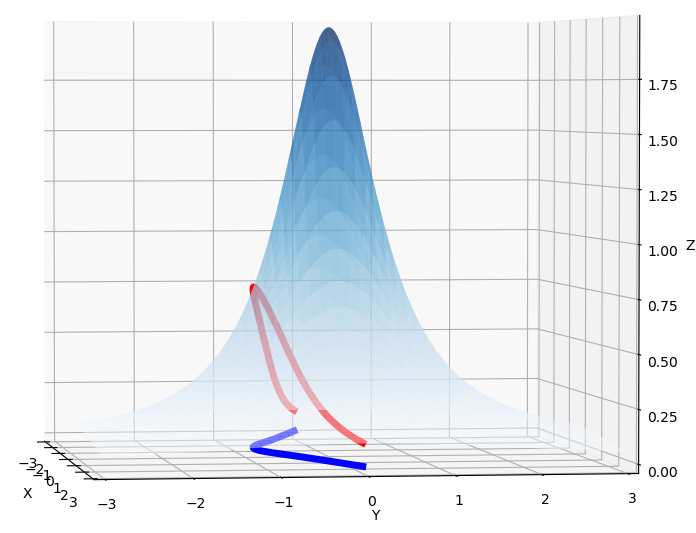
3차원 공간상에서 이동하는 경로 Path_1과 2차원 평면상에서 이동하는 경로 Path_2를 좀 더 잘 보이게 하기 위해서 3차원 그래프를 그리는 축을 변경하였습니다. 요약하자면, 등산객은 실제로 3차원 공간에서 이동하기 때문에 (물론 $z = f(x,y)$ 평면에서 움직여야 합니다. 하늘을 날 수는 없습니다), 3차원 공간에서 정의된 경로 대응 되는 길이를 구해야 하는데, 이는 메트릭이 위와 같이 주어진 2차원 공간에서 정의된 경로에 대응 되는 길이는 구하는 문제로 바꿀 수 있습니다. 문제의 차원을 3차원 문제에서 2차원 문제로 바꿔 생각 할 수 있는 것 입니다. 즉, $z$축이 없는 것 처럼 생각할 수 있습니다.
혹은 반대로, 메트릭이 위와 같이 주어진 2차원 공간에서 경로(곡선)의 길이를 구하는 문제가 주어졌다면, 이에 대응하는 3차원 공간에서 경로(곡선)의 길이를 구하는 문제로 생각할 수 도 있습니다. 3차원 공간에서 곡선의 길이는 우리가 익히 생각하는 $ds = \sqrt{dx^2 + dy^2 + dz^2}$로 주어진 길이 입니다. 이 경우는 메트릭이 $g(x)_{xx} = g(x)_{yy} = g(x)_{zz} = 1, g(x)_{xy} = g(x)_{yz} = g(x)_{zx} = 0$ 으로 주어졌을 때, 이 메트릭에 의한 길이를 구하는 것과 같습니다. 차원을 하나 더 올리거나, 혹은 차원을 하나 더 낮추거나... 필요에 따라서 문제(생각)를 달리 할 수 있습니다.
측지선
이제 최단 경로를 구해 보겠습니다. 페르마의 원리에 따라서 빛의 경로를 구한것과 마찬가지로 이는 변분법 문제인데,
$$0 = \delta \int_{a}^{b} ds = \delta \int_{a}^{b} \sqrt{(1+f_x^2)dx^2 + (1+f_y^2)dy^2 + (2f_xf_y)dxdy} $$
인 경로를 찾는 문제 입니다. $x-y$ 평면에서의 경로를 매개 변수 $t$를 도입해 표현하면 $(x,y) = (x(t), y(t)), t \in [t_a, t_b]$가 되고, 위 적분식은
$$0 = \delta \int_{t_a}^{t_b} \sqrt{(1+f_x^2)v_x^2 + (1+f_y^2)v_y^2 + (2f_xf_y)v_xv_y}dt$$
로 표현할 수 있게 됩니다. 여기서 $v_x = \frac{dx}{dt}, v_y = \frac{dy}{dt}$ 입니다. 일반적인 메트릭으로 쓰면,
$$0 = \delta \int_{t_a}^{t_b} \sqrt{g(x,y)_{xx}v_x^2 + g(x,y)_{yy}v_y^2 + 2g(x,y)_{x,y}v_xv_y}dt$$
가 됩니다. 위 변분법 문제를 풀면, 일반적인 메트릭 $g_{i,j}$가 정의된 공간에서의 최단 경로를 구할 수 있습니다. 이 최단 경로를 측지선(geodesic) 이라고 합니다. 영어 geodesic은 geodesy에서 온 말로, geodesy는 지구 과학의 한 분야로 지구를 정확하게 측량하는 분과를 뜻 한다고 합니다. geodesic의 원래 의미는 지구 상의 두 점을 잇는 가장 짧은 경로를 뜻 했는데, 이 의미가 수학에서 좀 더 일반화 되어 사용되고 있습니다.
측지선 방정식
위 측지선을 구하는 변분법 문제에 대한 오일러-라그랑쥬 방정식은
$$\frac{d^2x^{\lambda}}{dt^2} + \Gamma^{\lambda}_{\mu \nu} \frac{dx^{\mu}}{dt} \frac{dx^{\nu}}{dt} = 0$$
이 됩니다. 여기서 그리스 문제 $\lambda, \mu, \nu$는 $x, y$를 표현하기 위해 도입된 인덱스로 당연히 $x^1 = x, x^2 = y$가 됩니다. 알파벳 $a, b, c$ 혹은 $l,m,n$ 혹은 $p,q,r$를 이용하여 표현해도 되지만 전통적으로 그리스 문제를 사용합니다. 아인슈타인의 더하기 표현법을 사용하였는데 특정 그리스 문자가 위, 아래 인덱스로 중복되어 나오는 경우 $1, 2$ 를 대입하면서 더하는 것을 의미합니다. $\Gamma^{\lambda}_{\mu \nu}$ 는 크리스토펠 심볼(Christoffel symbol)로,
$$\Gamma^{\lambda}_{\mu \nu} = \frac{1}{2} g^{\lambda \alpha} \Big( \partial_\mu g_{\alpha \nu} + \partial_\nu g_{\alpha \mu} - \partial_\alpha g_{\mu \nu} \Big)$$
입니다. 이를 측지선 방정식 (geodesic) 이라고 합니다. 말 그대로 이 방정식을 풀면, 측지선을 구할 수 있는 것 입니다. 여기서 $\partial_\mu$ 는 $x^{\mu}$의 편미분을 의미 합니다. 매우 복잡하고, 인덱스가 많아서 여러번 더하기를 해야하는 계산이지만 어쨌든 $x, y$에 대한 위 미분방정식을 풀면 일반적인 메트릭이 정의된 공간에서의 측지선을 구할 수 있습니다. 2계 미분방정식이기 때문에 경계조건이 필요한데, 보통의 경우에는 우리의 문제에서와 같이 시작점과 끝점이 정해져 있기 때문에, 시작점과 끝점의 좌표를 경계조건으로 이용할 수 있습니다.
"평평한" 공간에서의 측지선
매우 일반적인 경우에 대해 성립하는 복잡한 방정식을 얻었으면, 항상 가장 간단한 경우에 대해서 풀어보고, 우리가 이미 알고 있는 지식과 일치하는지를 확인해야하는데, 가장 간단한 경우는 메트릭 $g_{\mu \nu} =\delta_{\mu \nu} $ 입니다. 이 경우에는 단순히 $ds^2 = dx^2 + dy^2$ 와 같이 피타고라스 정리가 적용이 되는 아주 평범한 공간입니다.
$\Gamma^{\lambda}_{\mu \nu}$는 $g_{\mu \nu}$를 미분해서 얻어지는 값이기 때문에, $g_{\mu \nu} =\delta_{\mu \nu} $ 일때 $\Gamma$의 모든 성분은 0이 되고, 따라서 측지선 방정식은
$$\frac{d^2x^\lambda}{dt^2} = 0$$
와 같이 간단해지며, 위 미분 방정식의 해는 $x(t) = v_x t + x0, y(t) = v_y t + y0$ 즉 직선의 방정식이 됩니다. 이는 공간상의 두 점을 잇는 가장 짧은 경로는 직선이라는 우리의 기본적 지식과 일치합니다. "빛의 경우"를 잊어 버리자고 했는데, 이해를 돕기 위해서 빛의 경우로 설명하면 위 결과는 진공상에서 빛이 직진한다는 것과 같은 결론입니다.
측지선 방정식과 뉴턴 방정식
위 미분 방정식은 $x,y$에 대한 $t$의 2계 미분 방정식으로, 좌변의 두 번째 항을 우변으로 이항하고, 매개변수로 사용한 $t$를 "시간"으로 이해한다면,
$$\frac{d^2x^{\lambda}}{dt^2} =-\Gamma^{\lambda}_{\mu \nu} \frac{dx^{\mu}}{dt} \frac{dx^{\nu}}{dt}$$
이 됩니다. 이는 곧 뉴턴의 운동 법칙과 같은 형태의 식이 됩니다. 질량이 $1kg$의 물체를 생각하면 우변에 있는 $-\Gamma^{\lambda}_{\mu \nu} \frac{dx^{\mu}}{dt} \frac{dx^{\nu}}{dt}$를 "힘"으로 해석할 수 있습니다. 바로 앞 문단에서 살펴본 특수항 경우에는 $\Gamma$의 모든 성분이 0이 되기 때문에 "힘"이 0이 되고 "힘"이 0이 때, 물체는 등속 직선운동을 하게 됩니다. 일반적인 메트릭 $g_{\mu \nu}$ 인 경우, $\Gamma$의 성분은 0이 아니게 되고, "힘"은 위치와 속도에 따라서 바뀌게 됩니다. 실제로 입자에 작용하는 힘은 없지만, 메트릭값과 메트릭값의 변화 때문에 "힘"이 작용하는 것 처럼, 입자의 진행 방향(속도)는 시시각각 바뀌게 됩니다.
구체적인 메트릭에 대한 측지선 방정식의 풀이
측지선을 구하는 방정식을 구했으니, 이제 구체적인 $g_{\mu \nu}$가 주어졌을 때, 두 점을 잇는 측지선을 구해 보고 싶습니다. 이 포스팅의 길이가 평소 다른 포스팅의 길이 보다 무척 길어졌으니, 이 내용에 대해서는 다음 포스팅에서 다루도록 하겠습니다.
'수학' 카테고리의 다른 글
| 무작위 걸음(랜덤 워크 random walk) 102 : 앙상블 평균과 몬테 카를로 시뮬레이션 (1) | 2022.05.01 |
|---|---|
| 무작위 걸음(랜덤 워크 random walk) 101 : 파이썬 프로그램으로 구현 (0) | 2022.04.29 |
| 159종의 띠부띠부씰을 다 모으려면 포켓몬빵 몇 개를 사야 할까? 쿠폰 콜렉터 문제 (4) | 2022.03.25 |
| 우도 함수(가능도 likelihood function)의 이해 (3) | 2021.12.27 |
| 신개선(Involute cuve, 인벌루트 곡선)의 정의와 파이썬 프로그래밍을 통해 그려보기 (1) | 2021.11.06 |



