우도 함수(가능도 함수로 번역되기도 하고, 영어로는 likelihood function 이라 합니다)는 실현된 데이터(혹은 관찰된 데이터 observed data)로 부터 특정 통계 모델의 적합성을 확인하는데 주로 이용됩니다. 실현된 데이터를 $y$라고 하고, 특정 통계 모델을 $\theta$라고 표현했을 때, 우도 함수는 $P(y | \theta)$로 정의되는 값 입니다. 이렇게만 쓰면 우도 함수에 대해서 처음 접하신 분이라면 이해가 쉽지 않을 텐데, 가장 간단한 예시를 통해서 우도 함수가 무엇인지, 어떻게 계산을 하는지, 그리고 어떻게 이용될 수 있는지에 대해서 알아 보도록 하겠습니다.
우리가 던진 동전은 어떤 "모양"일까?
동전 던지기를 해서 앞면 혹은 뒷면이 나오는 횟수를 기록했다고 하겠습니다. 만일 앞면과 뒷면이 나올 확률이 정확히 반반인 공정한 동전이라면 전체 던진 횟수에서 앞면이 나온 횟수가 전체의 $\frac{1}{2}$, 뒷면이 나온 횟수가 전체의 $\frac{1}{2}$이 될 것 입니다.
그런데, 공정하지 않은 동전이 있다고 가정하겠습니다. 모양이 정확히 동전 모양이 아니거나 밀도가 달라서 앞면 혹은 뒷면 중에서 어느 한 면이 나올 가능성이 더 높다고 가정하겠습니다. 이 동전에서 각 면이 나올 확률을 추론하고 싶습니다. 그렇다면 어떻게 해야할까요?
방법은 그져 어려번 던져 보는 수 밖에 없습니다. 만일 동전을 100번 던졌을 때, 앞면이 70번, 뒷면이 30번 나왔다고 가정해 보겠습니다. 이를 편의상 $y = \{70, 30\}$ 이라고 하겠습니다. 물론, 시행의 순서에 따라서 $y = \{H, T, H, T, T....\}$와 같이 수열로 표현할 수 도 있지만, 던진 순서에 따라서 확률이 바뀌지 않는다고 가정한다면, 각 면이 나온 총 횟수만일 기록하여도 충분합니다. $y = \{70, 30\}$가 실현됐다면, 우리는 $P_H = 0.7, P_T = 0.3$이라고 할 것 입니다. 여기서 $P_H$는 앞면(Head)의 확률, $P_T$는 뒷면(Tail)의 확률 입니다. "왜 $P = \{ 0.7, 0.3\}$ 이라고 생각하느냐?" 라고 묻는다면, "그냥 그게 가장 그럼직 한 것 같아" 라고 답할 것 입니다. 이걸 한 번 수학적으로 분석해 보도록 하겠습니다.
가능도 계산
위에서와 같이 우리가 던진 동전에서 앞면이 나올 확률을 $P_H$, 뒷면이 나올 확률을 $P_T$라고 하겠습니다. 확률의 성질상 $P_T = 1 - P_H$, $0 \le P_T \le 1$이 됩니다. 이 때, 앞면이 70번, 뒷면이 30번 나올 확률을 구해보겠습니다. 이 확률을 구하는 것은 고등학교 시절 "확률과 통계" 시간에 한 번쯤은 해 봤을 텐데요,
(1) 특정한 순서로 앞면이 70번, 뒷면이 30번 나오게 되는 확률
(2) 앞면이 70번, 뒷면이 30번 나오게 되는 순서(방법)의 경우의 수
(1), (2)를 곱해 주면 됩니다.
(1) 구하기가 매우 쉬운데, $P_H^{70} \cdot P_T^{30}$ 입니다.
(2)는 100개의 H, T를 줄 세우는 방법 $100!$ 개를 우선 구하고, 이 중에서 H끼리 순서를 바꾸는 것은 의미가 없고, 또한 T끼리 순서를 바꾸는 것은 의미가 없기 때문에 이 두 수의 곱으로 나눠 준 값이 총 경우의 수가 됩니다. 즉 $\frac{100!}{30! \cdot 70!}$ 이 됩니다. 따라서 원래 구하고자 했던 앞면이 70개, 뒷면이 30개가 나올 확률은
$$P =\frac{100!}{30! \cdot 70!} P_H^{70} \cdot P_T^{30} $$
가 됩니다. $P_T = 1 - P_H$을 대입하여, 위 확률을 $P_H$의 함수로 나타내면,
$$P(P_H; 70, 30) =\frac{100!}{30! \cdot 70!} P_H^{70} \cdot (1-P_H)^{30} $$
가 됩니다. 특정한 앞/뒷 면의 분포 (70, 30)에 대한 계산을 한 것 이기에 이를 강조하기 위해서 확률(함수) $P$의 인수에 ";70, 30"을 강조하여 표현하였습니다.
이 확률은 매우 큰 숫자 $\frac{100!}{30! \cdot 70!}$와 매우 작은 숫자 $P_H^{70} \cdot (1-P_H)^{30}$가 곱해진 숫자이기에 이 확률을 그대로 다루는 것은 조금 불편합니다. 따라서 이 숫자에 로그$\log$를 취하곤 하는데, 로그 함수는 단조 증가 함수로 인수의 순서(대소 관계)와 로그를 취한 함수의 순서(대소 관계)가 보존된다는 장점이 있습니다. 로그 확률(확률에 로그를 취한 값)은
$$\log P = \log 100! - \log70! -\log30! + 70 \log P_H + 30 \log(1-P_H)$$
가 됩니다.
가장 "그럼직한" P_H 는?
동전의 앞면이 나올 확률을 $P_H$라고 할 때, $\{70, 30\}$과 같은 분포가 나오는 확률을 위에서 구해 봤습니다. 이 로그 확률을 $P_H$의 함수로 그래프를 그리면 다음과 같습니다.
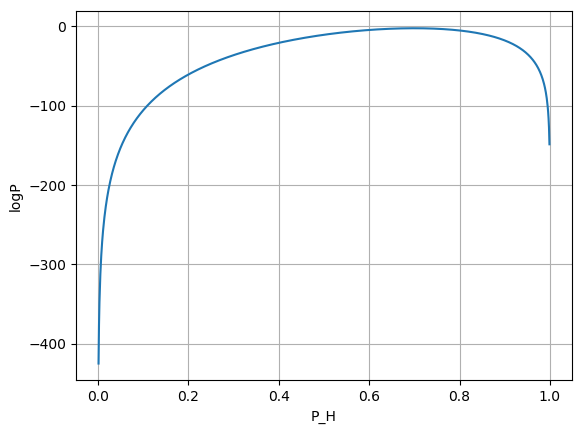
$\log P$가 최대값을 갖는 범위를 확대해서 그리면,
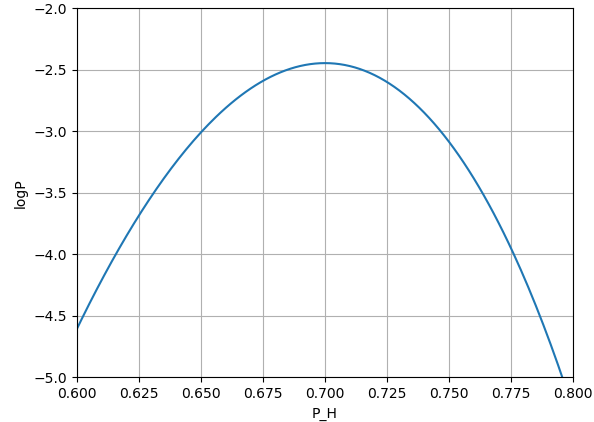
와 같습니다. $\log P(P_H)$ 함수는 $P_H = 0.7$에서 최대값을 갖고, $P_H$가 커지거나, 작아지면 함수값이 작아지게 됩니다. $P_H = 0.7$은 앞면이 나온 빈도와 동일합니다!
$P_H = 0.1$ 인 경우에 $\{70, 30\}$이 실현될 로그 확률은 -105.7로 확률값으로 바꾸면, $P = 1.24 \times 10^{-46}$ 입니다. 즉, 실제로 $P_H = 0.1$인 경우에 $\{70, 30\}$이 실현될 수 있지만, 그 확률은 매우 매우 매우 희박한 것 입니다. 따라서 우리가 던진 동전이 $P_H = 0.1$인 동전이라고 주장하는 것은 매우 무리 입니다. 우리의 관찰이 $1.24 \times 10^{-46}$ 라는 희박한 확률이었는데, 이것이 실제로 일어났다고는 그 누구도 믿어 주지 않을 것 입니다.
$P_H = 0.7$ 인 경우에 $\{70, 30\}$이 실현될 로그 확률은 -2.444로 확률값으로 바꾸면, $P = 0.087$ 입니다. $8.7 \%$라는 그지 크지 않은 확률이긴 하지만, 나름 실현이 가능한 확률이며, $P_H$를 바꿔가면서 확률을 계산했을 때, 가장 실현 가능성이 높은 확률입니다. 따라서 우리가 던진 동전이 $P_H = 0.7$인 동전이라고 주장하는 것은 다른 $P_H$의 확률이라고 주장하는 것 보다 훨씬 더 타당한 주장이 됩니다. $P_H = 0.69$, $P_H = 0.71$ 인 동전의 경우 $\{70, 30\}$의 빈도가 실현될 확률은 각각 $8.476\%, 8.471 \%$ 로 $P_H = 0.70$ 동전의 확률과 거의 비슷합니다. 그러나 어쨋뜬 $P_H = 0.70$ 동전의 확률이 조금 더 높기 때문에, 우리가 던진 동전의 $P_H$는 $0.7$ 이었다고 주장하는 것이 가장 그럼직 합니다.
위 과정을 일반화 하여 표현하면
위에서는 간단하게 설명을 하기 위해서 쉬운 구체적인 예시를 들었습니다. 위 과정을 일반화하면 다음과 같습니다.
- $\{70, 30\}$ : 실제로 일어난 현상(observed data)의 표현 입니다. 보통 $y$로 씁니다.
- $P_H, P_T$ : 통계 모델, 위 문제에서는 동전의 모델, 을 구성하는데 사용한 파라미터 값 입니다. 보통 $\theta$로 표현하는데, 갯수가 2개 이상인 경우에는 벡터 표시법을 빌려서 $\vec{\theta}$와 같이 표현합니다.
- $P_H$가 정해져 있을 때, $\{70, 30\}$가 실현될 확률 : $\vec{\theta}$가 주어진 상황에서 $y$가 구현될 확률로 조건부 확률 $P(y | \vec{\theta}) $라고 쓸 수 있습니다. 이 값을 우도(혹은 가능도) 라고 하고, $\mathcal{L}(\vec{\theta}|y)$ 로 표시합니다. 이 값은 $\vec{\theta}$의 함수입니다. $\mathcal{L}(\vec{\theta}|y) = P(y | \vec{\theta})$ 인데, "우도"라는 것을 강조하기 위해서 멋들어진 대문자 L 를 이용하여 표현합니다.
- 가장 그럼직한 $P_H = 0.7$ : $\mathcal{L}(\vec{\theta}|y)$가 최대값을 갖도록 하는 $\theta$값 입니다. $\hat{\theta} = \arg \max \mathcal{L}(\vec{\theta}|y)$ 로 표현 할 수 있습니다. 우도 함수가 최대가 되게 하는 통계 모델의 파라미터 $\theta$를 찾고, 이 값을 통계 모델의 파라미터 값으로 여기는 방법을 최대 우도법(maximum likelihood estimation)이라고 합니다. 최대 우도법은 통계 모델을 추정하는 매우 중요한 방법 중에 하나이니, 다음 포스팅을 통해서 조금 더 자세하게 알아 볼 것 입니다.
다시 한 번 설명하면, 우도(가능도, likelihood)는 "특정한 현상이 일어 났다고 할 때, 특정 통계 모델 하에서 이 현상이 일어날 확률" 을 뜻 합니다. 위 예시를 통해 설명하면
특정한 현상 = $\{70, 30\}$ 이라는 앞면, 뒷면의 횟수
특정 통계 모델 = 동전의 앞면이 나올 확률은 $P_H$, 뒷면이 나올 확률을 $1-P_H$라고 동전을 모델링 하는 것
이 현상이 일어날 확률 = $P =\frac{100!}{30! \cdot 70!} P_H^{70} \cdot P_T^{30} $
가 되는 것 입니다.
통계 모델이 확률 밀도 함수로 주어졌다면
위 예시에서 통계 모델은 확률 질량 함수(probability mass function)를 통해 정의 되었습니다. 즉, 표본 공간 (sample space) 은 $\{ H, T \}$와 같이 원소의 갯수가 유한하며 각 원소마다 $P_H, P_T$를 지정할 수 있었습니다. 만일 통계 모델의 표본 공간이 연속적인 값을 갖게 된다면 확률 질량 함수가 아닌 확률 밀도 함수(probability density function)를 사용하여 우도를 정의할 수 있습니다. 이 경우에는 확률 질량 함수 자리에 확률 밀도 함수를 써주면 되는데, 구체적인 예들들어 보도록 하겠습니다.
마트에서 귤을 10개 샀는데, 귤의 무게의 분포가 평균이 $\mu$, 표준편차가 $\sigma$인 정규 분포를 따른다고 하겠습니다. 즉 하나의 귤에 대해서 이 귤의 무게는 확률 밀도 함수 $\frac{1}{\sqrt{2\pi}\sigma} e^{-\frac{(m-\mu)^2}{2\sigma^2}}$에 의해 주어집니다. 이 때, 10개의 귤의 무게가 $y = \{ m_1, m_2, ..., m_{10}\}$으로 주어졌을 때, 우도 함수는
$$\mathcal{L} = \prod_{i=1}^{10} \frac{1}{\sqrt{2\pi}\sigma} e^{-\frac{(m_i-\mu)^2}{2\sigma^2}} = \Big( \frac{1}{\sqrt{2\pi}\sigma}\Big)^{10} \exp\Big( -\sum_{i=1}^{10} \frac{(m_i-\mu)^2}{2\sigma^2} \Big)$$
가 됩니다. 역시나 이 전의 예시 처럼 $\vec{\theta} = (\mu, \sigma)$를 이용하여 $\mathcal{L}(\vec{\theta}|y)$ 같이 표현 할 수 있습니다.
'수학' 카테고리의 다른 글
| 공간에 따라 굴절률이 달라지는 매질에서 빛의 경로의 일반화 : 측지선(geodesic)과 측지선 방정식(geodesic equation) (1) | 2022.04.23 |
|---|---|
| 159종의 띠부띠부씰을 다 모으려면 포켓몬빵 몇 개를 사야 할까? 쿠폰 콜렉터 문제 (4) | 2022.03.25 |
| 신개선(Involute cuve, 인벌루트 곡선)의 정의와 파이썬 프로그래밍을 통해 그려보기 (1) | 2021.11.06 |
| 수학적 최적화 수치해법으로 풀어보는 변분법 문제 : 최단 하강 곡선 (1) | 2021.11.04 |
| 가우스 구적법 (Gauss Quadrature (0) | 2021.10.03 |



