변분법은 주어진 범함수의 값을 극대 혹은 극소로 만드는 범함수의 입력 변수인 함수를 찾는 방법입니다. 조금 형식적으로 쓴다면, 함수
$$f(x) : x \ \in [a, b] \rightarrow y \in V \subset \mathbb{R} $$
가 주어졌을 때, 어떠한 범함수 $J[f(x)]$에 대하여 $J[f(x)]$가 극대 혹은 극소를 갖게 하는 $f(x)$를 찾는 것 입니다. 보통의 경우 극소 더 정확히는 최소값을 찾기 때문에, 앞으로는 별다른 이유가 없다면 그냥 최소값을 찾는 문제를 생각하도록 하겠습니다.
구체적으로 범함수 $J[f(x)]$가 $f(x)$와 $f'(x)$의 함수 $L\big( f(x), f'(x) \big)$의 적분으로 주어졌을 때, 즉
$$J[f(x)] = \int_{a}^b L\big(f(x), f'(x), x\big)dx$$
와 같은 형태일 때, 오일러-라그랑쥬 방정식을 풀어서 $f(x)$를 구하게 됩니다. 오일러-라그랑쥬 방정식은 함수 $f(x)$에 대한 미분 방정식이 되고, 해석적인 방법으로 풀 수 있다면 해석적인 방법으로, 그렇지 못 하다면 수치해법으로 문제를 풀 수 있습니다. 미분 방정식을 수치해법인 방법으로 푸는 것에 대해서는 지난 여러번의 포스팅을 통해서 설명한 바 있습니다.
이번 포스팅에서는 이 문제를 조금 다른 방식으로 풀어 보려고 합니다. 즉, 오일러-라그랑쥬 방정식을 풀기 보다는 범함수를 직접적으로 최소하 하는 방식의 해법을 통해 해 $f(x)$를 구할 것 입니다.
수치해법의 시작은 연속된 값을 불연속화 하는 것
지난 여러번의 수치해법을 다룬 포스팅에서와 같이 수치해법으로 문제를 풀 때, 가장 먼저하는 것은 연속된 값을 불연속된 값의 집합으로 만드는 것 입니다. 즉 구간 $x \in [a,b]$에서 정의된 $f(x)$에 대해서, 구간 $[a, b]$을 $N$개의 조각으로 나누고 각 조각의 값을 $x_n = a + \frac{b-a}{N}n, n=0, 1, ..., N$와 같이 표현할 수 있습니다. 그리고 각 $x_n$에서의 함수값 $f(x_n)$을 편의상 $f_n$이라고 쓸 수 있습니다. 함수 $f(x)$의 미분 $f'(x)$ 역시 비슷한 방법으로 쓸 수 있습니다. 이 과정에서는 작지만 유한한 크기의 $h$를 통해서 $f'(x) \approx \frac{f(x+h) - f(x)}{h}$와 같이 근사 할 수 있습니다. 여기서 $h = \frac{b-a}{N}$으로 한다면, $x= x_n$에서 $f'(x_n) \approx \frac{f(x_{n+1}) - f(x_n)}{h}$와 같이 근사할 수 있고, $f'_n = \frac{f_{n+1} - f_n}{h} = (f_{n+1} - f_n) \frac{N}{b-a}$ 와 같이 $f'_n$을 $f_{n+1}, f_n$의 값으로 표현할 수 있습니다.
따라서, 범함수 $J[f(x)]$를
$$J[f(x)] = \int_{a}^b L\big(f(x), f'(x), x\big)dx \approx \int_a^b \tilde{L} \big( \{f_n | n=0, 1, 2, ..., N\} \big) dx$$
와 같이 근사 할 수 있습니다. 여기서 $\tilde{L} \big( \{f_n | n=0, 1, 2, ..., N\}$는 $L\big(f(x), f'(x), x\big)$를 위에서 설명한 근사를 통해서 표현한 함수 입니다. $L$의 구체적인 형태에 따라서 다르겠지만, $\tilde{L}$은 $f_0, f_1, f_2, ..., f_N$의 함수가 됩니다. 결과적으로 최소화 해야하는 목적 함수 $J$를 $f_n, n=0, 1, 2, ..., N$의 함수 $J(f_0, f_1, f_2, ..., f_N)$와 같이 쓸 수 있고, $J(f_0, f_1, f_2, ..., f_N)$를 일반적인 수하적 최적화 알고리듬을 통해서 최적화(최소화)하게 되면 $J$의 최소값과 이때의 함수값 $f(x_n) = f_n$을 구할 수 있게 됩니다.
구체적인 문제를 통해서 위 과정을 수행해 보자
단순히 형식적으로 설명한 하면 이해가 어려운 경우가 많습니다. 따라서 간단하지만 구체적인 예시를 들면 매우 좋은데요, 변분법 문제 중에서 가장 유명한 문제는 최단 하강 곡선을 구하는 문제를 통해서 위 과정을 설명해 보도록 하겠습니다. 최단 하강 곡선 문제는 굳이 여기서 설명하지 않아도 될 정도로 잘 알려진 문제인데요,
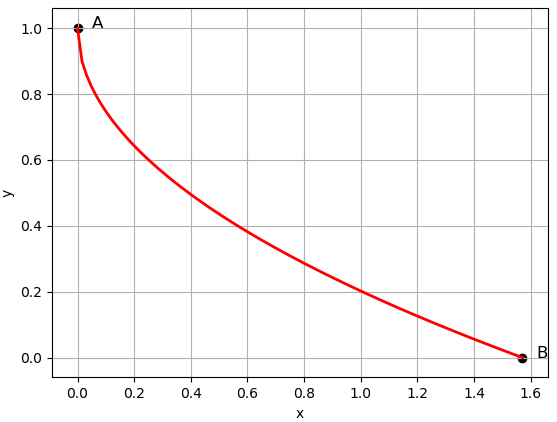
위 그림에서와 같이 $A$에 놓여진 질점이 중력의 영향을 받으면서 곡선을 따라 $B$ 위치로 내려갈 때, 곡선의 형태가 어떤 형태이어야 가장 빠르게 $B$로 도착할 수 있는지를 찾는 문제 입니다. 곡선의 형태는 함수 $y = f(x)$로 놓을 수 있고, $A \rightarrow B$ 의 시간은 고전 역학의 법칙에 따라서,
$$T = \int_{A}^{B} \frac{\sqrt{1 + f'(x)^2}}{\sqrt{1 - f(x)}} dx$$
가 됩니다. 보다 정확히 하려면 중력 상수, 입자의 질량 등 물리 상수가 비례상수로 있어야 하지만, 중요한 값이 아니기 때문에, 모두 생략했습니다. 포스팅의 앞 부분에 쓴, 일반적인 변분법의 문제와 대응한다면, $L(f, f') = \frac{\sqrt{1 + f'(x)^2}}{\sqrt{1 - f(x)}}$이 됩니다.
위 그림에서는 구체적으로 시작점 $A = (0, 1)$, 도착점 $B = (\pi/2, 0)$ 로 하였습니다.
이제 입력 변수 $x$를 불연속화 하고, 이를 통해서 $\tilde{L}(f_0, f_1, f_2, ..., f_N) $을 구해보도록 하겠습니다.

위 그림은 $f(x)$의 정의역 $[0, \pi/2]$를 $N=3$ 조각으로 나눈 예시 입니다. 즉, $x_n = \frac{\pi/2}{N}n, n=0, 1, 2, 3$와 같이 나타낼 수 있고, $(x_0, f(x_0)) = (x_0, f_0) = A$, $(x_3, f(x_3)) = (x_3, f_3) = B$ 가 됩니다. 그리고 중간에 $(x_1, f_1), (x_2, f_2)$를 표시하였습니다. 연속적인 공간을 $N=3$조각으로 불연속화 하였고, 따라서 점선으로 표시한, 원래는 곡선이던 $f(x)$는 실선으로 표시한 부분적인 선분의 합으로 표현됩니다. 정의역 공간을 불연속화 했기 때문에, 함수 역시 부드러운 곡선에서 부분적으로 선분인 형태로 바뀐 것 입니다. 즉, 우리의 문제는 $A \rightarrow B$를 연결하는 곡선을 찾는 것이 아니라, $A \rightarrow f_1 \rightarrow f_2 \rightarrow B$ 를 연결하는 부분적인 선분의 합을 찾는 문제로 바뀌었습니다.
$(x_n, f_n)$와 $(x_{n+1}, f_{n+1})$ 사이의 선분의 식은 $f(x) = \frac{f_{n+1} - f_n}{x_{n+1} - x_n} (x- x_{n}) + f_n$이 되고, 따라서 $A \rightarrow B$ 시간 $T_{AB}$는
$$T_{AB} = \sum_{n=0}^{2}\int_{x_n}^{x_{n+1}} \frac{\sqrt{1+(\frac{f_{n+1} - f_n}{x_{n+1} - x_n})^2}}{\sqrt{1-\big(\frac{f_{n+1} - f_n}{x_{n+1} - x_n} (x- x_{n}) + f_n\big)}}dx$$
가 됩니다. 위 식의 피적분 함수의 분자는 $x$와 무관한 상수이기 때문에 적분 기호 밖으로 바로 나올 수 있고,
$$\int \frac{1}{\sqrt{ax + b}}dx = \frac{2}{a} \sqrt{ax +b}$$
를 이용하여 위 식을 정리하면,
$$T_{AB} = T_{AB}(f_0, f_1, f_2, f_3)= 2 \sum_{n=0}^{2} \sqrt{1 + \big( \frac{x_{n+1} - x_n}{y_{n+1} - y_n} \big)^2} \big( \sqrt{1-f_{n+1}} - \sqrt{1-f_n} \big)$$
를 얻습니다. 위 $T_{AB}$가 $f_0, f_1, f_2, f_3$에 대한 함수라는 것을 강조하기 위해서 $T_{AB}(f_0, f_1, f_2, f_3)$라고 썼습니다. 물론, $f_0 = 1, f_3 = 0$와 같이 문제의 초기값으로 고정 되었기 때문에, 실제로 $T_{AB}$는 $f_1, f_2$의 함수가 됩니다.
수학적 최적화 알고리듬을 이용하여 $T_{AB}(f_1, f_2)$를 최소화 하자
위 $T_{AB}(f_1, f_2)$는 2변수 함수이고, 해석적으로 미분이 가능하기 때문에, 해석적인 방법으로 문제를 풀어도 되지만, 매우 번거롭고 귀찮습니다. 그리고 무엇 보다도 최종적으로는 $N \rightarrow \infty$를 해야하기 때문에(물론 수치해법에서는 무한대를 가정할 수 없으므로, 매우 큰 숫자 입니다), 컴퓨터 프로그래밍을 통해서 푸는 것이 좋습니다. 저는 파이썬 프로그래밍을 통해서 해를 구하였습니다. 파이썬의 scipy 라이브러리중 scipyt.optimize.minimize를 사용하였습니다. 다양한 최적화 알고리듬 중에서 SLSQP를 사용하였습니다. 최적화 알고리듬은 문제의 상황에 적절한 것을 선택하는 것이 중요한데, 이 문제의 목적함수 $T_{AB}(f_1, f_2)$는 그리 복잡한 형태의 함수가 아니기 때문에, 아무 최적화 알고리듬을 선택하여도 결과는 같습니다.
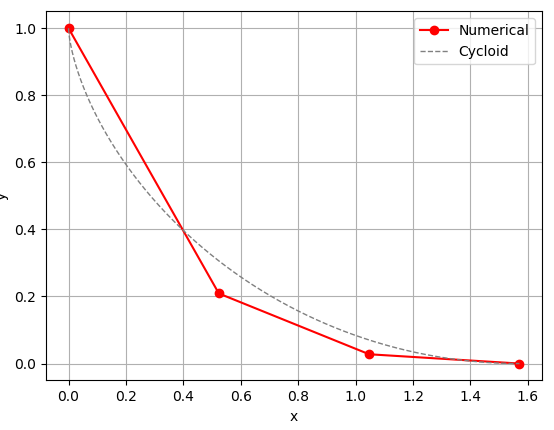
해는 위와 같습니다. 비교를 위해서 해석적인 해인 사이클로이드 곡선을 점선으로 그렸습니다. 붉은색 실선으로 표현한 $N=3$으로 곡선을 분절화한 선분들의 연결이 사이클로이드 곡선과 유사한 모양이 되었습니다.
앞서 언급했던 것과 같이 $N \rightarrow \infty$가 되면 해석적인 해인 사이클로이드와 같아져야 합니다. 이를 얻기 위해서 이번에는 $N=30$으로 값을 키워 보도록 하겠습니다.

결과는 위 그래프와 같습니다. 수치해법으로 얻은 곡선이 사이클로이드 곡선과 거의 유사해 졌습니다. 특히 $x \gt 1$ 부근에서는 사이클로이드 곡선과 거의 차이를 확인하지 못 할 정도로 같아졌습니다.
https://www.youtube.com/watch?v=81-TO6HV3mc
SLSQP 알고리듬을 이용한 수학적 최적화 계산에서 각 단계(iteration)별로 얻어지는 곡선의 개형 변화는 위 동영상과 같습니다. 최적화를 시작 할 때는 $A \rightarrow B$를 직선으로 잇는 함수에서 시작 했으나, 최적화 과정이 진행됨에 따라서 해석적인 해인 사이클로이드 곡선과 점차적으로 닮아감을 볼 수 있습니다. $B$근처의 곡선보다 $A$근처의 곡선이 사이클로이드 곡선에 더 빨리 수렴해가는데, $B$근처의 함수값이 변화하는 것 보다는 시작점에 가까운 $A$ 근처의 함수값이 변화하는 것이 $T_{AB}$를 줄이는데 보다 이득이기 때문에 $A$근처의 곡선이 보다 빨리 사이클로이드 곡선과 가까워 집니다.
조금 더 $N$값을 키워 보도록 하겠습니다.

$N=100$의 경우 입니다. $N=30$의 경우에서는 $x \approx 0$ 근처에서 사이클로이드 곡선과 수치해법으로 얻은 곡선의 불일치를 볼 수 있었는데, 이 경우에는 수치해법으로 얻은 곡선이 거의 완전히 사이클로이드 곡선 위에 놓여져 있게 됩니다.
이상과 같이 아주 간단한 경우에 대해서 수치해법의 방법을 이용하여 변분법 문제를 풀어보았습니다. 앞에서 설명한 것과 같이 변분법 문제를 풀기 위해서는 오일러-라그랑쥬 방정식을 얻고, 그 미분 방정식을 수치적인 해법을 통해서 구할 수 도 있지만, 보다 직접적인 방법으로 수치해법을 적용하여 이번 포스팅에서와 같이 해를 직접 얻을 수 도 있습니다. 어느 방법이 더 효율적이냐는 것은 문제의 상황에 따라서 달라집니다.
변분법의 범위에 있는 문제는 최단 하강 곡선 이외에도 재미난 문제가 엄청 많습니다. 다양한 문제들에 대해서는 다음 포스팅에서 조금씩 더 풀어 보도록 하겠습니다.
'수학' 카테고리의 다른 글
| 우도 함수(가능도 likelihood function)의 이해 (3) | 2021.12.27 |
|---|---|
| 신개선(Involute cuve, 인벌루트 곡선)의 정의와 파이썬 프로그래밍을 통해 그려보기 (1) | 2021.11.06 |
| 가우스 구적법 (Gauss Quadrature (0) | 2021.10.03 |
| 사이클로이드(cycloid) 곡선만이 유일한 등시 곡선(Tautochrone curve)일까? (5) | 2021.09.25 |
| 드럼의 모양을 들을 수 있을까? (Can one hear the shape of a drum?) : (1) 2차원 직사각형 드럼에 대한 예시 (0) | 2021.09.14 |



