최근에, 블로그 댓글을 달아주신 독자분을 통해서 신개선이라는 것을 처음 알게 되었습니다. 궁금해서 약간 더 찾아봤는데, 순수하게 수학적인 연구의 대상이 되기도 하지만, 주로 기어 제작쪽 어플리케이션에 많이 활용된다는 것을 알게 되었습니다. 이번 포스팅에서는 신개선에 대해서 알아보고, 임의의 곡선에 대한 신개선이 어떻게 정의되는지, 그리고 그것을 실제로 구하기(그리기) 위한 파이썬 프로그래밍을 해 보도록 하겠습니다.
인터넷 검색을 하니 신개선이라는 우리말(한자어)로 번역한 단어 보다는 영어 단어를 그대로 음역한 "인벌루트" 라는 말을 더 많이 사용하는 것 같습니다. 그래서 이번 포스팅에서도 그냥 인벌루트 혹은 인벌루트 커브(곡선)이라고 칭하도록 하겠습니다.
한글 위키백과의 신개선 페이지에서 인벌루트 곡선의 정의는 "곡선의 모든 접선 중 적당한 한 점씩을 포함하는 곡면 위에 놓여 있으며 원 곡선의 모든 접선들과는 수직으로 만나는 또다른 곡선이다." 라고 정의가 돼 있습니다. 여러번 읽어 봤는데, 잘 이해가 되지 않습니다. 백문이 불여일견 이라고해서, 설명을 하기 보다는 좋은 예시를 하나 들어보도록 하겠습니다.
https://www.youtube.com/shorts/ZNmr3vYoYJo
위 영상은 원(검은색으로 표시)의 인벌루트 커브(붉은색으로 표시)를 나타낸 것 입니다. 동치인 정의가 여럿 있을 수 있으나, 위 영상과 같이 "어떠한 곡선(위 예시에서는 원)에 실을 감았을 때, 끝 점의 자취(위 예시에서는 붉은색 곡선)"이라고 할 수 있습니다. 반대로 생각하면, 어떤 곡선에 감겨있는 실을 풀었을 때, 끝 점의 자취 라고도 할 수 있습니다. 수학적으로는 정확한 정의가 아닐 수 있으나, 가장 이해하기 쉬운 정의라고 생각합니다.

위 에니메이션에서는 풀려있던 실을 원에다 감는 것을 보여주었는데, 반대로 원에 감겨있던 실을 푸는 과정을 생각해 보겠습니다. 이렇게 생각하는 것이 개념적으로 더 쉽습니다.
점 $A$에 있던 실의 끝점이 풀려서 점 $C$로 이동하였습니다. 인벌루트 커브는 점 $C$의 자취 입니다. 곡선 $AC$의 길이는 당연히 $AB$와 같고, $C$의 위치는 점 $B$에서 원의 접선 방향입니다. 반대로 설명하면, 원 위의 점 $B$의 접선 중에서 점 $B$의 진행 방향(반 시계 방향)과 반대 방향에 점 $C$가 놓이게 되는데, 선분 $BC$의 길이는 곡선 $AB$의 길이와 같게 됩니다.
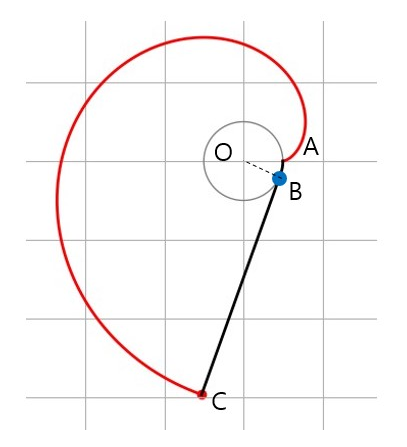
위 그림은 점 $B$가 원을 거의 한 바퀴 돌아서 다시 $A$에 도달하기 직전의 위치 입니다. 위에서 설명한 방식대로 점 $C$의 위치는 점 $B$의 접선 위에 있게 되는데, 곡선 $BC$의 길이는 반 시계 방향으로 거의 한 바퀴 다 돌아온 곡선 $AB$의 길이와 같게 됩니다. 같은 방식으로 임의의 $B$ 위치에 대응되는 $C$를 찾을 수 있고, 이 $C$점을 모두 모아 놓으면 위 붉은색 곡선 처럼 됩니다. 이것이 원의 인벌루트 곡선이 됩니다.

점 $B$가 원주 위를 한 바퀴 돌고 끝난 것이 아니라 한 바퀴 더 돌게 되면 위와 같은 인벌루트 곡선이 얻어집니다. 역시나 점 $C$를 구하는 방식은 같습니다.
평면 위에 놓인 곡선은 1변수 함수로 표현이 가능한데, 즉
$$c : t \in [t_1, t_2] \rightarrow \vec{c}(t) = (x(t), y(t)) \in \mathbb{R}^2 $$
와 같이 쓸 수 있는데, 이 곡선 $\vec{c}(t)$에 대응되는 인벌루트 커브의 방정식은
$$\vec{C}_{t_1}(t) = \vec{c}(t) - \frac{\vec{c}'(t)}{|\vec{c}'(t)|} \int_{t_1}^t |\vec{c}'(\omega)| d\omega$$
로 주어지게 됩니다. 앞에서 예를 들어서 설명한 바와 같이, 점 $C$ ($\vec{C}_{t_1}(t)$) 는 점 $B$ ($\vec{c}(t)$)를 기준으로 점 $B$의 접선($\frac{\vec{c}'(t)}{|\vec{c}'(t)|}$) 상에 놓이게 되는데, 점 $BC$의 길이는 기준점 $A$로 부터 $B$까지의 거리 $AB$ ($\int_{t_1}^t |\vec{c}'(\omega)| d\omega$)가 되기 때문입니다.
위 식에서 분모에 $|\vec{c}'(t)|$가 있기 때문에, 이 값은 $0$이 되어서는 안됩니다.
import numpy as np
import matplotlib.pyplot as plt
### 원을 t로 매개화
t = np.linspace(0, 2*np.pi, 1000)
x, y = np.cos(t), np.sin(t)
### 점A와 점B 사이의 거리 구하기
dx = np.hstack([[0], x[1:] - x[:-1]])
dy = np.hstack([[0], y[1:] - y[:-1]])
ds = np.sqrt(dx**2.0 + dy**2.0)
st = np.cumsum(ds)
### 인벌루트 곡선의 방정식에 따라 인벌루트 곡선 구하기
dt = t[1] - t[0]
vx, vy = dx/dt, dy/dt
ux, uy = vx/np.sqrt(vx**2.0 + vy**2.0), vy/np.sqrt(vx**2.0 + vy**2.0)
p = x - ux*st
q = y - uy*st
#### matplotlib를 이용하여 그래프 그리기
plt.figure(figsize=(8, 8))
plt.plot(x, y, color='black', lw=2)
plt.plot(p, q, lw=2, color='red')
plt.grid()
plt.xlim(-8,8)
plt.ylim(-8,8)
plt.show()파이썬을 이용하여 원의 인벌루트 곡선을 구하는 짧은 코딩을 하였습니다. 위 $x, y$를 정의하는 부분에 임의의 곡선의 매개화 방정식을 넣으면, 임의의 방정식에 대한 인벌루트 곡선을 구할 수 있습니다.
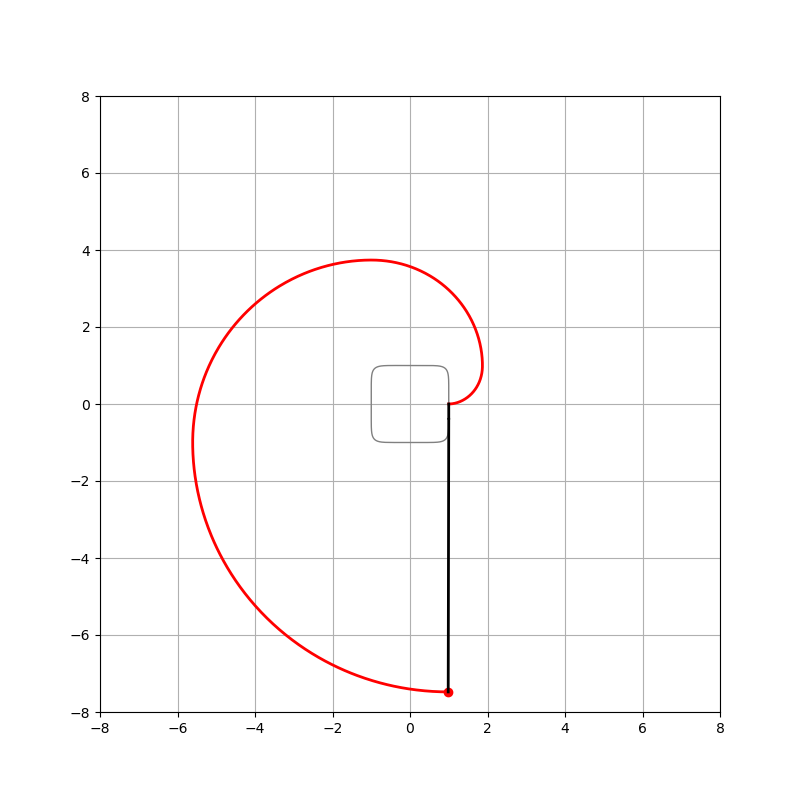

위 예시는 꼭지점 부분이 둥글게 생긴 사각형의 인벌루트 곡선입니다. 이 시각형은 다양한 방식으로 매개화가 가능하겠지만,
x, y = np.sign(np.cos(t))*np.abs(np.cos(t))**0.25, np.sign(np.sin(t))*np.abs(np.sin(t))**0.25를 이용하여 표현하였습니다. 따라서 상하좌우에 직선처럼 보이는 부분은 직선이 아니라 실제로는 곡선인데, 직선 처럼 보이는 것 뿐입니다. 아래 그림은 특정한 점 $B$에 대응되는 점 $C$의 관계를 그린 것 입니다. 원에서 사각형으로 바뀐 것 이외의 차이는 없습니다.
꼭지점이 뾰족한 사각형은 꼭지점 부분에서 $\vec{c}'(t)$를 정의할 수 없기 때문에, 인벌루트 곡선을 구할 수 없습니다. 물론, 위와 같이 꼭지점을 둥글게 만들어서 근사적으로 구할 수 있습니다.
또 다른 유명한 곡선이면서, 이 블로그에도 여러번 소개된 바 있는 사이클로이드 곡선의 인벌루트 곡선을 구해 보도록 하겠습니다.

정확히는 위 그림과 같이 사이클로이드 곡선의 일부가 한 점 $(0,2)$ 에서 맞닫아 있는 곡선의 인벌루트 곡선입니다. 인벌루트 곡선이 시작되는 점은 $(\pi, 0)$ 입니다. 앞에서 도입한 인벌루트 곡선의 방정식에 사이클로이드 곡선을 적절히 대입하면, 아래와 같은 인벌루트 곡선을 얻을 수 있습니다.
https://www.youtube.com/watch?v=UL1sqmwXMuY

최종적인 곡선은 위 그림과 같습니다. 인벌루트 커브로 얻어진 붉은색 곡선은 또 다시 사이클로이드 곡선이 됩니다.
위 영상에서와 같이 실제로 실과 추(점)을 준비하여 두 사이클로이드가 맞닫아 있는 점에 고정하고 진자 운동을 하도록 놓으면 점의 궤적은 붉은색 사이클로이드 곡선과 같이 됩니다. 즉, 점은 중력장 하에서 사이클로이드 곡선상에서 운동을 하게 되고, 사이클로이드 곡선의 특성에 따라서 운동의 주기는 진폭과 상관 없이 항상 같게 됩니다. 공기의 저항에 의해서 진동의 진폭이 줄어들더라도 사이클로이드의 성질 때문에, 운동의 주기가 같아지고 따라서 위와 같은 조건에서 주기 운동을 하는 진자는 항상 주기가 변하지 않기 때문에, 시계의 역할을 할 수 있습니다. 바로 이와 같은 원리로 시간을 측정하는 방법을 1600년대 수학자이자 물리학자인 호이겐스가 고안하였습니다.
'수학' 카테고리의 다른 글
| 159종의 띠부띠부씰을 다 모으려면 포켓몬빵 몇 개를 사야 할까? 쿠폰 콜렉터 문제 (4) | 2022.03.25 |
|---|---|
| 우도 함수(가능도 likelihood function)의 이해 (3) | 2021.12.27 |
| 수학적 최적화 수치해법으로 풀어보는 변분법 문제 : 최단 하강 곡선 (1) | 2021.11.04 |
| 가우스 구적법 (Gauss Quadrature (0) | 2021.10.03 |
| 사이클로이드(cycloid) 곡선만이 유일한 등시 곡선(Tautochrone curve)일까? (5) | 2021.09.25 |



