랜덤 워크
무작위 걸음(랜덤 워크 Random Walk)는 대표적인 확률과정(stochastic process)의 예시로, 연속적인 무작위 수에 의해서 결정되는 확률 공간에서의 "움직임의 경로"에 대해서 다룹니다. (위 첫 문장을 쓰고 지우고를 여러번 반복하였는데) 무작위 걸음은 이에 대해서 길게 설명하는 것 보다는 구체적인 예시를 들어 설명하는 편이 더 좋은 것 같습니다. 또한, 이후 부터는 "무작위 걸음"이라는 국문 번역보다는 그냥 "랜덤 워크"로 음역을 하도록 하겠습니다. 모든 사람이 그냥 "랜덤 워크"라고 하지 "무작위 걸음"이라고는 하지 않으니까요.
1차원 정수 격자 위에서의 랜덤 워크
가장 간단한 1차원 정수 공간에서의 랜덤 워크를 생각하겠습니다. 좁은 의미에서 랜덤 워크라고 하면 이 경우를 의미하고, 어쩌면 이 경우만을 랜덤 워크로 이해하고 계신분도 있을 것 같습니다. 1차원 랜덤 워크는 단순한데, 원점에서 시작하여 매 스텝 마다 +1 혹은 -1 만큼 움직이게 되는데 +1 만큼 움직일지 아니면 -1 만큼 움직일지는 각각 $\frac{1}{2}$ 의 확률로 주어지게 됩니다. 즉, $n$ 번째 스텝 이후의 위치를 $x_n$이라고 하고, 초기 위치를 $x_0 = 0$이라고 한다면, $[0,1]$ 범위에서 균등한 무작위 수 $r$에 대해서,
$$\begin{equation}
x_n=\begin{cases}
x_{n-1} + 1, &r \le \frac{1}{2} \\
x_{n-1} - 1, &r \gt \frac{1}{2} \\
\end{cases}
\end{equation}$$
의 점화식에 의해서 수열 $x_n$이 결정 됩니다. 랜덤 워크를 설명하는 확률 변수 $r$에 대해서 생각하는 대신에 "동전을 던진 후 앞/뒤가 나오면 +1/-1 만큼 움직인다"라고도 표현을 하는데, 실질적으로 같은 것 입니다.
수열의 점화식이 매우 간단하게 주어지는데, 한가지 문제는 이 과정에서 확률 변수 $r$이 도입된다는 것 입니다. 확률 변수 $r$에 의해서 앞으로 갈지 ($x_n = x_{n-1}+1$), 혹은 뒤로 갈지 ($x_n = x_{n-1}-1$) 가 결정되기 때문에, 보통 수학과정에서 배우는 결정론적인 점화식과는 약간 그 성격이 달라집니다. 결정론적으로 점화식이 주어진다면, $x_n$을 임의의 $n$에 대해서 바로 구할 수 있는데, 랜덤 워크와 같이 확률이 개입하게 된다면 그 때 그 때 $x_n$이 달라지기 때문에 이를 다루기 위해서는 추가적인 과정이 필요합니다.
랜덤 워크 실제 구현
우선, 위 점화식에 따라서 $x_n$하나를 만들어 보겠습니다. 이는 곳 $n$개의 확률 변수 $r_n$을 실제로 만드는 것과 동일합니다. 현실에서 확률이 $\frac{1}{2}$로 주어지는 확률 변수를 구현하고 싶다면, 동전을 던지거나 주사위를 던지면 됩니다. 그러나 이를 100번 1,000번 반복하는 것은 매우 귀찮은 일이니, 우리는 이 일을 컴퓨터에게 맡겨 보도록 하겠습니다. 아래는 파이썬을 이용하여 랜덤 위크를 구현한 것 입니다.
import numpy as np
import matplotlib.pyplot as plt
N = 100 ### 스텝 횟수
R = np.random.random(N) ### [0,1] 사이에서 균등 분포를 갖는 무작위 변수 N개 생성
X = []
x_0 = 0
X.append(x_0) ### X의 초기값 x_0 = 0으로 정의하고 수열에 포함
for n in range(1, N):
r = R[n]
x_prev = X[n-1]
if r <= 1/2:
x_next = x_prev + 1 ### 1/2<r 경우 +1
else:
x_next = x_prev - 1 ### 그렇지 않은 경우 -1
X.append(x_next)
plt.plot(range(N), X, marker = 'o', markersize=3, lw = 1)
plt.xlabel('n')
plt.ylabel('x_n')
plt.grid()
plt.show() ### 결과를 그래프로 출력위 프로그램을 실행하면 100 스텝을 거치는 동안 얻어진 $x_n$을 그래프로 그릴 수 있습니다. 예시는 아래와 같습니다.

확률 변수 $r$이 구체적으로 어떻게 구현되었느냐에 따라서 결과는 이와 다를 수 있습니다.

스텝을 1,000번 반복하면 위와 같은 결과를 얻을 수 있습니다.

1000스텝의 랜덤 위크를 10번 구현하여 하나의 그래프에 그린 예시 입니다. 서로 다른 색으로 그린 그래프는 각각 1000스텝 랜덤 워크를 의미하며, 확률 변수 $r$이 실제로 구현된 값에 따라서 랜덤 워크의 궤적이 달라지게 됩니다.
(위 그래프를 보면) 1000스텝을 걸었지만, 대부분의 경우 $x_{1000}$의 값은 $|x_{1000}| \lt 40$을 갖습니다. $x_{1000}$이 가질 수 있는 값의 범위는 $-1000 \le x_{1000} \le 1000$이지만, 한 번의 스텝에서 앞으로 갈 확률과 뒤로 갈 확률이 서로 같기 때문에 이를 한 번씩 반복하게 된다면 두 스텝을 걸었지만 제자리로 돌아오게 됩니다. 이와 같은 이유로 많은 걸음을 걷더라도 대부분의 경우 앞으로 간 만큼 뒤로 돌아오기 때문에 1000스텝을 걸어도 여전히 원점 근처에 위치하게 됩니다. 물론 위 그래프에서 맨 위에 보이는 파란색 그래프와 같이 멀리 $x_{1000} = 60$ 만큼 가게 되는 경우도 있습니다. 물론, 1000스텝을 걸었는데 60만큼 가는 것은 그리 많이 간 것은 아닌 것 같습니다.

이번에는 총 400개의 $x_n, n=1, 2, ..., 1000$ 수열을 생성하여 하나의 그래프로 그렸습니다. 각 수열을 옅은 회색으로 그렸는데, 진한 검은색으로 표현되는 것은 여러 그래프가 겹쳐졌기 때문입니다. 바로 앞 문단에서 설명한 것과 같이 대부분의 경우에는 1000걸음을 갔음에도 불구하고 $x_{1000}$값은 (플러스 마이너스) 50 범위에 위치합니다. 개중에는 +100까지 멀리간 경우도 있지만 그 경우는 희박합니다.
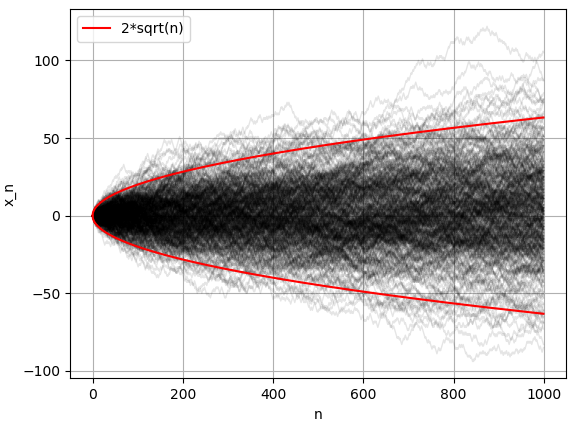
위 랜덤 워크 그래프에 $x_n = 2\sqrt{n}$를 붉은색으로 추가했습니다. 각 $n$에서 대부분의 그래프가 붉은색으로 표시한 영역안에 있고, 특히 진한 어두운색의 영역이 붉은색 그래프의 사이에 위치함을 볼 수 있습니다. (비록 구체적인 예시를 통해 추론하는 것 이니지만) 이를 통해서 랜덤 워크를 실제로 구현하면 대부분의 경우 "$|x_n| \lt 2 \sqrt{n}$이 된다" 라는 결론을 내릴 수 있습니다.
이항 분포를 통한 랜덤 워크의 설명
고등학교 수학 확률과 통계 시간에 "이항 분포"라는 것을 배웠습니다. 이항 분포는 "각각의 시행이 독립적이고 일어날 확률이 $p$로 주어졌을 때, 총 몇 번의 시행이 실현 되었나"를 기술하는 이산 확률 분포 입니다. 이항 분포의 정의(성질)을 잘 생각하면, 지금 우리가 다루고 있는 랜덤 워크와 아주 유사하다(같다)는 것을 확인할 수 있습니다.
총 $N$ 스텝이 랜덤 워크를 했을 때, +1의 스텝이 나온 횟수를 $N_+$라고 한다면, $N_+$는 정확하게 독립 시행의 확률이 $p = \frac{1}{2}$인 이항 분포와 동일합니다. -1의 스텝이 나온 횟수를 $N_-$라고 한다면, 당연히 $N = N_+ + N_-$가 되고, 이로 부터 $N_- = N - N_+$가 됩니다. $N$스텝을 걷고 나서 최종 $x_N$의 값은 $x_N = N_+ - N_- = 2N_+ -N$이 이 되는데, 여기서 $N$은 우리가 정해준 상수이고, $N_+$는 확률이 $p = \frac{1}{2}$인 이항 분포이기 때문에, $x_N$은 이항 분포의 성질에 따라서 $x_N$의 기대값과 분산(표준편차)를 구할 수 있습니다.
이항 분포 $B(N, p)$를 따르는 확률 변수 $X$의 평균과 표준 편차는 고등학교에서 배운 바와 같이
$$E(X) = Np$$
$$\sigma(X) = \sqrt{Np(1-p)}$$
입니다.
확률 변수 $X$에서 부터 유도된 또 다른 확률 변수 $Y = aX+b$가 있다고 했을 때, 확률 변수 $Y$의 평균과 표준편차는 역시 고등학교에서 배운 바와 같이
$$E(Y) = aE(X) = aNp$$
$$\sigma(Y) = a\sigma(X) = a\sqrt{Np(1-p)}$$
가 됩니다.
$N$ 스텝 랜덤 워크 이후의 위치 $x_N$은 확률 변수이고, 앞에서 본 바와 같이 $x_N = 2N_+ -N$이 됩니다. 여기서 $N_+$는 이항 분포 $B(N, \frac{1}{2})$를 따릅니다. 따라서 이로 부터,
$$E(x_N) = E(2N_+ - N) = 2E(N_+) - N = 2 (N \frac{1}{2}) - N = 0$$
$$\sigma(x_N) = \sigma(2N_+ - N) = 2 \sigma(N_+) = 2 (\sqrt{N \frac{1}{2} \frac{1}{2}}) = \sqrt{N}$$
이 됩니다. 요약하면 $x_N$의 평균은 0, $x_N$의 표준편차는 $\sqrt{N}$이 됩니다.
이항 분포를 배울 때, "이항 분포의 시행 횟수가 커지면 이항 분포는 정규분포와 닮아 간다"라는 것도 배웠을 것 입니다. 고등학교 수학에서는 이 성질을 이용하여 이항 분포에서 확률을 계산하기도 합니다. 이항 분포의 이 같은 성질을 이용하면 $x_N$의 분포 역시 정규 분포가 됨을 알 수 있는데, 위에서 구한 $E(x_N), \sigma(x_N)$를 활용하면,
"$x_N$은 평균이 0, 표준편차가 $\sqrt{N}$인 정규 분포다"
라고 결론 지을 수 있습니다.
실제로 위 결론이 성립하는지, 그렇지 않은지를 위에서 구현한 랜덤 워크 프로그램을 통해서 확인해보도록 하겠습니다.

위 그래프의 푸른색 히스토그램은 랜덤 워크 1000 번을 수행하여 얻은 1000개이 $x_{1000}$의 분포를 나타낸 그래프 입니다. 그리고 붉은색 선은 평균이 $0$, 표준편차가 $\sqrt{1000}$ 인 정규 분포를 그린 것 입니다. 삐죽삐죽한 모습이 나타나긴 하지만, 전체 걔형에서 실제 랜덤 워크의 결과와 정규 분포가 유사합니다.
랜덤 워크의 시행 횟수를 증가시키면 두 분포가 더욱 더 닮아감을 확인할 수 있는데, 랜덤 워크를 10,000회 반복하여 얻은 $x_{1000}$의 분포는 아래와 같습니다.
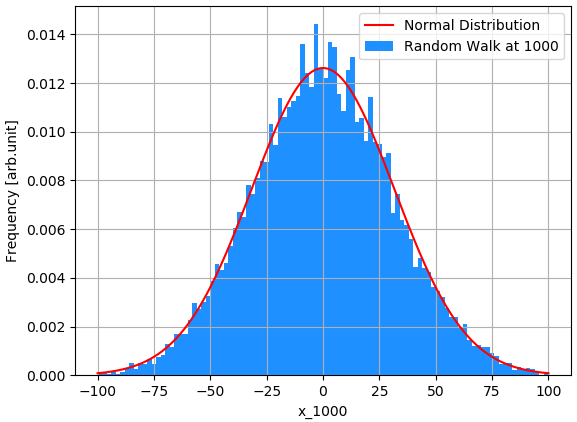
이 정도면 두 분포를 "같은" 분포라고 해도 될 것 같습니다. 어떤 분포가 정규 분포를 따른다면, 정규 분포의 성질에 따라서 확률 변수값이 $[-2\sigma, 2\sigma]$ 사이이 값을 가질 확률은 약 $95.5%$ 입니다. 따라서 위위위에 있는 회색으로 그려진 실제 랜덤 워크 구현 그래프에서 대부분의 검은색 그래프가 $2 \sqrt{n}$의 범위내에 있게 되는 것 입니다. 물론 $100% - 95.5% = 4.5%$의 그래프는 붉은색 영역 밖으로 빠져나가게 되지만, 정규 분포의 성질에 따라서 더 밖으로 빠져 나가게 될 확률은 급격하게 줄어들게 됩니다.
2차원에서 랜덤 워크
위에서는 1차원 정수 격자에서 랜덤 워크를 알아 보았습니다. 공간 차원을 하나 높여서 이제는 2차원 정수 격자에서의 랜덤 워크를 해보겠습니다. $n$번째 스텝에서 위치를 $(x_n, y_n)$과 같이 2차원에서 $(x,y)$ 죄표의 순서쌍을 이용하여 기술할 수 있습니다. $n+1$ 번째 위치$(x_{n+1}, y_{n+1})$ 에 대한 점화식을 정의해야 하는데,
$$\begin{equation}
(x_n, y_n)=\begin{cases}
(x_{n-1} + 1, y_{n-1}) & r \le \frac{1}{4} \\
(x_{n-1} - 1, y_{n-1}) & \frac{1}{4} \lt r \le \frac{1}{2} \\
(x_{n-1}, y_{n-1} + 1) & \frac{1}{2} \lt r \le \frac{3}{4} \\
(x_{n-1}, y_{n-1} - 1) & \frac{3}{4} \lt r\\
\end{cases}
\end{equation}$$
와 같이 정의할 수 있습니다. 각각 $\frac{1}{4}$의 확률로 좌($-x$방향), 우($+x$방향), 상($+y$방향), 하($-y$방향) 방향으로 한 칸(1만큼) 움직이는 것 입니다. 대각선 방향으로 움직이는 것을 추가해도 되지만, 편의상 단순히 한 칸만 움직이는 것으로 제한하겠습니다.
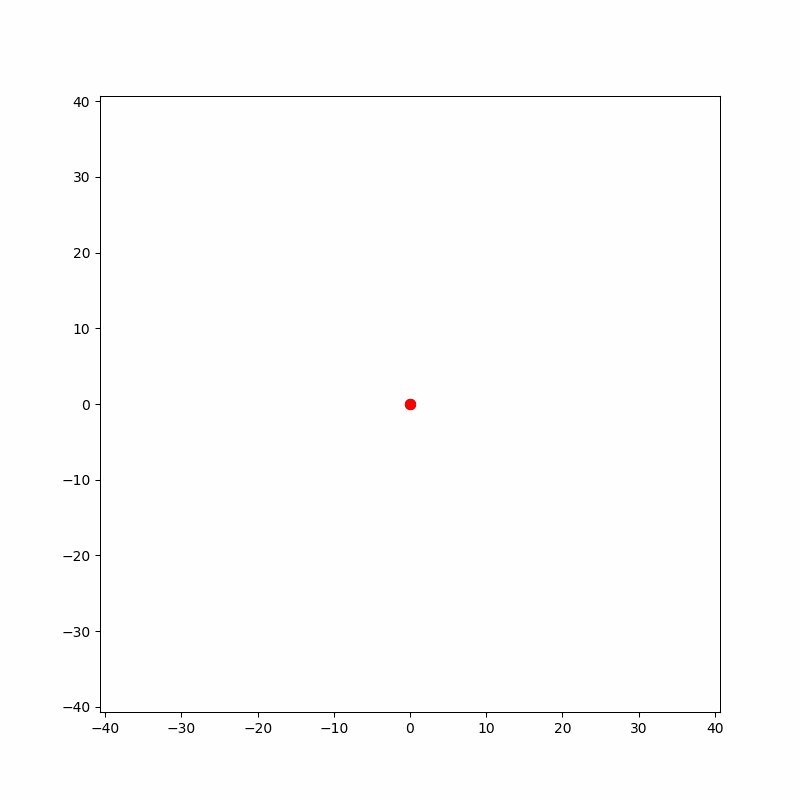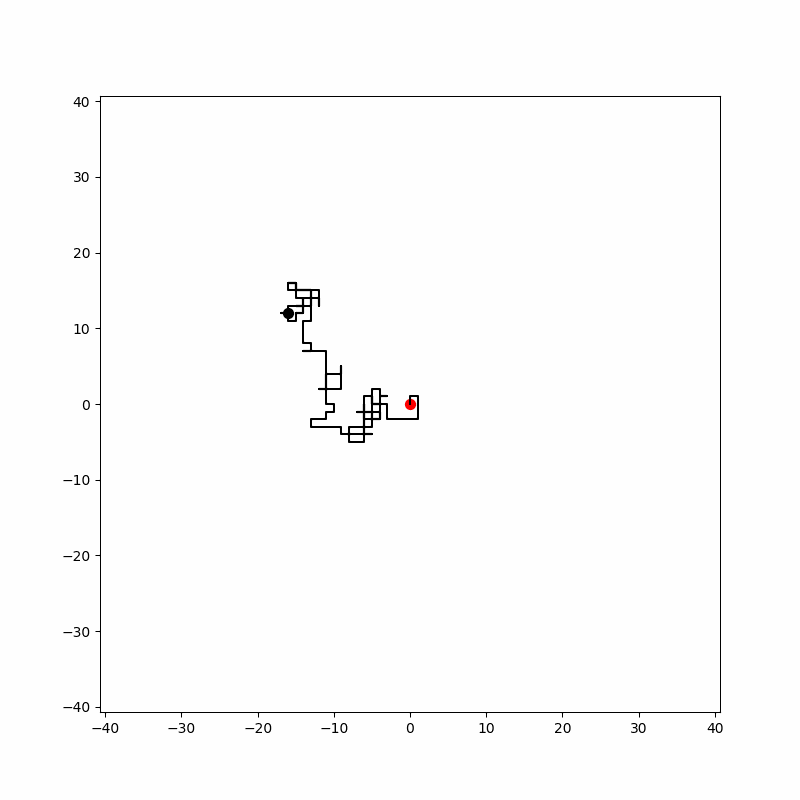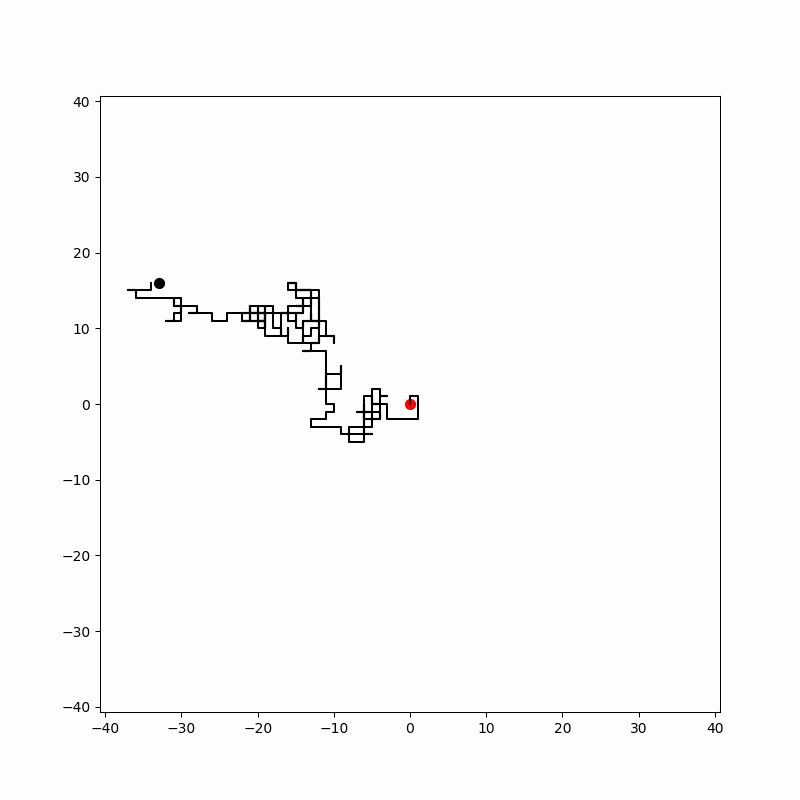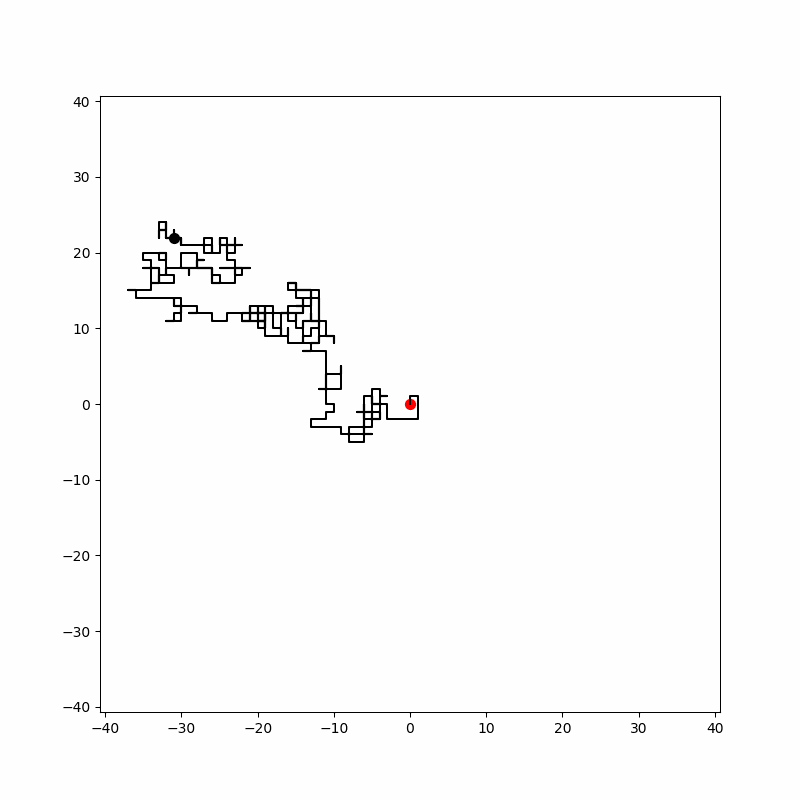
위 에니메이션은 2차원 랜덤 워크를 구현한 한 예시 입니다. 원점에서 출발하여 무작위 걸음을 하여 왼쪽 위로 움직입니다.
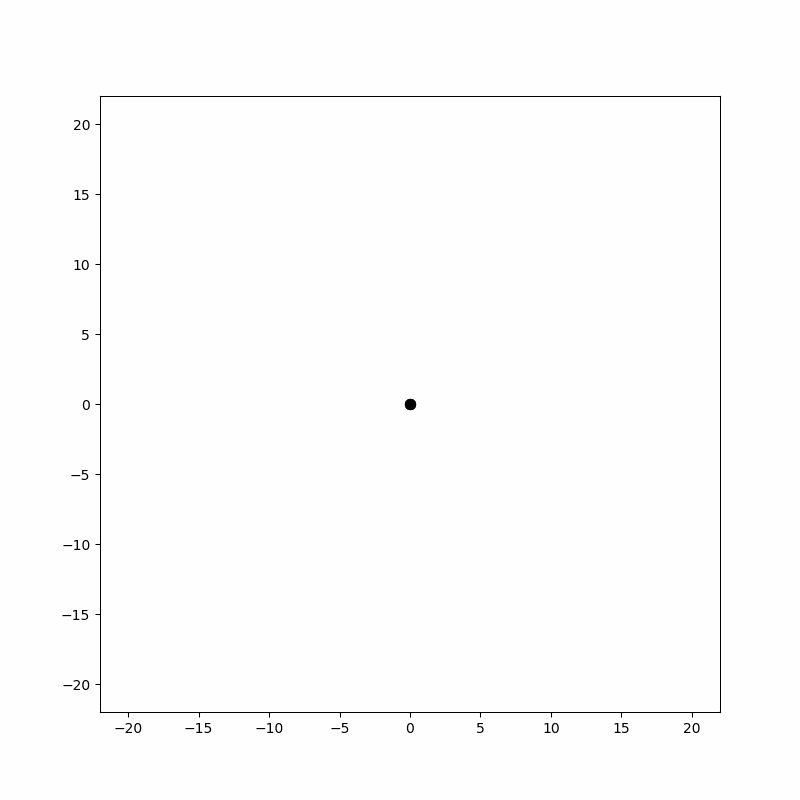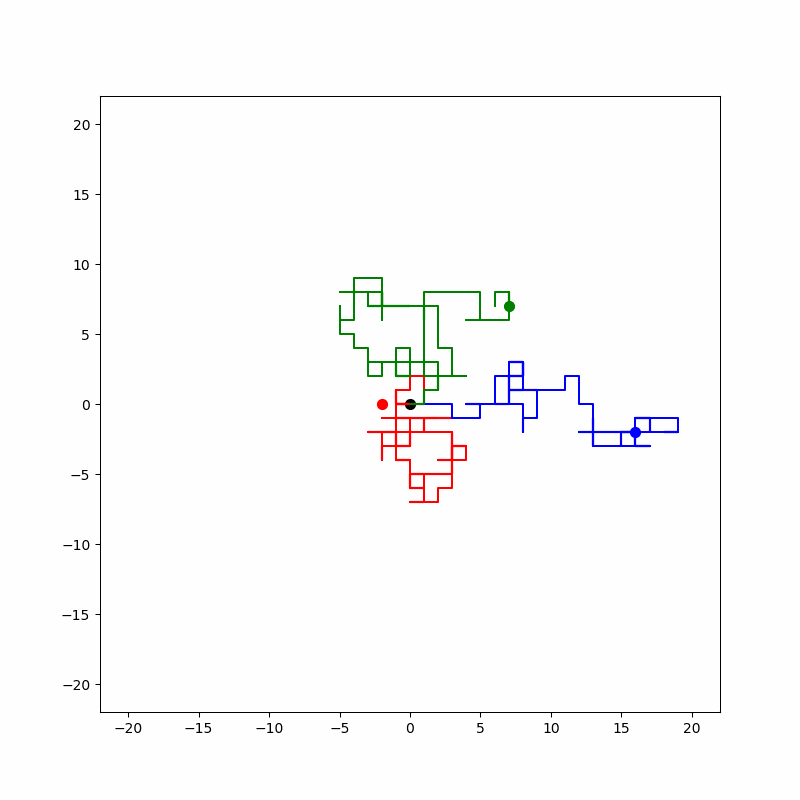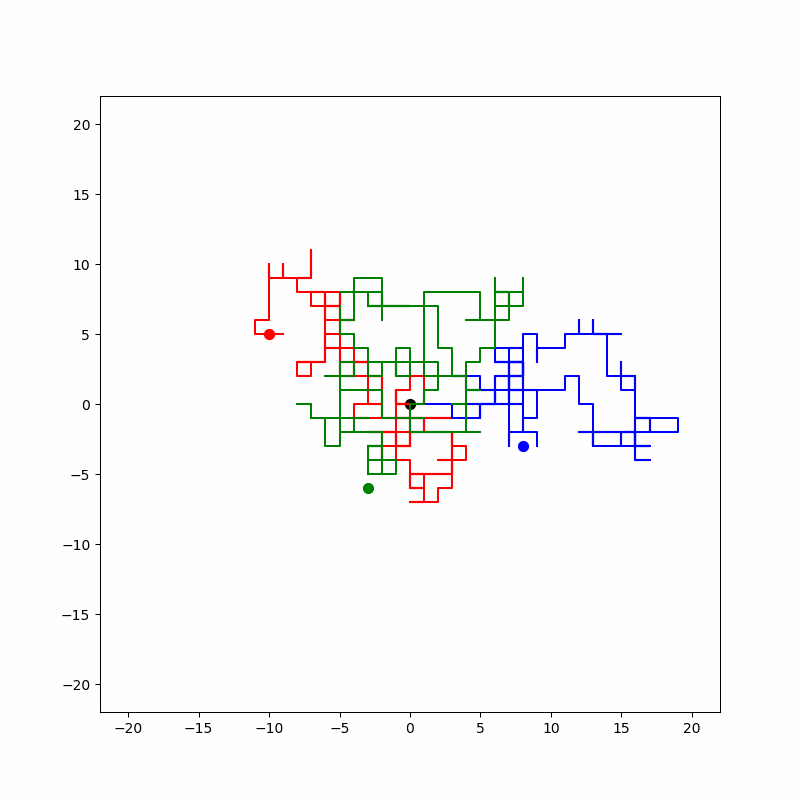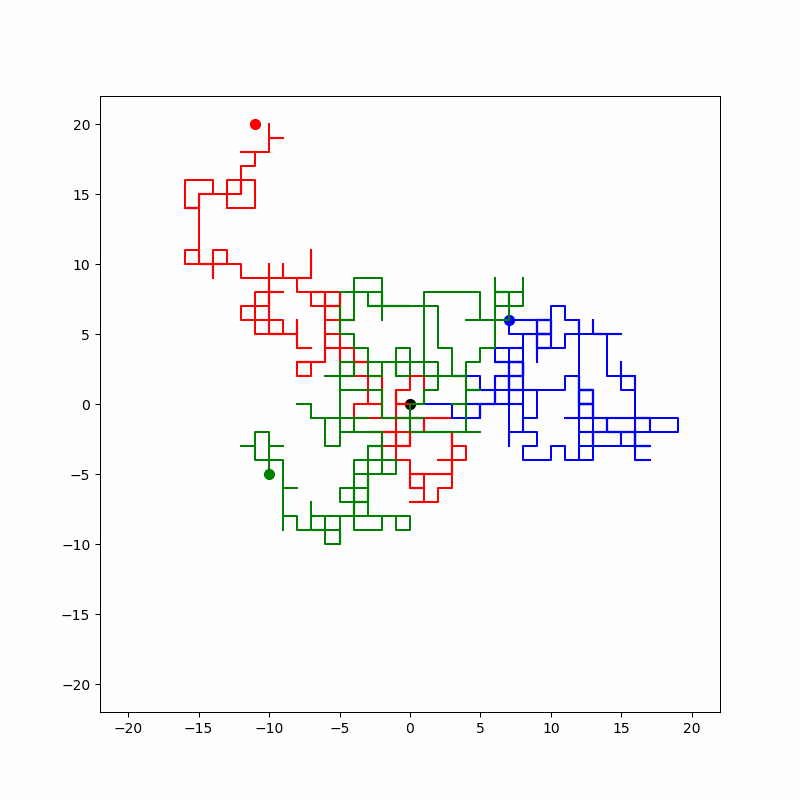
위 에니메이션은 동시에 3개이 랜덤 워크를 구현하였습니다. RGB의 경로가 생성됩니다.
2차원 랜덤 워크에서도 1차원 랜덤 워크에서 했던 것과 같은 방식의 분석이 가능합니다. 가장 중요한 결론 중에 하나는 역시나 $N$번째 스텝에서 $r_n = (x_n, y_n)$의 평균과 표준편차인데, 평균은 예상한것과 같이 $E(x_n) = 0, E(y_n) = 0$ 입니다. $x_n$의 경우 왼쪽/오른쪽으로 갈 확률이 같고, $y_n$의 경우 역시 위/아래로 갈 확률이 동일하기 때문입니다.
표준편차 역시 1차원에서와 같은 방법으로 구할 수 있는데, 약간 달라지는 것이 있습니다. 1차원에서 이동은 특정 공간 차원에서 이루어 지는 것이었지만, 2차원에서 이동은 두 공간 차원에서 일어나는 것이기 때문에, 특정 공간 차원의 위치 이동은 전체 스텝의 절반에만 해당된다는 것 입니다. 즉, 1000스텝을 움직이면 평균적으로 500 스텝의 이동은 $x$축 상에서 일어나고 나머지 500 스텝의 이동은 $y$측 상에서 일어납니다. 따라서 특정 공간 차원으로의 이동은 전체 스텝이 절반이 됩니다. 이를 1차원의 경우로 적용을 하면 $\sigma(x_N) = \sqrt{\frac{N}{2}}$가 됩니다. 1차원에서는 $\sqrt{N}$으로 주어졌는데, 바로 앞에서 설명한 바와 같이, 전체 이동에서 $x$축으로의 이동은 절반이기 때문에 $\frac{1}{2}$이 추가적으로 곱해지게 됩니다. $\sigma(y_N)$ 역시 같은 값을 갖게 됩니다.
$\sigma(r_N) = \sqrt{\langle r_N^2 \rangle}$를 계산할 수 있습니다. 이 값은 원점으로 부터의 거리의 표준편차입니다. 피타고라스 정리에 따라 $r_N^2 = x_N^2 + y_N^2$가 되고, 이미 앞에서 $\sigma(x_N), \sigma(y_N)$을 구했기 때문에, $\sigma(r_n) = \sqrt{N}$ 가 됨을 알 수 있습니다. 이 결과는 공간 차원이 3차원인 경우에도 일반화 하여 적용할 수 있습니다. 3차원인 경우에는 $\sigma(x_N) = \sigma(y_N) = \sigma(z_N) = \sqrt{\frac{N}{3}}$이 되고, $\sigma(r_N) = \sqrt{N}$이 됩니다. 특정한 방향으로만 생각한다면, 공간차원이 $D$ 라고 할 때, 표준편차가 $\frac{1}{\sqrt{D}}$와 같이 줄어듭니다. 이는 당연히 갈 수 있는 방향이 늘어나니, 특정한 방향으로 가게 되는 경우가 그에 비례하여 줄어들기 때문입니다.
https://www.youtube.com/shorts/wdDDzljAtSY
10개의 2차원 랜덤 워크가 만들어 내는 "그림" 입니다.
수학, 과학에서 랜덤 워크의 응용
랜덤 워크는 수학, 과학에서 매우 다양하게 활용 됩니다. 가장 유명한 예시 중 하나는 물리학에서 나오는 브라우니안 모션(Brownian motion)으로, 브라우니안 모션은 유체 속에서 떠 다니는 입자의 운동(궤적)을 설명하기 위한 이론으로 랜덤 워크를 이용하여 기술할 수 있습니다. 경제학에서는 "랜덤 워크 가설"을 통해 주식시장의 가격 변동을 예측하는데도 활용됩니다.
포스팅의 첫 문장에서 확률과정(stochastic process)라는 단어를 언급하였습니다. 확률과정은 확률변수(무작위변수)로 기술되는 "어떠한" 과정을 뜻 하는데, 지금까지 알아본 랜덤 워크는 확률과정의 대표적인 예시이지, 조금 더 강조하면 (적어도 개념적으로 볼 때) 랜덤 워크를 정확히 이해했다면, 확률과정을 이해했다고 볼 수 있을 만큼 랜덤 워크의 개념은 매우 중요합니다. 다음 포스팅을 통해서 랜덤 워크의 성질에 대해서 좀 더 알아 보고, 또한 이를 확장하여 일반적인 확률과정에 대해서도 알아 보도록 하겠습니다.
'수학' 카테고리의 다른 글
| 무작위 걸음(랜덤 워크 random walk) 103 : 주방정식(Master equation)을 이용한 시간에 따른 랜덤 워크의 확률 밀도 함수 계산 (0) | 2022.05.07 |
|---|---|
| 무작위 걸음(랜덤 워크 random walk) 102 : 앙상블 평균과 몬테 카를로 시뮬레이션 (1) | 2022.05.01 |
| 공간에 따라 굴절률이 달라지는 매질에서 빛의 경로의 일반화 : 측지선(geodesic)과 측지선 방정식(geodesic equation) (1) | 2022.04.23 |
| 159종의 띠부띠부씰을 다 모으려면 포켓몬빵 몇 개를 사야 할까? 쿠폰 콜렉터 문제 (4) | 2022.03.25 |
| 우도 함수(가능도 likelihood function)의 이해 (3) | 2021.12.27 |



