무작위 걸음(랜덤 워크 random walk) 102 : 앙상블 평균과 몬테 카를로 시뮬레이션

지난 포스팅 https://studyingrabbit.tistory.com/89

무작위 걸음(랜덤 워크 random walk) 101 : 파이썬 프로그램으로 구현

에서 랜덤 워크 (무작위 걸음)이 무엇이며, 랜덤 워크의 매우 기본적인 성질에 대해서 알아보았습니다. $D$차원 정수 격자 위에서 랜덤 워크는 현재 위치에서 임의의 축 방향으로 한 칸 만큼 이동할 수 있으며, 이동하는 방향은 확률적으로 주어졌습니다. 수 많은 랜덤 워크를 구현하여 $N$ 스텝 이후 위치 $x_N$의 분포를 구한다면, 이 분포는 이항 분포가 되며, $N$이 충분히 큰 경우에는 정규 분포로 근사할 수 있음을 확인했습니다. 이로 부터 $N$ 스텝 이후 원점(랜덤 워크를 시작한 지점)으로 부터의 거리의 표준편차는 $\sqrt{N}$으로 커진다는 것도 유도하였습니다. 

 

이번 포스팅에서는 약간 더 체계적인 방법으로 랜덤 워크를 바라보도록 하겠습니다. 여기서 말하는 "체계적인 방법"은 약간 더 수학적으로 엄밀하고, 일반화된 형태로 랜덤 워크와 관련된 값을 계산한다는 것 입니다. 그렇다고 해서 지난 포스팅에서 계산 방식이 "체계적이지 않았다"는 것은 아니지만, 이번 포스팅에서는 랜덤 워크만이 아닌 일반적인 확률 과정에서 사용될 수 있는 계산 방법을 다룰 것 입니다. 일반적인 확률 과정에서는 해석적인 방식으로 결과를 계산하는 것이 어렵습니다. 따라서 컴퓨터를 이용한 수치적인 방법을 도입할 수 밖에 없는데, 이를 위한 몬테 카를로 시뮬레이션의 방법을 알아 보도록 하겠습니다. 

 

확률 변수와 랜덤 워크의 경로

 

이전 포스팅에서 1차원 랜덤 워크의 점화식을 정의하면서 확률 변수 $r$를 도입하였습니다. $x_n$에서 $x_{n+1}$로 이동할 때, 확률 변수 $r$의 값의 크기에 따라서 $+1$이 될지, 아니면 $-1$이 될지 결정되었습니다. $0$번째 스텝에서 $n$번째 스텝으로 이동하기 위해서는 총 $n$개의 확률 변수 $r$이 필요합니다. 이를 $R_n = (r_1, r_2, ..., r_n)$으로 표현하도록 하겠습니다. 이 경우 $R_n$이 결정되면 $X_n = (x_1, x_2, ..., x_n)$이 완전히 결정 됩니다. 즉 하나의 $R_n$에 대해서 하나의 경로 $X_n$이 결정(대응) 됩니다. $x_n$이라고만 쓰면, $n$번째 스텝의 위치만을 뜻하기 때문에 $1$번째 스텝에서 $n$번째 스텝까지의 경로를 표현하기 위해서는 대문자 $X$를 써서 $X_n$으로 쓰도록 하겠습니다. 예를들면,

$$R_5 = (0.2, 0.4, 0.9, 0.1, 0.6)$$ 

에 대해서는 경로 

$$X_5 = (1, 2, 1, 2, 1)$$

가 대응 됩니다. 위에서 확률 변수 $r$를 $[0,1]$ 구간에서 균등 분포를 갖는다고 했는데, 사실 이는 조금 불편한 정의이며 $\{0, 1\}$ 의 값을 동일한 확률로 갖는다고 하는 것이 편합니다. 따라서 위에서 쓴 $R_5 = (0.2, 0.4, 0.9, 0.1, 0.6)$는 $(0, 0, 1, 0, 1)$ 로 쓰는 것이 더욱 편하며 $r = 0$이면 $x_{x+1} = x_n+1$, $r=1$이면 $x_{x+1} = x_n -1$ 이 됩니다. (지난 포스팅에서 확률 변수 $r$를 $[0, 1]$사이의 실수로 정의한 것은 파이썬 프로그래밍의 편의를 위한 것이었습니다.) 그래서 위 $R_5$와 $X_5$의 대응 관계를 다시 쓰면,

$$R_5 = (0, 0, 1, 0, 1) \Rightarrow X_5 = (1, 2, 1, 2, 1)$$

이 됩니다. 

 

앙상블 평균

 

단 한 번 랜덤 워크를 구현한다면, 수 많은 가능한 경로 중에서 단 하나의 경로가 선택 됩니다. 선택 된 경로는 확률 변수가 어떤 값을 갖느냐에 따라 결정되는데, 결정되는 방법은 바로 위 문단에서 알아 보았습니다. 만일 $N$ 스텝을 진행하는 랜덤 워크 경로 하나를 구현한다면, 확률 변수 $R_N = (r_1, r_2, ..., r_N)$가 필요합니다. 각 $r_i$는 0 혹은 1의 값을 갖기 때문에, 가능한 $R_N$의 가지수는 $2^N$개가 되고, 따라서 가능한 랜덤 워크의 경로 역시 $2^N$개가 됩니다. 이로 부터 $N$ 스텝 랜덤 워크의 가능한 모든 경로의 집합을 $S_N$ 라고 표현한다면, $S_N = \{X_N^1, X_N^2, ..., X_N^{2^N}\}$와 같이 표현할 수 있습니다. 여기서 윗 첨자는 제곱이 아니라 단순한 인덱스를 의미 합니다. $S_N$을 앙상블(ensemble)이라고 부릅니다. 앙상블이라는 용어는 주로 수학보다는 (수리)물리학에서 부르는 용어인데, 편의상 이 용어를 채택하도록 하겠습니다. 

 

한 번의 랜덤 워크를(가) 구현하면(실현되면), $S_N$ 중에서 하나의 원소 $X_N$가 선택됩니다. $X_N$의 선택은 확률적인 것이라 랜덤 워크를 구현할 때 마다 그 결과는 달라질 수 있습니다. 하지만 랜덤 워크의 구현을 여러번 한다면, 각 구현마다 선택되는 $X_N$은 $S_N$에서 동등한 확률로 선택되는 하나의 원소일 것이고, 만일 $2^N$ 번의 랜덤 워크를 구현한다면 $S_N$의 원소가 한 번씩 선택됨을 기대할 수 있습니다. 물론 이런 확률을 매우 희박하지만, 시행 횟수를 많이 늘린다면 $S_N$의 각 원소가 선택되는 횟수는 균등해질 것이라 기대할 수 있습니다. 

 

이 성질로 부터 "항상블 평균"을 구할 수 있습니다. 즉, 각 랜덤 워크의 시행에서 $S_N$의 원소 중 $X_N^i$가 선택될 확률을 $\frac{1}{n(S_N)}$ 으로 균등하다고 하고($n(S_N)$ = 집합 $S_N$의 원소의 갯수, 여기서는 $2^N$), 이 확률을 이용하여 필요한 값을 계산하는 것 입니다. 사실, 이런 방식은 이전 포스팅에서도 은연중에 도입하였는데, "앞으로 가는 스텝의 횟수 $N_+$"이 이항분포를 따른다는 성질로 부터 $x_N$의 평균, $x_N$의 표준편차를 계산하였습니다. 이 과정에 앙상블 평균이 녹아있습니다. 앙상블 평균의 형식을 이용하여 $x_N$의 평균을 표현하면,

$$\langle x_N \rangle = \sum_{X_N^i \in S_N} X_N^i(N)P(X_N^i)$$

이 됩니아. 여기서 $X_N^i(N)$은 $X_N^i$의 $N$ 번째 스텝의 값을 의미 합니다. $X_N^i = (x_1^i, x_2^i, ..., x_N^i)$ 이므로 $X_N^i(N) = x_N^i$가 됩니다. $P(X_N^i)$는 앙상블 $S_N$에서 $X_N^i$의 확률 입니다. $P(X_N^i) = \frac{1}{n(S_N)} = \frac{1}{2^N}$이고, $x_N = k$일 확률은 이항 분포의 성질에 따라 $P(x_N=k) = C(N, k) (\frac{1}{2})^k (\frac{1}{2})^{N-k}$가 됨을 이용하면 $\langle x_N \rangle = 0$ 이 됨을 (대칭성으로 부터)쉽게 보일 수 있습니다. 위 식에서 $C(N,k)$는 이항계수입니다. 

 

경로의 함수로 주어지는 임의의 값에 대해서 위와 같은 방식으로 앙상블 평균을 계산할 수 있습니다. 경로 $X^i_N$의 함수 $A = A(X^i_N)$이 있을 때, $A$의 앙상블 평균 $\langle A \rangle$은

$$\langle A \rangle = \frac{1}{n(S_N)} \sum_{i=1}^{n(S_N)} A(X^i_N) = \sum_{i=1}^{n(S_N)} A(X^i_N)P(X^i_N)$$

이 됩니다. 

 

확률 밀도 함수

 

이번에는 특정한 스텝 $n$에서 특정한 위치 $x$에서 입자를 발견할 확률을 앙상블 평균의 기법을 이용하여 계산해 보도록 하겠습니다. 이 값은 $n$ 스텝으로 구현될 수 있는 모든 경로 집합 $S_n$ 중에서 $n$ 스텝의 위치가 $x$인 경로의 갯수의 비율을 구하면 됩니다. 즉,

$$p(x, n) = \frac{1}{n(S_n)} \sum_{i=1}^{n(S_n)}\delta_{x, X^i_n(n)} = \sum_{i=1}^{n(S_n)} \delta_{x, X^i_n(n)} P(X^i_n)$$

입니다. 여기서 $\delta_{a,b}$는 

$$\begin{equation}
      \delta_{a,b}=\begin{cases}
        1,  & a=b \\
        0, & a \ne b
      \end{cases}
    \end{equation}$$

로 정의 됩니다. 위 정의를 간단히 표현하면 $p(x, n) = \langle \delta_{x, X_n(n)} \rangle$ 으로도 표현할 수 있습니다. 확률 밀도 함수값은 다른 어떤 값의 앙상블 평균 보다 중요한데, 그 이유는 경로 $X_N$에 의존하는 함수의 앙상블 평균은 확률 밀도 함수를 이용하여 구할 수 있기 때문입니다. 예를 들어, 앞에서 구했던 $\langle x_n \rangle$ 값은

$$\langle x_n \rangle = \sum_{k=-\infty}^{\infty} x_k p(x_k, n)$$

와 같습니다. 위에서 정의한 $\langle x_n \rangle$이 정의와 확률 밀도 함수의 정의를 잘 비교해 보면 $\langle x_n \rangle$을 확률 밀도 함수를 이용하여 위와 같이 구할 수 있음을 쉽게 확인할 수 있을 것 입니다. 확률 밀도 함수를 이용하여 임의의 함수의 앙상블 평균을 계산하는 것은 이미 고등학교 시절 확률과 통계 과목에서 부터 배워온 것이라 생각하여 추가적인 설명은 생략합니다.

 

확률 밀도 함수의 주방정식(master equation)

 

주방정식(master equation)은 $n+1$ 번째 스텝의 확률 밀도 함수 $p(x, n+1)$를 그 보다 한 스텝 앞선 $n$ 번째 스텝의 확률 밀도 함수 $p(x, n)$를 이용하여 표현하는 방정식을 가리킵니다. 1차원 정수 격자 공간에서 정의된 랜덤 워크의 확률 밀도 함수의 주방정식은 

$$p(x, n+1) = \frac{1}{2} p(x-1, n) + \frac{1}{2} p(x+1, n)$$

이 됩니다. 특별한 설명을 하지 않더라도 직관적으로 위와 같은 식이 성립해야 함을 알 수 있는데, $n+1$ 번째 스텝에서 위치 $x$에 위치할 수 있으려면 $n$ 번째 스텝에서 $x-1$ 혹은 $x+1$에 있어야 합니다. $n$ 번째 스텝에서 $x-1$에 있던 입자(랜덤 워커)는 $n+1$ 번째 스텝에서 절반의 확률로는 $x$로 옮겨지게 되고, 다른 절반의 확률로는 $x-2$의 위치로 옮겨가게 됩니다. 따라서 $x-1$의 확률 밀도 함수의 절반이 그 다음 스텝에서 $x$의 확률 밀도 함수로 기여하게 됩니다. $n$ 번째 스텝에서 $x+1$의 위치에 있던 입자(랜덤 워커)에 대해서도 동일하게 적용 될 수 있습니다. 초기 상태의 확률 밀도 함수 $p(x, 0)$과 주방정식만 있다면, 임의의 스텝과 위치에서의 확률 밀도 함수를 계산할 수 있습니다. 

 

몬테 카를로 시뮬레이션

 

앙상블 평균을 계산하기 위해서는 집합 $S_N$의 모든 원소 $X_N^i$에 대한 정보가 필요합니다. 1차원 정수 격자 랜덤 워크에서는 $X_N^i$가 매우 간단하게 주어지기 때문에, 해석적인 방법으로 $X_N^i$에 대한 정보를 쓸 수 있지만, 일반적인 확률 과정이나 (아직은 도입하지 않았지만) "일반화된 랜덤 워크" 과정에서 해석적인 계산은 불가능합니다. 이를 위해서 컴퓨터를 이용한 수치해법을 쓸 수 밖에 없습니다. 

 

안타깝게도 컴퓨터를 이용한다고 하더라도 모든 문제가 해결되는 아닙니다. 1차원 정수 격자 랜덤 워크 $N$ 스텝 경로의 앙상블 평균을 구하려고 한다면, 원칙적으로는 $2^N$개에 해당하는 모든 경로 $S_N$을 구하고, 이로 부터 앙상블 평균 값을 구해야 합니다. $N$이 작다면 $2^N$개의 모든 구체적인 $X_N$을 구하고, 이를 이용하여 무언가를 계산할 수 있지만, $N$이 무척 커진다면 이 방법은 불가능 합니다. 예를 들어, $N=1,000$이라고 한다면 $S_N$의 원소는 총 $2^{1000} \approx 10^{301}$ 이라는 어마무시한 큰 숫자가 됩니다. $10^{301}$개나 되는 모든 경로 $X_N^i$를 계산하거나 저장할 컴퓨터 하드웨어는 충분하지 않습니다. 

 

이 같은 문제를 피하기 위해서 몬테 카를로 방법을 택할 수 있습니다. 이전 포스팅 https://studyingrabbit.tistory.com/33?category=911605 

몬테 카를로 시뮬레이션(Monte Carlo Simulation) 의 이해 : 원주율값 구하기 (+파이썬 시뮬레이션 코드)

에서 몬테 카를로 시뮬레이션과 이를 이용한 적분 방식을 설명한 적이 있습니다. 이 포스팅에서 설명한 방식을 앙상블 평균을 계산하는데도 적용할 수 있습니다. 어쩌면, 몬테 카를로 방법을 이용하여 적분을 하는 것 보다, 몬테 카를로 방법을 이용하여 앙상블 평균을 계산하는 것이, 몬테 카를로 방법을 보다 직관적이고 직접적으로 이용하는 것이라 할 수 있습니다. 아니, 좀 더 과장하면 몬테 카를로 기법은 앙상블 평균을 계산하기 위해 도입된 방법이라고 할 수도 있습니다. 

 

몬테 카를로 기법을 이용하여 앙상블 평균을 구할 때는 $2^N$개에 해당하는 $S_N$ 집합의 원소 중에서 몇몇개의 원소를 직접 생성하고 생성된 원소들을 이용하여 평균을 계산합니다. "몇몇개" 라고 표현한 것을 $M$개라고 한다면, 실제 $2^N$개의 원소(경로) 중에서 $M$개를 뽑고, 이 $M$개가 전체 집합인양 계산하는 것 입니다. 몬테 카를로 계산 과정에서 특정 원소가 선택 되는 확률이 $S_N$의 집합에서 특정 원소의 확률과 동일하다면, $2^N$개의 원소를 한 번씩 모두 선택하지 않더라도, 이 보다 더 적은 수의 $M$개만 뽑아서 평균을 취한 것이 앙상블 평균의 값과 유사할 것이라는 가정이 깔려 있습니다. 

 

몬테 카를로 시뮬레이션을 앙상블 평균 계산

 

$D$차원 정수 격자 랜덤 워크의 많은 문제는 해석적인 방법으로 풀 수 있지만, 잠시 동안은 해석적인 방법으로 푸는 것이 불가능하다고 가정하겠습니다. 혹은 일반화된 랜덤 워크를 풀기 위해서 몬테 카를로 시뮬레이션을 구현하는데, 우리의 프로그램이 제대로 작성돼 있는지 확인하기 위해서 해석적인 해를 알고 있는 $D$차원 정수 격자 랜덤 워크를 통해 테스트 한다고 생각해도 됩니다. 어쨌든, 우리는 매우 일반적인 경우의 확률 과정의 문제를 푸는 것이 최종 목표이기 때문에, 해석적인 일반해는 얻을 수 없다고 가정하는 것이 옳습니다. 

 

2차원 공간 정수 격자 공간에서 랜덤 워크를 생각하겠습니다. 앞에서 1차원 공간에서는 {앞, 뒤}의 가능성이 있고, 이에 대응하는 확률 변수는 $\{0, 1\}$ 값을 가지면 충분했습니다. 2차원 공간에서는 상,하,좌,우의 움직임이 가능하기 때문에 이에 대응되는 확률 변수는 $\{0, 1, 2, 3\}$의 값을 가져야하고, 따라서 $N$ 스텝 랜덤 워크의 경우 총 가능한 경로의 갯수는 $4^N$개가 됩니다. 이 점을 유념하고, $N = 500$ 스텝 랜덤 워크 $100$개를 구현해 보도록 하겠습니다. 파이썬 시뮬레이션으로 구한 결과는 아래와 같습니다. 

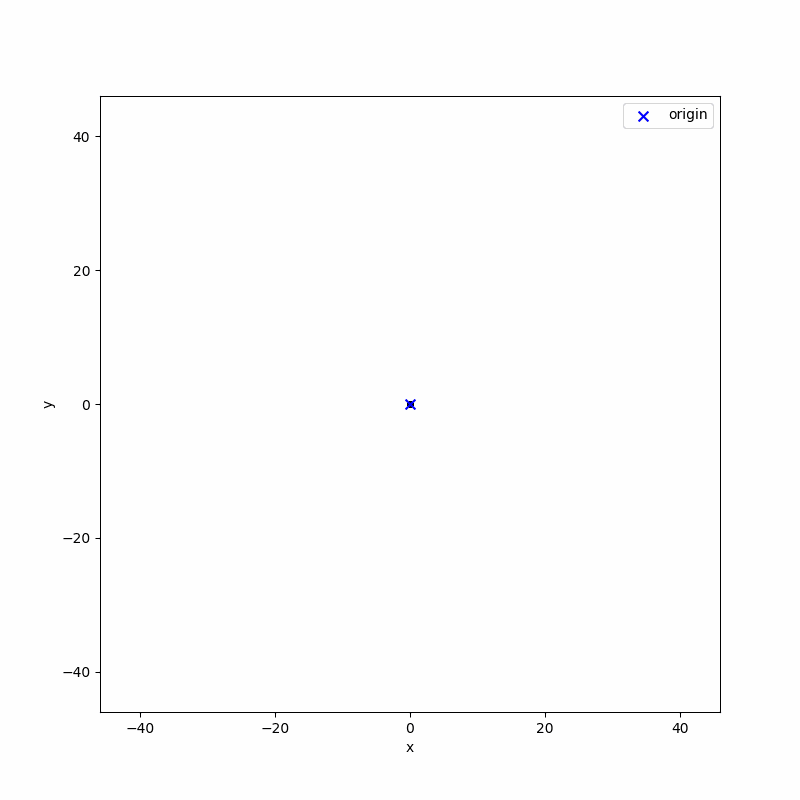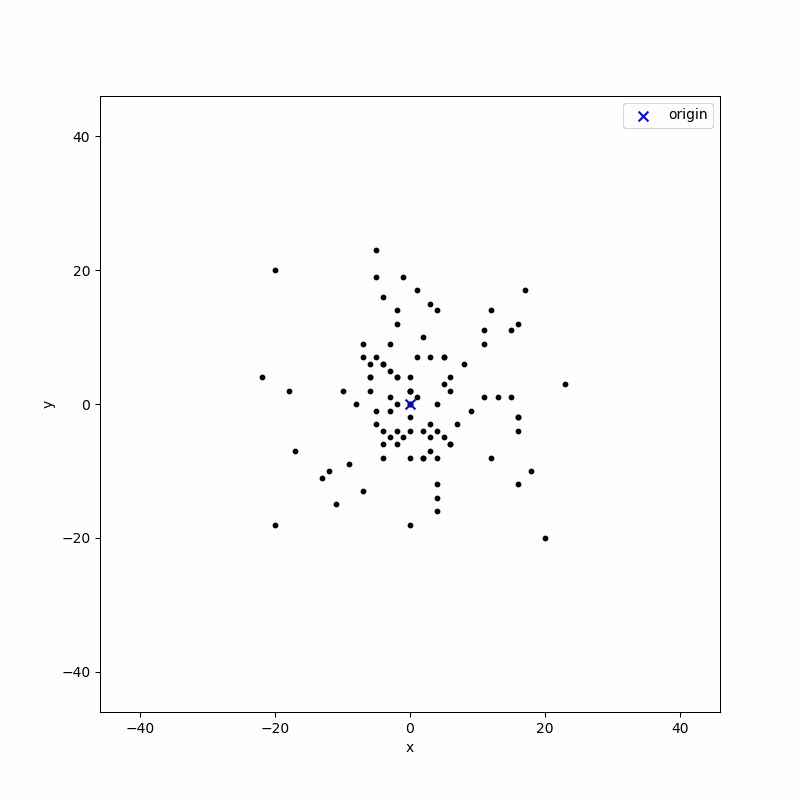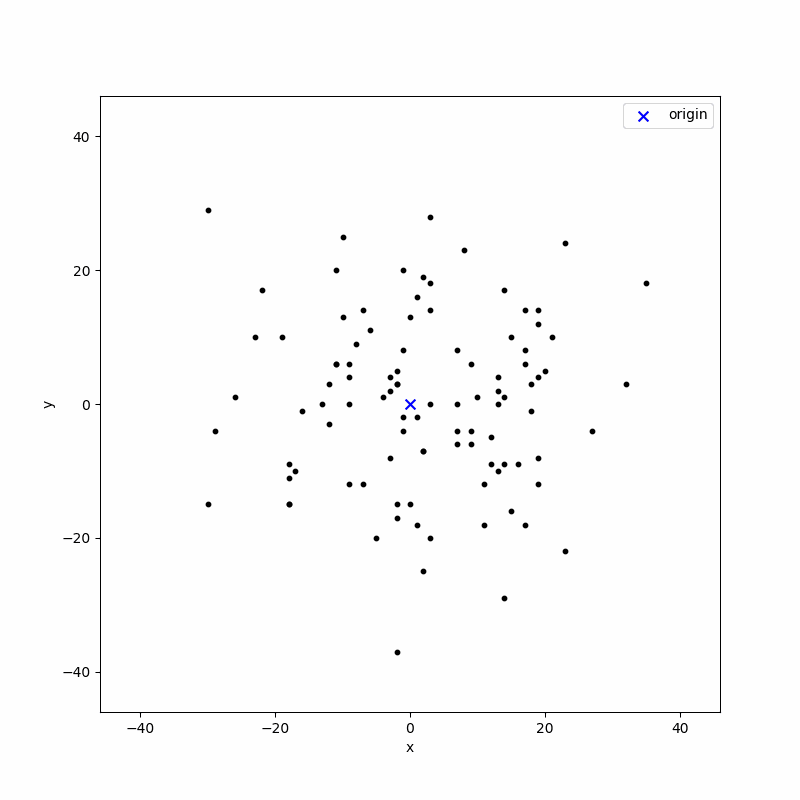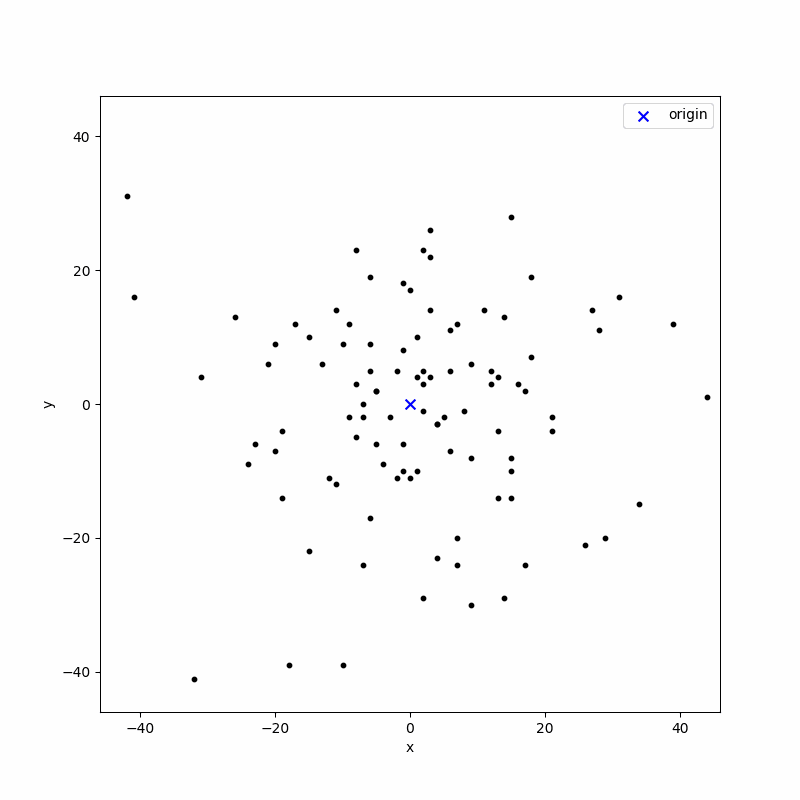
위 에니메이션에서 푸른색 X 표시는 원점을 나타냅니다. 각 랜덤 워크는 원점에서 시작하여 각자의 경로에 따라 움직입니다. $N = 500$스텝, $M = 100$ 개에 대한 랜덤 워크의 경로 $X_N^{i}, i= 1, 2, 3, ..., M$에 대한 정보를 모두 갖고 있기 때문에, 이를 이용하여 앙상블 평균(의 몬테 카를로 시뮬레이션 근사값)을 계산할 수 있습니다. 

 

$\langle x_n \rangle$, $\langle y_n \rangle$, $\langle r_n^2 \rangle$ 을 구해 보도록 하겠습니다. 앙상블 평균과 몬테 카를로 시뮬레이션(근사)의 정의에 따라서,

$$\langle x_n \rangle = \frac{1}{M} \sum_{i=1}^{M} X_N^i(n)_x, \langle y_n \rangle = \frac{1}{M} \sum_{i=1}^{M} X_N^i(n)_y$$

입니다. 여기서 $X_N^i(n)_x$는 $i$번째 랜덤 워크 경로의 $n$ 스텝의 위치의 $x$ 성분입니다. 또한, 

$$\langle r_n^2 \rangle = \langle x_n^2 + y_n^2 \rangle = \frac{1}{M} \sum_{i=1}^{M} X_N^i(n)_x^2 + X_N^i(n)_y^2$$

를 계산하면 됩니다. 

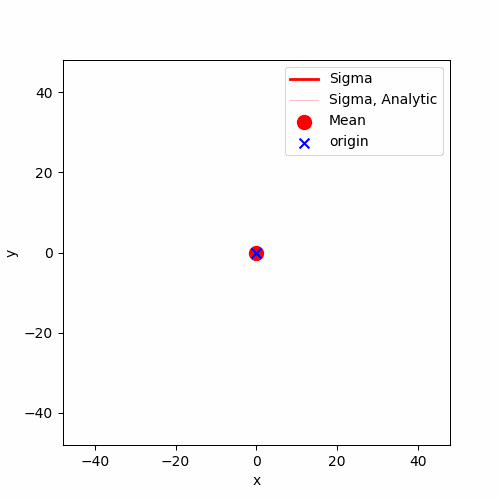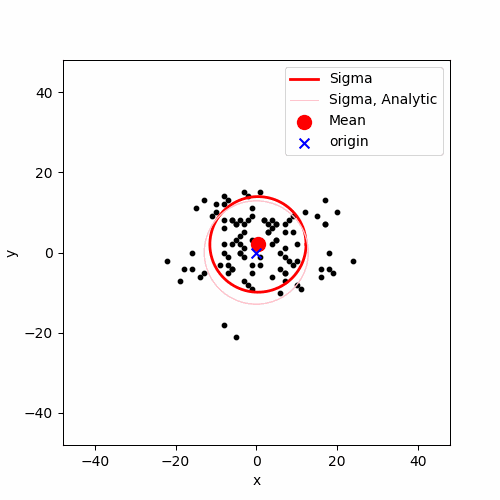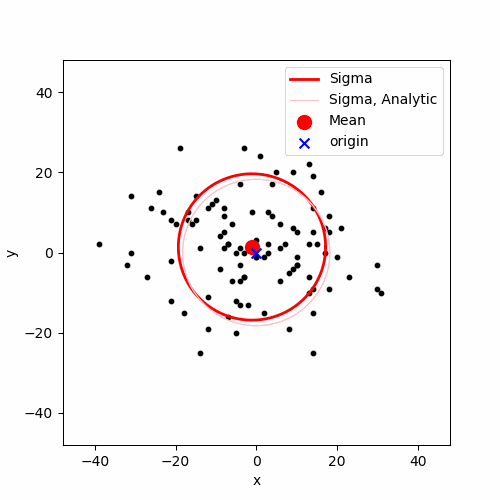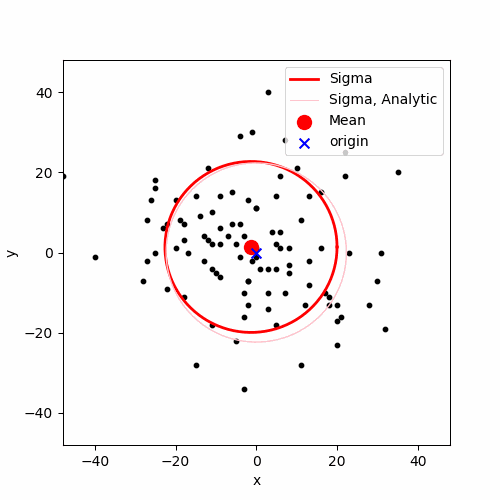
에니메이션에 $\langle r_n \rangle$과 $\sqrt{\langle r_n^2 \rangle}$ 를 함께 표현하면 위와 같습니다.  $\langle r_n \rangle$는 붉은색 큰 점으로 표시하였고, 이 붉은색 큰 점 중심으로 하고 반지름이 $\sqrt{\langle r_n^2 \rangle}$인 원을 붉은색 실선으로 표시하였습니다. 분홍색 얇은 실선이 보이는데, 이는 해석적으로 부터 얻은 $\sqrt{\langle r_n^2 \rangle}$의 값인 $\sqrt{n}$입니다. 해석적인 값과 실제 몬테 카를로 시뮬레이션으로 랜덤 워크를 구현하여 계산한 값이 정확하게 일치하지는 않지만(평균값인 붉은색 큰 점이 원점을 벗어나 있거나, 붉은색 실선 원과 분홍색 실선 원이 약간 빗겨난다거나), 전체적인 경향에서 해석적인 값과 몬테 카를로 시뮬레이션의 결과가 유사합니다. 위 시뮬레이션에서는 총 $M = 100$개의 랜덤 워크를 구현하고 이를 통해서 평균을 계산했는데, 만일 $M$ 값을 더 크게 한다면 해석적인결과과 몬테 카를로 계산의 결과가 더 유사할 것 입니다. ($M = 1000$ 계산의 결과를 첨부하고 싶은데, 티스토리 이미지 업로드 용량 제한이 20MB라 못합니다) 

 

위 두 에니메이션에서는 각 래덤 워크의 위치를 검은색 점으로 표시하였는데, 표현 방법을 약간 바꾸어 그림을 그릴 수 도 있습니다. 위치를 점으로 표현하는 것이 아니라 평활화(smoothing)을 하여서 하나의 점을 "많은 데이터"처럼 그리는 것 입니다. 이 방법은 불연속적인 데이터를 연속적인 데이터처럼 변환하는 것이라고 생각해도 됩니다. 이렇게 하여 표현하면,

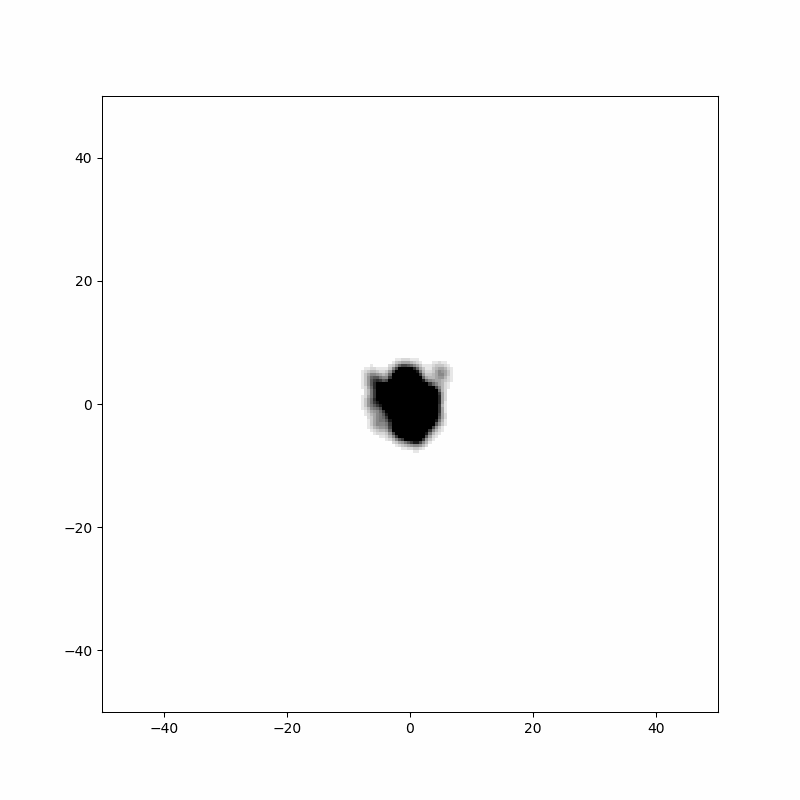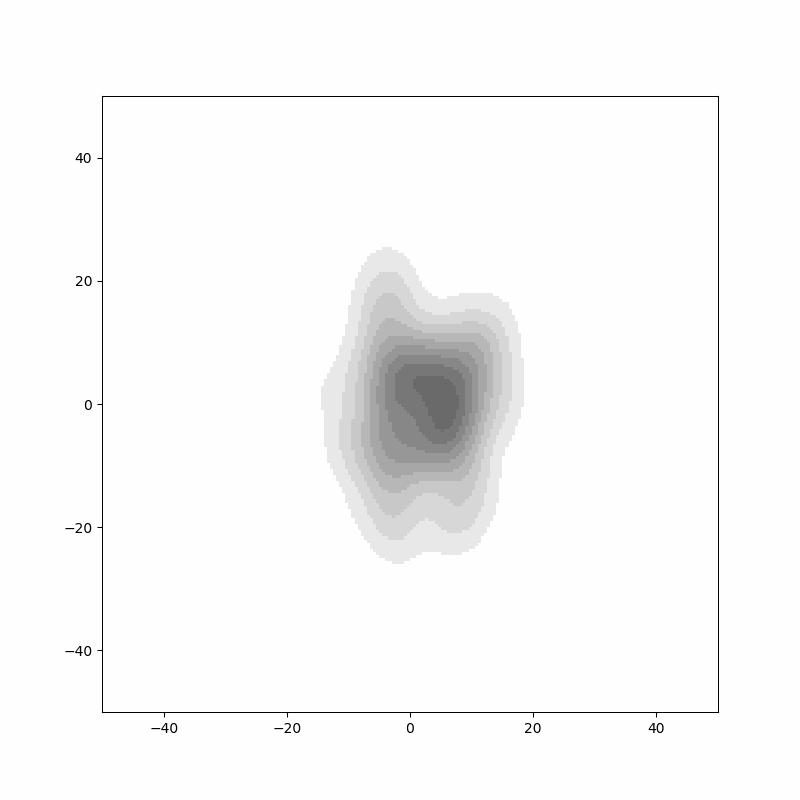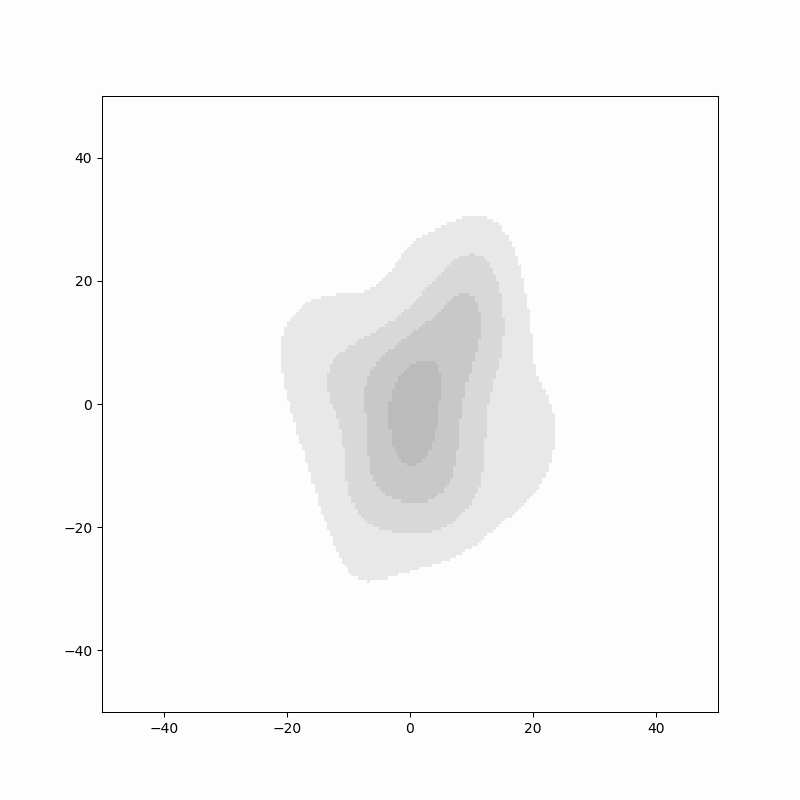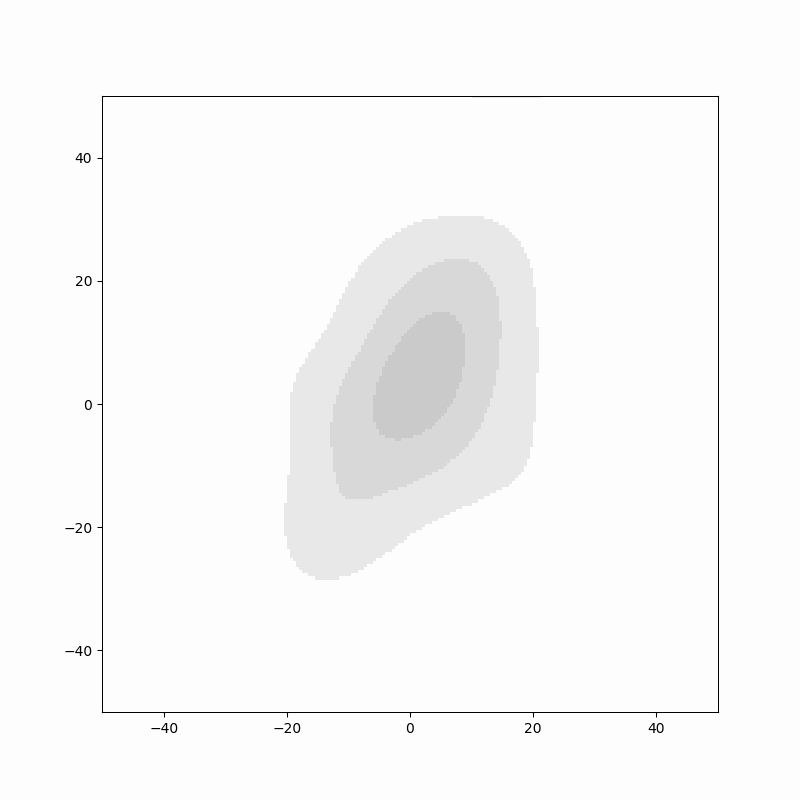
결과는 위와 같습니다. 임의의 스텝 $n$에서 랜덤 워크 경로가 많은 곳은 진한색으로, 적은 곳은 한색으로 그 밀도를 표현하였습니다. 등고선처럼 표시가 되니 분포의 변화를 짐작할 수 있습니다. 랜덤 워크는 원점엠서 시작하기 때문에 $n$값이 작을 때는 원점 주변만 진한색(밀도가 높은 영억)으로 표시되고, 스텝이 진행될 수 록 경로의 위치는 $\sqrt{n}$에 비례해서 원점에서 멀어지기 때문에 회색의 값은 점점 더 원점에서 멀어지게 됩니다. 랜덤 워크가 미칠 수 있는 범위는 넓어지지만 반대로 밀도는 낮아지기 때문에 밀도를 표시하는 색은 점점 더 옅어지게 됩니다. 

 

치우친 랜덤 워크 (Biased random walk)

 

지금까지는 다음 스텝으로 움직임이 동등한 확률인 경우만을 다루었습니다. 1차원 정수 격자 랜덤 워크에서는 +1, -1은 각각 50%:50%인 경우를, 2차원 정수 격자 랜덤 워크에서는 +x축, -x축, +y축, -y축으로 움직일 확률이 각각 25%:25%:25%:25%인 경우를 다루었습니다. 이번에는 이 조건을 일반화 해 보겠습니다. 즉, 1차원에서는 +1의 확률을 $p$, -1의 확률을 $1-p$로 놓는 것 입니다. 일반적으로 $p \ne 0.5$ 입니다. 

 

만일 $p = 0.6$과 같이 +1 로 이동할 확률을 높게 둔다면, 랜덤 워크의 스텝의 기대값 $\langle x_n \rangle$은 양수가 될 것 입니다. 이항 분포의 성질을 이용하여 $\langle x_n \rangle$과 $\langle x_n^2 \rangle$을 각각 해석적인 방법으로 구할 수 있는데, 이번 포스팅에서는 보다 일반적인 확률 과정의 문제를 푸는 것을 목적으로 하기 때문에, 이 문제를 몬테 카를로 방법을 통해서 알아 보도록 하겠습니다. 시뮬레이션 코드에서 각 방향으로 진행할 확률을 동등하지 않게 바꾸기만 하면 됩니다. 

 

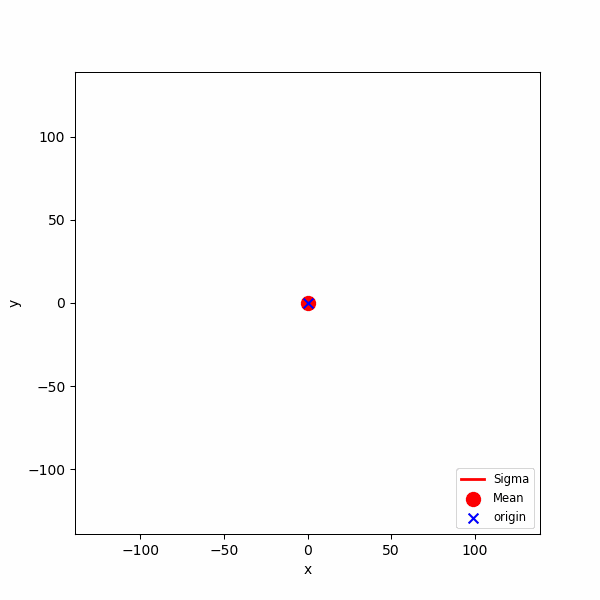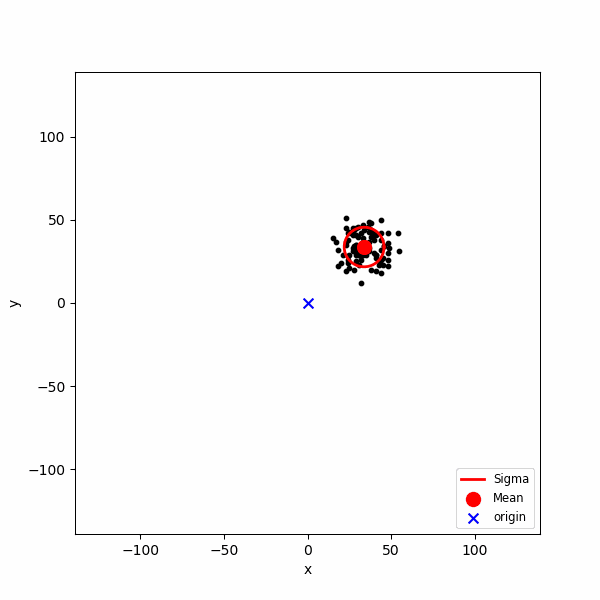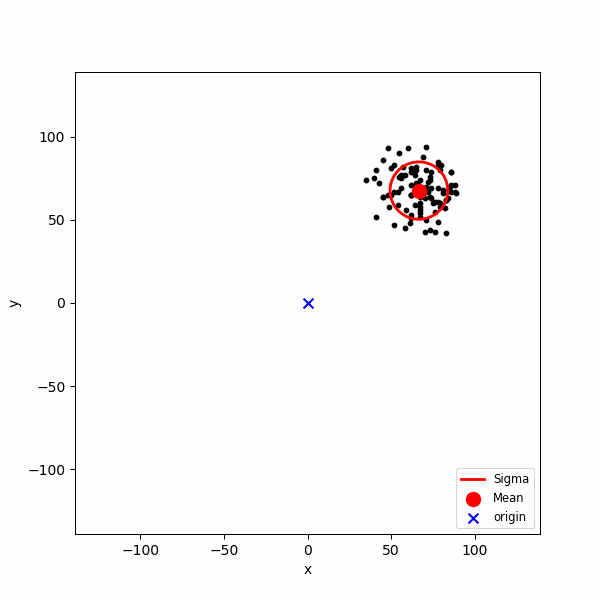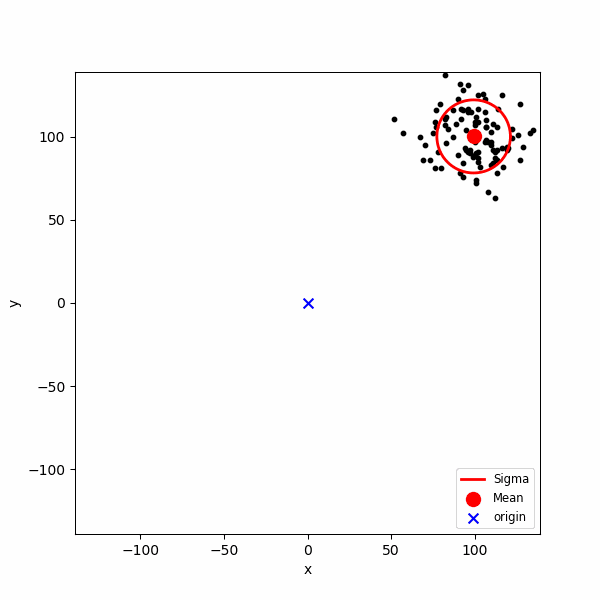
$(+1, 0), (-1, 0), (0, +1), (0, -1)$ 방향으로의 스텝의 확률을 $(0.35, 0.15, 0.35, 0.15)$로 정의한 2차원 정수 격자 공간에서의 랜덤 워크 결과 입니다. $N = 500$ 스텝의 경로 $M = 100$개를 생성하였습니다. 앞의 에니메이션에서와 같이 각 $n$에서 경로의 평균과 표준편차를 계산하여 보기 쉽게 표현하였습니다. 위 각 스텝의 확률에서 볼 수 있듯, 랜덤 워크의 경로는 스텝이 증가함에 따라서 전체적으로 오른쪽 위 방향을 향합니다. 이는 당연한데 $(+1, 0)$의 확률이 $(-1,0)$의 확률 보다 높기 때문에 평균적으로 $(+1, 0)$방향으로 움직일 거라 예상할 수 있고, $y$축 역시 동일하게 $(0, +1)$의 확률이 $(0, -1)$의 확률 보다 높기 때문에 평균적으로 $(0, +1)$방향으로 움직일 거라 예상할 수 있습니다. 개별 랜덤 워크의 경로는 말 그대로 "랜덤" 하지만, 전체적으로는 우상향 항는 경향을 보입니다. 이와 같이 경로의 평균이 특정 방향으로 움직이는 랜덤 워크를 "치우쳐진 랜덤 워크" 라고 합니다. 

 

랜덤 워크를 (일반인에게) 소개하는 글에서 주로 랜덤 워크를 "술취한 사람이 몸을 가누지 못해 좌우로 움직이면서 걸어가는 것"으로 표현하는데, 치우쳐진 랜덤 워크는 "오르막 혹은 내리막이 있는 길에서" 술취한 사람이 몸을 가누지 못해 좌우로 움직이면서 걸어 가는 것이라고 수식어를 추가할 수 있습니다. 술취한 사람은 좌우로 비틀 거리면서 걸어가겠지만, 전체적으로 움직이는 경향은 내리막을 향해 걸을것 입니다. 물론 중간 중간에 오르막 방향을 향해 걷긴 하겠지만, 확률적으로 내리막 쪽을 발을 디딜 가능성이 높습니다. 

 

랜덤 워크와 확산 방정식

 

위 에니메이션을 보면, 이는 마치 물에 떨어진 검은색 잉크 방울이 점점 주변으로 퍼저 나가는 것과 비슷합니다. 혹은 원점에서 시작한 연기가 시간에 따라서 주변으로 퍼져 자가는 것으로도 볼 수 있습니다. 물에서 잉크 방울이 퍼저나가는 것이나 공기 중에서 연기가 퍼저 나가는 현상은 모두 랜덤 워크로 기술 할 수 있습니다. 물 속에서 잉크 입자나 공기 중에서 연기 입자가 움직니는 것은 랜덤 워크와 닮아 있기 때문입니다. (우리가 다룬) 랜덤 워크에서는 공간은 격자 단위로 불연속적이고, 시간 역시 스텝의 단위로 불연속적 입니다. 불연속적인 시간과 공간을 일반화하여 연속적인 시간과 공간 단위에서 랜덤 워크를 구현한다면 이는 곧 확산 방정식과 동치가 됩니다. 다음 포스팅에서는 랜덤 워크의 시간과 공간을 연속화하여 확산 방정식을 유도해 보겠습니다.