지난 포스팅 복습
지난 세 번의 포스팅에서 랜덤 워크에 대해서, 그리고 컴퓨터 시뮬레이션을 통해서 랜덤 워크를 어떻게 연구 할 수 있는지을 알아 보았습니다. 이번 포스팅에서는 약간 다른 방식으로 랜덤 워크를 이해할 것인데, 이전 포스팅에서 가정한 "스텝"의 불연속한 성질을 연속적으로 바꿔 볼 생각입니다. 또한 "유한"을 "무한"으로 바꿔 볼 생각입니다. 이를 통해서 랜덤 워크로 부터 확산 방정식(열 방정식)과 이를 좀 더 일반화 한 포커르-플랑크 방정식을 유도할 것 입니다. 지난 포스팅을 읽지 않으신 분이라면, 지난 포스팅 부터 순서대로 읽기를 권장합니다.
"같은" 랜덤 워크가 구현되는 공간, 시간 간격의 관계
지난 포스팅에서는 $D$차원 정수 격자 공간에서의 랜덤 워크를 알아봤습니다. 1차원 공간의 경우에서, 1번 스텝을 더 디딜 때 마다 $x_{n+1}$은 $x_n+1$이 되거나 $x_n-1$이 되었습니다. 즉 연속된 두 스텝의 위치의 차이 $x_{n+1} - x_n$는 1이었습니다. "격자" 공간을 생각했기 때문에 변화량은 자연스럽게 1이었고, 이는 $\Delta x = 1$로 표현할 수 있습니다. "스텝"은 정수 $n$으로 표현하였습니다. 스텝이 횟수는 시간으로 전환이 가능한데, $\Delta t$ 를 시간의 단위로 하여 한 시간 단위 마다 한 번 자리를 옮겼다고 하면, 스텝의 횟수와 총 시간은 $t = \Delta t N$ 와 같이 $t$와 $N$이 전환 됩니다. 따라서 이제 부터는 스텝의 횟수 $n$을 사용하는 대신에 $t$를 도입하여 스텝의 횟수를 나타낼 것 입니다. 당연히 $t = \Delta t N$이 됩니다. 지금까지는 스텝 $n$에서 위치를 $x_n$으로 수열을 나타내는 방식으로 썼는데, 이제 부터는 $x(t)$로 쓰도록 하겠습니다. 보통 $x(t)$와 같이 표기를 하면 $t$는 연속적인 값을 의미하는 경우가 많은데, 여기서 $t$는 연속적인 값은 아니며, $t \leftrightarrow n\Delta t$의 변환을 나타낸다고 생각하면 됩니다.
서로 다른 두 랜덤 워크 $x_1(t), x_2(t)$이 있다고 하겠습니다. 위에서 설명한 방식을 따르면 랜덤 워크는 공간 간격 $\Delta x$, 시간 간격 $\Delta t$를 이용하여 완전하게 기술 할 수 있고, 두 랜덤 워크는 각각 $(\Delta x_1, \Delta t_1)$, $(\Delta x_2, \Delta t_2)$의 (공간, 시간) 간격을 갖는 랜덤 워크라고 하겠습니다. 랜덤 워크 1, $x_1(t)$, 은 $\Delta t_1$의 시간 마다 $\pm \Delta x_1$만큼을 움직이며, 랜덤 워크 2, $x_2(t)$, 는 $\Delta t_2$의 시간 마다 $\pm \Delta x_2$만큼을 움직입니다.
만일 $\Delta x_2 = 2 \Delta x_1$ 일 때, 즉 랜덤 워크2에서 한 스텝에 움직이는 거리가 랜덤 워크1에서 한 스텝에서 움직이는 거리의 2배가 된다면, 랜덤 워크 1의 분포와 랜덤 워크 2가 "같은" 랜덤 워크가 되기 위해서는, $\Delta t_1$와 $\Delta t_2$는 어떤 관계를 가져야 할까요?

$\Delta t_1 = \Delta t_2 = 1$인 경우의 두 랜덤 워크 $x_1(t), x_2(t)$를 각각 1,000개의 경로를 생성하였습니다. 그냥 봐도 두 랜덤 워크는 "같지" 않습니다. $\Delta x_2$가 $\Delta x_1$의 $2$배를 가정하였기 때문에, $x_2(t)$의 변화의 정도가 더 큽니다. 이전 포스팅의 결과를 이용한다면, $x_2(t)$의 표준편차는 $\sigma_1 = \Delta x_2 \sqrt{\frac{t}{\Delta t}}$가 되지만, $x_1(t)$의 표준편차는 $\Delta x_1 \sqrt{\frac{t}{\Delta t}} = \frac{1}{2} \sigma_1$가 됩니다. 위 그래프를 봐도 $t = 1,000$에서 $x_1(t)$의 최대값은 대략 75 부근에 있지만, $x_2(t)$의 최대값은 대략 150 부근에 있어, $x_2(t)$가 원점에서 멀어지는 정도가 $x_1(t)$가 원점에서 멀어지는 정도의 2배가 됩니다. 한 스텝에 움직일 수 있는 거리가 2배 되었기 때문에 당연한 결과입니다.
두 랜덤 워크가 "같아"지려면, 임의의 $t$에서 $x(t)$의 표준편차 $\sigma$가 서로 같으면 됩니다. 시간 $t$에서 표준편차는 $\sigma(t) = \Delta x \sqrt{\frac{t}{\Delta t}}$와 같이 주어집니다. 따라서 표준편차가 같기 위해서는
$$\frac{\Delta x_1}{\sqrt{\Delta t_1}} = \frac{\Delta x_2}{\sqrt{\Delta t_2}}$$
의 관계가 만족 되어야 합니다. 즉, $\Delta t_1, \Delta t_2$는
$$\Delta t_1 = \Big(\frac{\Delta x_1}{\Delta x_2} \Big)^2 \Delta t_2$$
가 되어야 합니다. $\frac{\Delta x_1}{\Delta x_2} = \frac{1}{2}$ 를 가정하였기에, $\Delta t_1 = \frac{1}{4} \Delta t_2$가 됩니다. 공간의 간격이 절반으로 줄어들면, 시간의 간격은 그것의 제곱인 $\frac{1}{4}$으로 줄어들어야 합니다. 시간의 간격이 $\frac{1}{4}$로 되었기 때문에 동일한 시간 $t$동안 이동하는 스텝의 횟수는 $4$배 증가하게 되고 따라서 두 랜덤 워크의 시간에 따른 표준편차가 같아 지게 됩니다.
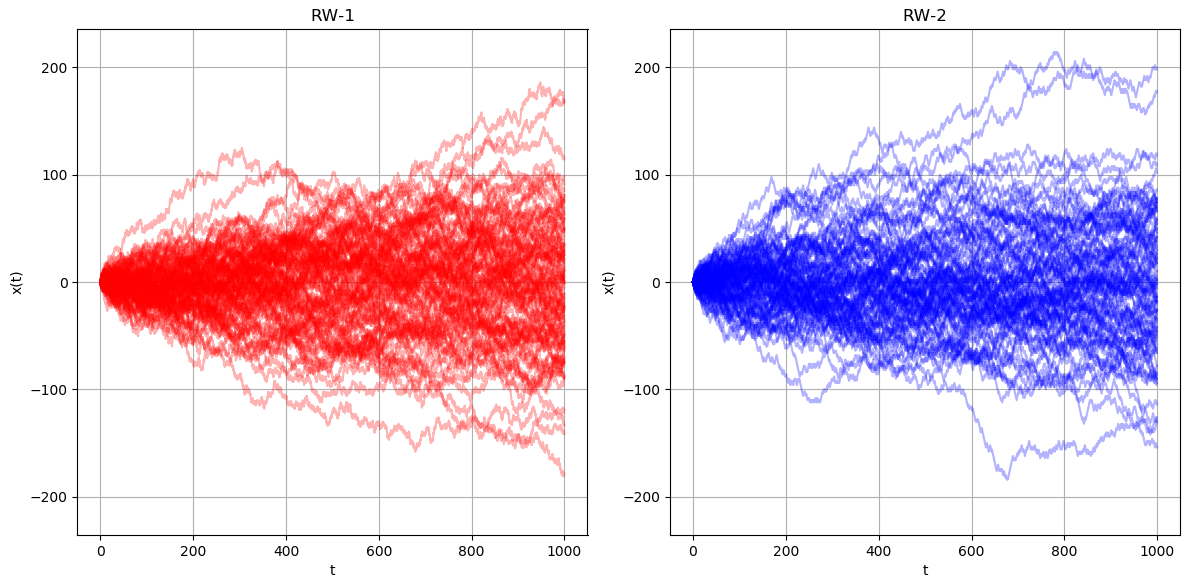
위 그래프는 $(\Delta x, \Delta t) = (1, \frac{1}{4})$ 인 랜덤 워크(왼쪽 빨간색 그래프)와 $(\Delta x, \Delta t) = (2, 1)$ 인 랜덤 워크(오른쪽 파란색 그래프)의 경로 1,000개를 구현한 것 입니다. 랜덤 워크의 확률성에 따라서 두 랜덤 워크의 구현이 완전히 똑같을 수는 없지만, 두 그래프는 같은 랜덤 워크가 구현된 것 처럼 보입니다.

위 그래프는 $(\Delta x, \Delta t) = (\frac{2}{3}, \frac{1}{9})$ 인 랜덤 워크 (왼쪽 녹색 그래프)와 $(\Delta x, \Delta t) = (\frac{1}{2}, \frac{1}{16})$ 인 랜덤 워크 (오른쪽 노란색 그래프)의 경로 1,000개를 구현한 것 입니다. 위 네 개의 랜덤 워크의
$$\frac{\Delta x}{\sqrt{\Delta t}}$$
의 값은 모두 $2$로 같습니다. 따라서 전체의 개형은 서로 같습니다.
시간과 공간의 연속화
공간의 간격과 시간의 간격의 제곱근의 비율 $\frac{\Delta x}{\sqrt{\Delta t}}$가 랜덤 워크의 모습을 결정합니다. $\frac{\Delta x}{\sqrt{\Delta t}} = 1$ 인 서로 다른 랜덤 워크를 생각한다면, 서로 다른 랜덤 워크는 하나의 값 $\epsilon$으로 기술이 가능한데, $\Delta x = \epsilon, \Delta t = \epsilon^2$로 놓을 수 있습니다.

위 그래프는 $\epsilon = 1$ 인 랜덤 워크 (왼쪽 빨간색 그래프)와 $\epsilon = 0.01$ 인 랜덤 워크 (오른쪽 파란색 그래프)의 경로를 구현한 것 입니다. $\epsilon = 1$의 경우 $\Delta t= 1$이기 때문에 위와 같이 $x$값 뿐 아니라 $t$값이 모두 $1$만큼의 불연속적인 값을 갖습니다. $\epsilon = 0.01$의 경우 $\Delta t= 0.0001$로 (물론 원리적으로는 당연히 불연속 이긴 하지만 그래프만 본다면) $x(t)$가 $t$에 대한 연속 함수인 것 처럼 보입니다. 즉 $t$가 연속적인 실수값을 갖고 $x(t)$역시 연속적인 실수 값을 갖는다고 근사할 수 있습니다.
$\epsilon \rightarrow 0$의 극한을 생각하면, $t$, $x$ 모두 연속적인 값을 갖게 되고, 랜덤 워크 $x(t)$는 시간에 대해서나 공간에 대해서나 연속적인 함수가 됩니다. 처음에 정의했던 랜덤 워크는 "1차원 격자 점에서 한 스텝씩 불연속적으로 움직"였는데, 시간의 간격과 공간의 간격이 무한소가 되는 극한을 생각하면 랜덤 워크는 "(연속적인 값을 갖는) 1차원 공간에서 시간에 따라 연속적으로 움직"이게 됩니다. 이 같은 성질 때문에, 불연속한 시간, 공간의 자유도를 갖는 방정식을 위에서 했던 것과 동일한 방식으로 연속적인 시간, 공간의 자유도를 갖는 방정식으로 바꿔 놓는 것을 "연속화" 라고 합니다. 위에서 우리는 랜덤 워크를 시간, 공간에 대해서 연속화 한 것 입니다.
"동일"한 대상(랜덤 워크)을 기술하는 시간적, 공간적 간격(스케일)에 따라서 대상을 기술하는 방식(불연속, 연속)이 바뀌게 된 것 입니다. $\epsilon$이 작은 경우는 대상의 움직임을 매우 정교하게 관찰하는 것에 해당하고, $\epsilon$이 매우 큰 경우는 그 반대로 대상의 움직임을 매우 성글게 관찰하는 것이 됩니다. 랜덤 워크의 좋은 예시라 할 수 있는 물 속에서 잉크 입자의 움직임을 우리의 관찰의 대상이라고 한다면, $\epsilon$이 작은 경우는 원자 수준의 스케일에서 잉크를 구성하는 원자의 움직임을 관찰하는 것 입니다. 이 경우 잉크를 구성하고 있는 원자의 위치는 주변에 있는 다른 잉크 입자나 물 분자와이 어지로운 충돌로 인해서 시간에 따라 매우 급격한 변화를 보일 것 입니다. 반대로 $\epsilon$ 이 큰 경우는 거시적인 수준(cm 단위)에서의 관찰에 해당하고 잉크 입자는 매우 부드럽고 완만하게 물에서 퍼져 나갈 것 입니다.
주방정식을 이용한 시간, 공간의 연속화
위에서는 랜덤 워크 프로세스 그 자체의 연속화에 대해서 다루었는데, 이번에는 랜덤 워크의 주방정식을 연속화 해 보도록 하겠습니다. 1차원 정수 격자 공간에서의 주방정식은
$$p(x, n+1) = \alpha p(x-, n) + (1- \alpha) p(x+1, n)$$
입니다. 여기서 $\alpha \in [0, 1]$은 랜던 워크가 치우쳐진 정도를 기술합니다. $\alpha = \frac{1}{2}$는 치우쳐지지 않은 랜덤 워크 입니다. 위에서와 같이 공간과 시간을 연속화 할 수 있는데, 우선 위 식에서 $n \rightarrow t$, $x \pm 1 \rightarrow x \pm l$로 "단위"를 변경하면 ($\Delta x$를 $l$ 로 둔 것 입니다.),
$$p(x, t + \Delta t) = \alpha p(x-l, t) + (1- \alpha) p(x+l, t)$$
가 됩니다. $p(x,t)$은 $x, t$에 대한 연속 함수 이기 때문에 (연속화를 하면 연속 함수가 됩니다), 테일러 전개를 이용하여 위 식을 표현하면,
$$p + \frac{\partial p}{\partial t} \Delta t = \alpha \Big(p - l \frac{\partial p}{\partial x} +\frac{1}{2} l^2 \frac{\partial^2 p}{\partial x^2}\Big) + (1- \alpha )\Big(p + l \frac{\partial p}{\partial x} +\frac{1}{2} l^2 \frac{\partial^2 p}{\partial x^2}\Big)$$
가 됩니다. 이 식을 잘 정리하면,
$$\frac{\partial p}{\partial t} = -v \frac{\partial p}{\partial x} + D \frac{\partial ^2 p }{\partial x^2}$$
가 됩니다. 이 식을 포커르-플랑크 방정식(Fokker-Planck equation)이라고 합니다. 여기서,
$$v = (2\alpha -1) \frac{l}{\Delta t}, D = \frac{l^2}{2 \Delta t}$$
로 각각 유동 속도(drift velocity), 확산 계수(diffusion coefficient) 라고 합니다.
유동 속도가 0인 포커르-플랑크 방정식 : 확산 방정식
포커르-플랑크 방정식에서 유동 속도 $v = 0$인 경우를 특히 확산 방정식(diffusion equation) 이라고 부릅니다. 확산 방정식은 열의 확산을 기술하는 방정식과 의미나 형태가 같기 때문에 열 방정식(heat equation) 이라고도 합니다. 열의 확산이나 입자의 확산의 근원이 같습니다.
확산 방정식을 다시 쓰면,
$$\frac{\partial p}{\partial t} = D \frac{\partial ^2 p }{\partial x^2}$$
로, (초기 상태에서의 밀도 $p(x, 0)$ 이 일치한다면,) 확산 계수 $D = \frac{1}{2} \frac{l^2}{\Delta t}$에 의해서 $p(x, t)$가 모두 결정 됩니다. 확산 계수에서 $\Delta t$는 랜덤 워크의 주기이며, $l$은 한 차례의 랜덤 워크에서 입자가 이동할 수 있는 거리의 단위 입니다. 앞 부분에서 "동일한 랜덤 워크"가 될 조건이
$$\frac{\Delta x^2}{\Delta t}$$
가 동일한 것이었는데, (여기서 $\Delta x$는 $l$과 같은 역할을 합니다) 이 값이 확산 계수의 2배가 된다는 것을 생각하면 당연한 결과라고 볼 수 있습니다.
확산 방정식의 해
확산 방정식은 $(x, t)$의 편미분 방정식입니다. 이러한 형태의 편미분 방정식은 주로 물리학의 응용 곳곳에서 등장하는데, 슈뢰딩거 방정식이나 파동 방정식이 중요한 예시 입니다. 가장 간단한 경우인 $p(x, 0) = \delta(x)$인 초기 조건에서 확산 방정식의 해가 시간의 변화에 따라서 어떻게 주어지는지 알아 보겠습니다. 해를 푸는 방식은 생략하고 답만 쓰면,
$$p(x,t) = \frac{1}{\sqrt{4\pi D t}}e^{-\frac{x^2}{4Dt}}$$
입니다. 정규 분포 함수
$$N(x)t = \frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{(x-\mu)}{2 \sigma^2}}$$
과 비교하면, $\mu = 0, \sigma = \sqrt{2Dt}$ 가 됨을 쉽게 확인할 수 있습니다. 즉 $x=0$에서 국소적으로 분포되어있던 확률(밀도)는 시간이 지나면서 정규 분포를 따르게 되는데, 표준편차가 $\sqrt{t}$에 비례하는 형태로 주어지게 됩니다.

위 그래프는 $D = 1$ 인 경우에서 $t$에 따른 $p(x,t)$를 그린 것 입니다. 실제로 $t=0.0$에서는 디락 델타 함수가 되지만, 그런 경우에는 그래프를 그릴 수 없어 $t = 0.01$값을 사용하여 그렸습니다.
$D = \frac{1}{2} \frac{l^2}{\Delta t}$를 대입하여 식을 조금 변형하면, $\sigma = l \sqrt{\frac{t}{\Delta t}} = l \sqrt{n}$ 이 됩니다. 이는 연속적인 공간, 시간에서 확산 방정식을 불연속적인 시간, 공간에서의 랜덤 워크로 변환한 결과가 됩니다. 랜덤 워크에서 $\sigma = l\sqrt{n}$ 로 주어졌는데, (당연하게도) 같은 결과를 얻습니다. 같은 프로세스를 기술하는 시간-공간의 단위(연속, 불연속)에 따라 서로 다르게 기술 한 것일 뿐, 최종적으로 "관찰"할 수 있는 결과는 당연히 같아야 합니다.

위 그래프는 지난 포스팅에서 주방정식의 풀이를 통해 얻은 확률 밀도 함수 $p(x, n)$ 입니다. 위 계산에서는 시간-공간은 불연속적이었습니다. 따라서 확률 밀도 함수 값이 띄엄 띄엄한 값을 갖게 되는데, 확산 방정식의 해는 랜덤 워크의 시간-공간을 연속화 조건에서 확률 밀도 함수이기 때문에 연속적인 정규분포를 갖게 됩니다. 앞서 언급한 바와 같이, 해의 개형은 당연히 같은데, 시간(스텝)과 공간을 기술하는 방식의 차이에서 해의 차이가 생깁니다.
2차원 공간에서 확산 방정식
1차원 공간에서 확산 방정식을 얻었던 식에서 $x$ 성분 뿐 아니라 $y$ 성분을 추가하면 2차원 공간에서의 확산 방정식을 얻을 수 있습니다. 편의상 치우쳐지지 않은 랜덤 워크($\alpha = \frac{1}{2}$)를 생각하면, 주방정식을 연속화 하는 단계에서
$$p(x,y, t + \Delta t) = \frac{1}{4} \Big( p(x + l, y, t) + p(x -l,y, t) + p(x, y+l, t) + p(x, y-l, t) \Big)$$
를 전개하면 됩니다. 여기서 중요한 점은 우항의 괄호 앞에 있는 계수가 $\frac{1}{2}$가 아닌 $\frac{1}{4}$라는 것 입니다. 이전 포스팅에서도 여러번 설명하였는데, 2차원 공간의 경우 입자가 움직일 수 있는 방향이 1차원 공간에 비해 2배 만큼 많아졌기 때문에 계수는 그에 반비례하는 $\frac{1}{4}$가 됩니다. 식을 전개 하고 정리하면 2차원에서의 확산 방정식은
$$\frac{\partial p}{\partial t} = D \Big(\frac{\partial ^2 p}{\partial x^2} + \frac{\partial ^2 p}{\partial y^2} \Big) = D \nabla^2 p$$
가 됩니다. 여기서 $D$는 역시 확산 계수로 $D = \frac{1}{4}\frac{l^2}{\Delta t}$이 됩니다. 위 식에서 괄호 앞의 $\frac{1}{4}$가 확산 계수에서 $\frac{l^2}{\Delta t}$의 계수가 된 것 입니다.
가장 간단한 경우인 $p(x,y,0) = \delta(x)\delta(y)$ 인 초기 조건에서 위 확산 방정식의 해를 구하면
$$p(x, y, t) = \frac{1}{4 \pi D t} e^{-\frac{r^2}{4Dt}}$$
가 됩니다.
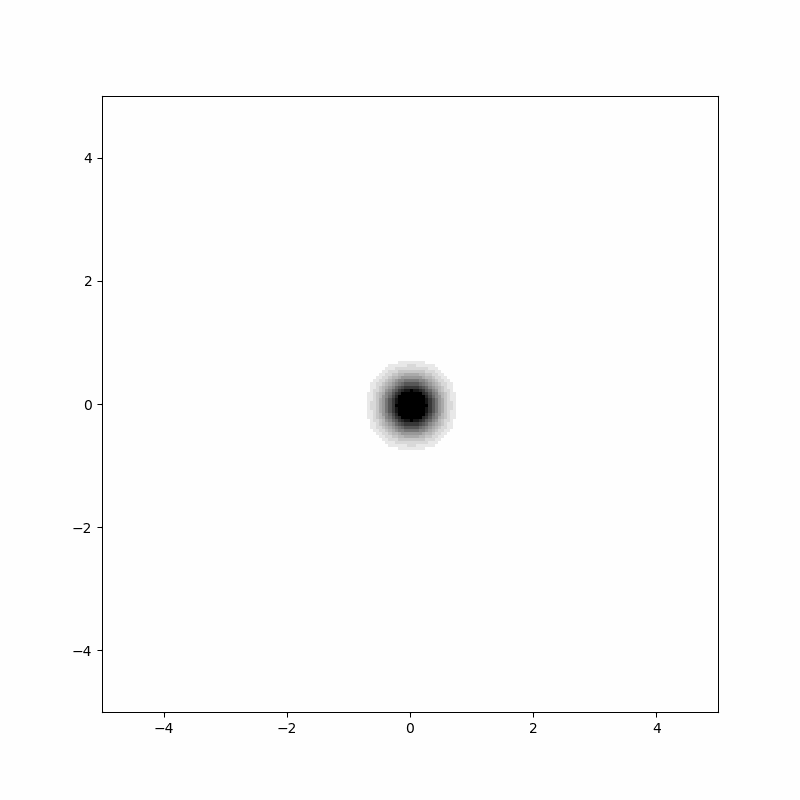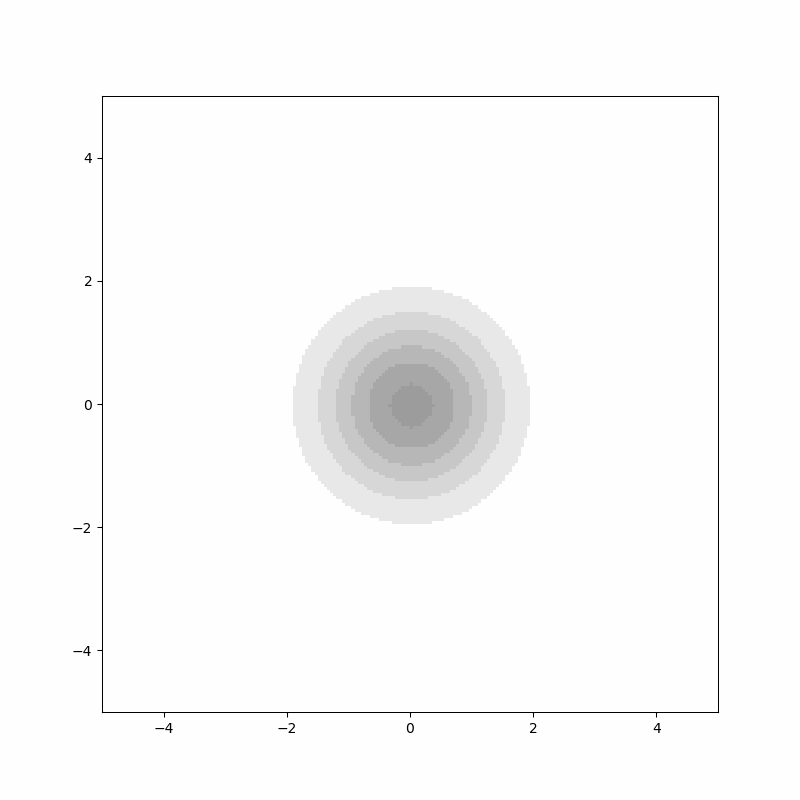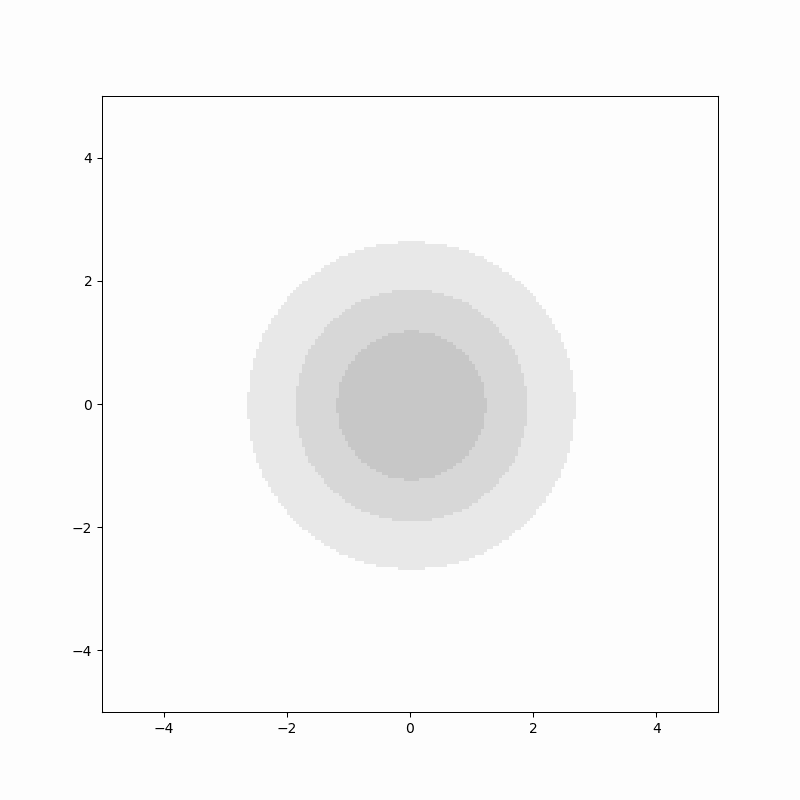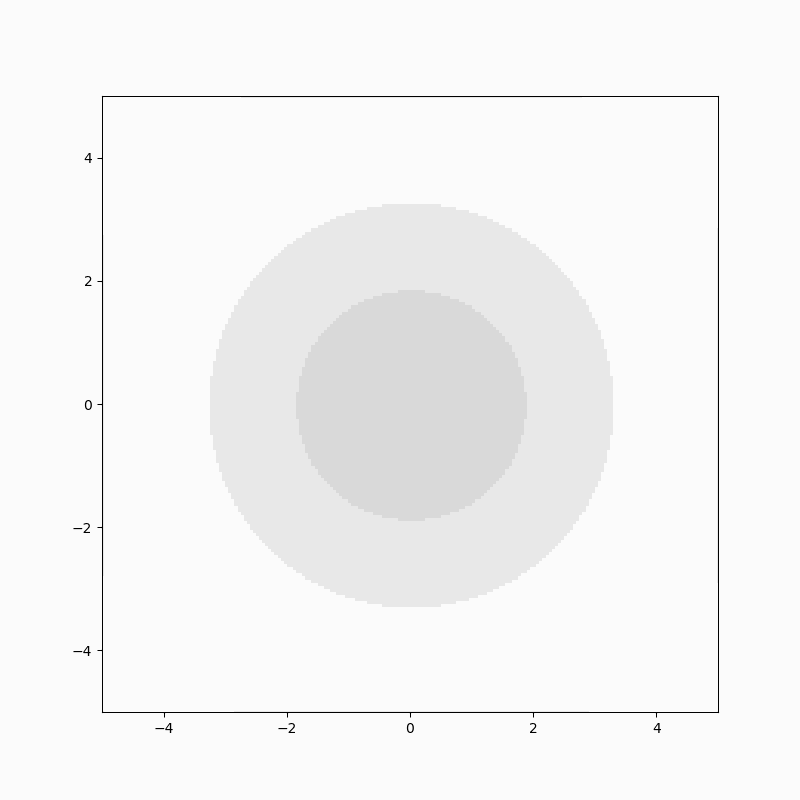
위 애니메이션은 2차원 확산 방정식의 해를 보여줍니다. 진한 부분이 $p(x,t)$값이 큰 부분입니다. 원점에 국한 돼 있던 밀도가 시간이 흐름에 따라서 등방적으로 퍼저나가는 것을 보여주고 있습니다.
확산 계수를 다시 살펴 보자
확산 방정식에는 단 하나의 상수, 확산 계수 $D$가 있습니다. 초기 조건이 같은 경우, 오직 확산 계수만이 시간에 따른 해의 변화를 결정할 뿐 입니다. 확률 밀도 함수에서 "확산의 정도"를 나타내는 표준 편차 $\sigma \propto \sqrt{D}$ 로 부터, 확산 계수가 클 수록 확률 밀도 함수가 공간상으로 더 빠르게 퍼져 나감을 알 수 있습니다.
랜덤 워크를 기술하는 시간, 공간의 단위를 유한한 단위에서 무한소의 단위로 "연속화" 시켜서 확산 방정식을 얻었습니다. 물리학에서는 이를 두고, 같은 현상을 미시적, 거시적으로 기술한다고 하는데, 확산 방정식은 "확산"이라는 현상을 거시적인 과점에서 현상적으로 기술하는 것이고, 랜덤 워크는 "확산"이라는 현상을 미시적인 관점에서 모델링 한 것 입니다. 미시적인 관점과 거시적인 관점을 연결하는 "고리"는 $D = \frac{1}{2 d} \frac{l^2}{\Delta t}$ 라는 식 입니다. 우변은 미시적인 관점(랜덤 워크)을 기술하는 파라미터이고, 좌변은 거시적인 관점(확산 방정식)을 기술하는 파라미터입니다. $D$를 통해서 $l, \Delta t$를 유추할 수 있고, 반대로 $l, \Delta t$를 통해서 $D$를 계산할 수 있습니다.
확산 계수를 통한 미시 세계와 거시 세계의 연결
기체에서의 확산을 생각해 보겠습니다. 예를들어서 향수의 향기 입자의 확산을 생각할 수 있습니다. 기체 분자들의 어지로운 운동에서 특정 향기 입자의 움직임만을 본다면, 이는 거의 랜덤 워크라고 할 수 있을 정도로 무작위적으로 움직일 것 입니다. (물론 보다 근원적인 방정식인 뉴턴의 운동 방정식을 생각한다면, 입자의 움직임은 무작위가 아니라 정확히 법칙에 이해서 움직이는 결정론적인 움직임 입니다) 이를 랜덤 워크로 본다면, 랜덤 워크의 스텝의 주기 $\Delta t$는 기체 분자의 충돌과 충돌 사이의 시간(이를 $\tau$ 라고 쓰겠습니다)이 되고, 한 스텝에서 움직이는 공간적인 거리 $l$은 평균 자유 이동 거리 (mean free path, $l_p$) 가 될 것 입니다. 따라서 확산 계수는 $D = \frac{l_p^2}{\tau}$가 됩니다. 여기서, 기체 분자들의 평균 속도를 $v$라고 한다면, $l_p = v \tau$가 되고 확산 계수는 $D = v^2 \tau$로도 쓸 수 있습니다. 기체 분자들의 평균 속도는 맥스웰-볼츠만 분포를 통해 구할 수 있는데, $v = \sqrt{\frac{3k_BT}{m}}$ 입니다. 여기서 $m$은 질량, $k_B$는 볼츠만 상수, $T$는 온도 입니다.
만일 우리가 실험을 통해서 확산 계수 $D$를 구할 수 있다고 한다면(이는 시간에 따른 향기 입자가 확산된 거리를 통해서 구할 수 있습니다), 이를 통해서 미시적인 물리량인 기체 분자의 운동에서 충돌과 충돌 사이의 시간 $\tau$를 구할 수 있습니다. 즉, 거시적인 실험을 통해서 미시적인 물리량을 유도할 수 있는 것이죠! 반대로 원자 시뮬레이션(모델링)을 통해서 $\tau$를 구할 수 있다면, 이를 통해서 거시 세계의 현상을 설명하는 확산 계수 $D$를 예측할 수 있습니다. "랜덤 워크 - 확산 방정식"의 예시처럼 물리 방정식(프로세스)에서는 동일한 현상을 미시적-거시적인 관점에서 기술하는 방정식의 짝이 있습니다. 이번 포스팅에서 알아본 경우는 그 중에서도 가장 직관적이면서도 간단한 경우로 거시적인 현상과 미시적인 법칙이 어떠한 관계를 통해서 연결 될 수 있는지를 매우 잘 보여주는 좋은 예시 입니다.
일반적인 포커르-플랑크 방정식
랜덤 워크의 주방정식을 연속화 하여 포커르-플랑크 방정식을 유도하였습니다. 위에서는 특수한 경우라고 할 수 있는 확산 방정식에 대해서 알아보았습니다. 보다 일반적인 경우의 포커르-플랑크 방정식의 해에 대해서는 다음 포스팅을 통해서 좀 더 구체적으로 알아 보도록 하겠습니다.
'수학' 카테고리의 다른 글
| 포물선의 반사의 성질 : 축에 나란한 방향으로 입사한 빛은 반드시 포물선의 초점을 지난다 (3) | 2023.04.06 |
|---|---|
| 중심 극한 정리 (CLT : Central Limit Theorem) : 여러개를 뽑아서 평균을 내면 정규 분포와 유사해 진다 (0) | 2022.05.16 |
| 무작위 걸음(랜덤 워크 random walk) 103 : 주방정식(Master equation)을 이용한 시간에 따른 랜덤 워크의 확률 밀도 함수 계산 (0) | 2022.05.07 |
| 무작위 걸음(랜덤 워크 random walk) 102 : 앙상블 평균과 몬테 카를로 시뮬레이션 (1) | 2022.05.01 |
| 무작위 걸음(랜덤 워크 random walk) 101 : 파이썬 프로그램으로 구현 (0) | 2022.04.29 |



