포물선의 반사의 성질 : 축에 나란한 방향으로 입사한 빛은 반드시 포물선의 초점을 지난다

이번 포스팅에서는 포물선의 광학적 성질 중 하나인 "포물선의 축에 나란한 방향으로 입사한 빛은 포물선에 반사 후, 포물선의 초점을 지난다"를 증명해 보도록 하겠습니다. 
 
포물선의 방정식
 
우선 포물선의 정의와 초점의 정의를 돌이켜 보도록 하겠습니다. 포물선은 "한 점과 그 점을 지나지 않는 한 직선에 이르는 거리가 같은 그 점과 그 직선을 포함하는 평면 위의 점의 자취" 입니다. 

위키피디아

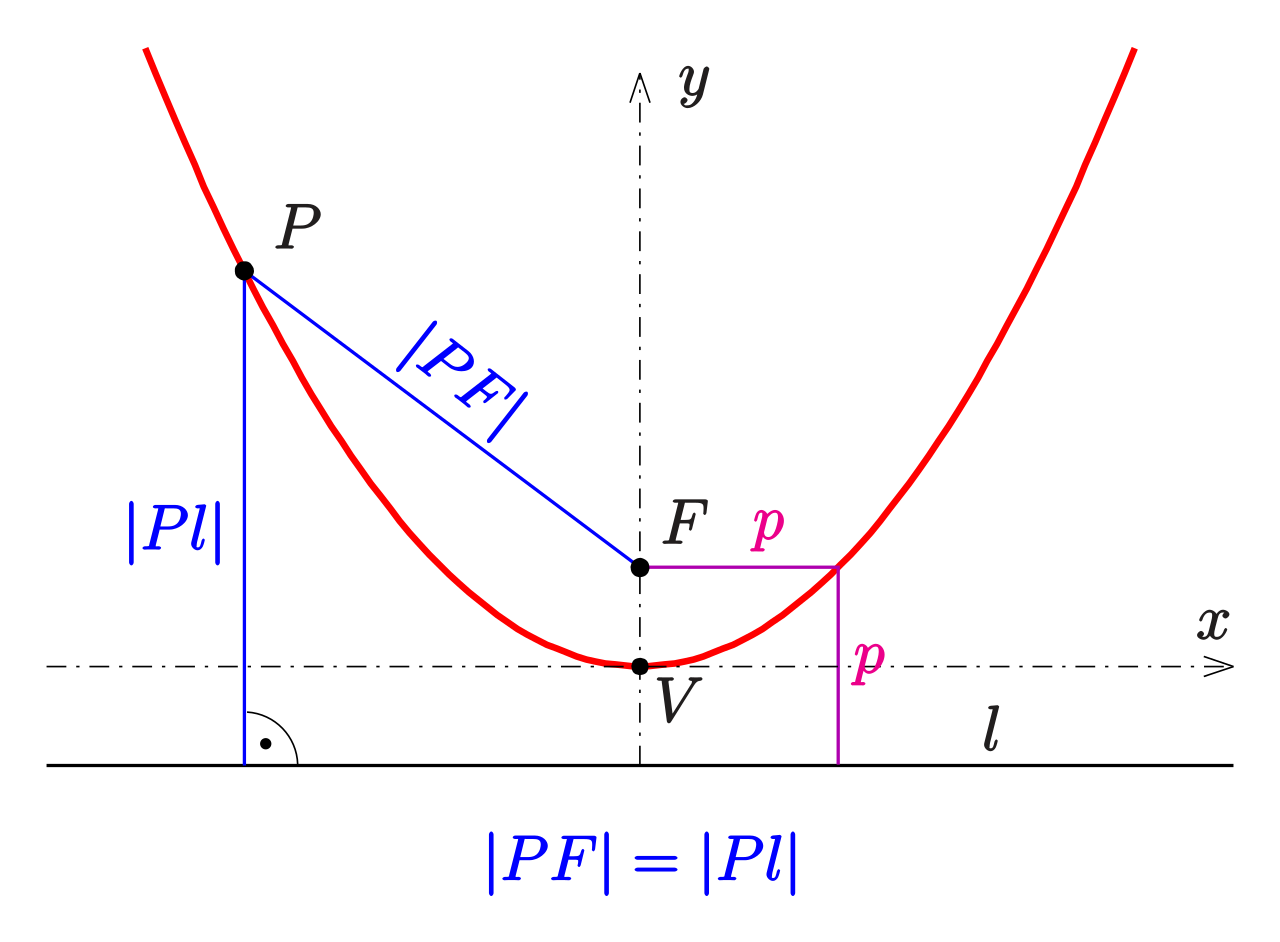
위 정의에서 한 점은 $F$이고 (이 점의 좌표를 (0, f)라 하겠습니다.), 이 점을 지나지 않는 직선은 $l$ (포물선의 정의에 따라 이 선의 $y$ 좌표는 $-f$ 입니다) 입니다. 이 직선을 보통 "준선" 이라고도 합니다. 포물선 위의 한 점을 $P$라고 한다면, 포물선의 정의에 따라서, 선분 $PF$의 길이와 선분 $Pl$의 길이가 같아야 합니다. 점 $P$의 좌표를 $(x,y)$라고 한다면,
$$|PF| = \sqrt{x^2 + (y-f)^2} = |Pl| = (y+f)$$
로 부터, 
$$y = \frac{1}{4f}x^2$$
를 얻습니다. 위에서 정의한 점 $F$를 포물선의 초점이라고 하고, 초점 거리는 $f$가 됩니다.
 
반사의 법칙
 
반사의 법칙은 간단합니다. "입사각 = 반사각" 만 외우면 됩니다. 보다 일반적인 경우의 반사와 굴절 등에 대한 물리적 법칙은 이전 포스팅
https://studyingrabbit.tistory.com/85

빛의 진행 경로와 페르마의 원리와 Eikonal(아이코널) 방정식 : 페르마의 원리로  부터 스넬의 법칙

을 참고하면 됩니다 (근데, 그러고 보니 위 글을 굴절에 대한 것이고, 반사에 대한 설명은 없네요 ㅎㅎ)

평면을 향해 입사하는 빛이 반사하는 경우를 생각해 보도록 하겠습니다. 입사하는 빛의 방향은 위 그림에서 하늘색 화살표로 표시하였고, 반사하는 빛의 방향은 위 그림에서 녹색 화살표로 표시하였습니다. 그리고 반사 하는 평면에 수직한 법벡터는 빨간색으로 표시하였습니다. 입사 벡터, 반사 벡터, 법 벡터를 모두 정규화(크기를 1로) 시킨 벡터를 각각 $\vec{d}_i, \vec{d}_s, \vec{d}_n$ 이라고 하겠습니다. 입사 벡터와 법 벡터를 알고 있으면 반사의 법칙에 따라서 반사 벡터를 구할 수 있는데, 간단한 기하학적 논의에 의해
$$\vec{d}_s = \vec{d}_i - 2 \vec{d}_n (\vec{d}_n \cdot \vec{d}_i)$$
가 됩니다. 
 
이제 포물선의 성질(포물선의 방정식과 초점의 정의)과 반사의 법칙(반사 하는 빛의 방향)을 알았으니, 해석 기하학의 방법을 통해서 포물선의 독특한 광학적(반사에 의한) 성질을 증명해 보도록 하겠습니다.
 
포물선의 축과 나란하게 입사한 빛은 포물선에 반사 후, 반드시 초점을 지난다.

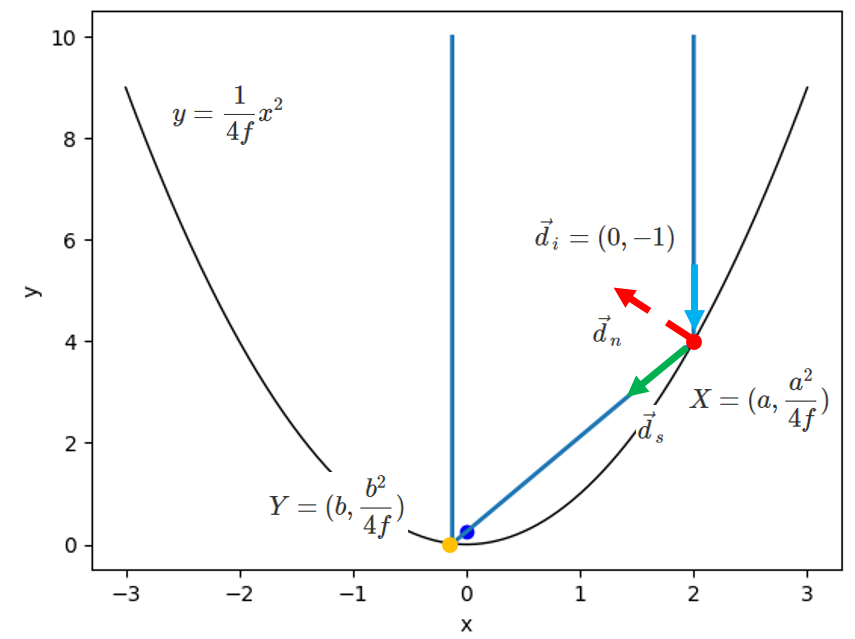
 위 그림에서와 같이 $x = a$ 에서 빛이 입사 했다고 하겠습니다. 입사 빛은 $y$ 축과 나란하기 때문에 $\vec{d}_n = (0, -1)$가 됩니다. $y = \infty$에서 입사한 빛은 점 $X = (a, \frac{a^2}{4f})$ 에서 반사하게 됩니다. 반사 벡터 $\vec{d}_s$를 구하기 위해서는 반사가 일어나는 지점의 법벡터 $\vec{d}_n$를 알아야 하는데, 법벡터는 점 $X$에서의 접선에 수직인 벡터가 됩니다. 
 
점 $X$에서 접선의 기울기는 $y = \frac{x^2}{4f}$를 미분하고 $x = a$를 대입하면 얻어 지는데, 기울기는 $\frac{a}{2f}$가 됩니다. 이 접선에 나란한 단위 벡터는 $\frac{1}{\sqrt{1 + \frac{a^2}{4f^2}}}(1, \frac{a}{2f})$가 됩니다. 편의상 이 벡터를 $\vec{d}_m$으로 쓰도록 하겠습니다. (이 벡터는 위 그림에 표시하지 않았습니다)
 
$\vec{d}_m$를 시계 방향으로 $90$도 만큼 회전 시키면 우리가 원하는 법벡터 $\vec{d}_n$를 얻게 됩니다. 벡터의 회전은 회전을 기술하는 행렬
$$\begin{pmatrix}\cos(\theta)&\sin(\theta)\\-\sin(\theta)&\cos(\theta)\end{pmatrix}$$
를 이용하면 쉽게 구할 수 있는데, 이로 부터 
$$\vec{d}_n = \frac{1}{\sqrt{1+\frac{a^2}{4f}}}(-\frac{a}{2f}, 1)$$
을 얻습니다. $\vec{d}_m$과 $\vec{d}_n$이 수직이기 때문에 두 벡터의 내적이 0이 되는 것은 쉽게 확인할 수 있습니다. 
 
$\vec{d}_i$와 $\vec{d}_n$을 알았으니, $\vec{d}_s$는 식에 따라서 쉽게 얻을 수 있습니다. 계산을 하면,
$$\vec{d}_s = \frac{1}{1+\frac{a^2}{4f^2}} (-\frac{a}{f}, 1 - \frac{a^2}{4f^2})$$
를 얻습니다. 
 
반사파의 방향 벡터를 알았으니, 반사하는 직선에 해당하는 기울기를 구할 수 있는데, 이를 $m$으로 두면,
$$m = \frac{d_{s, y}}{d_{s, x}}$$
가 됩니다. 여기서 $d_{s, x}, d_{s, y}$ 는 반사 벡터 $\vec{d}_s$의 $x, y$ 성분입니다. 값을 직접 대입하여 정리하면,
$$m = -\frac{f}{a} + \frac{a}{4f}$$
가 됩니다. 
 
반사하는 직선의 기울기($m$)와 이 직선이 지나가는 점 ($X$)를 알았으니, 이 직선의 직선의 방정식을 구할 수 있는데,
$$y = \Big( -\frac{f}{a} + \frac{a}{4f}\Big)(x-a) + \frac{a^2}{4f}$$
가 됩니다. 이 직선과 $y$축이 만나는 점을 점을 구하면, 위 직선의 방정식에서 $x = 0$을 대입하면 되는데, 그 결과는
$$(0, f)$$
가 됩니다. 즉, $a$값에 상관 없이, 반사 하는 직선은 $(0, f)$ 점을 지나게 됩니다. 이 점은 바로 포물선의 초점 입니다. (증명 끝)
 
위 증명에서는 포물선의 방정식이 $y = \frac{1}{4f}x^2$으로 주어진 다는 것을 활용하였습니다. 인터넷을 검색하면 포물선의 정의를 활용하는 기하학적인 증명을 쉽게 확인할 수 있습니다. 저는 똑똑하지 않아서 논증 기하적인 증명은 어려워서, 계산은 좀 해야하지만 좀 더 기계적으로 증명할 수 있는 해석 기하학의 방법을 택했습니다. 해석 기가학적 증명을 하면, 단순히 우리가 증명하려는 것 뿐 아니라, 그 이상의 성질들도 쉽게 유도할 수 있다는 장점이 있습니다. 
 
$x = a$ 로 입사한 빛은 어디로 반사되어 나아갈까?
 
위에서는 입사하는 빛이 포물선의 축과 나란하기만 하다면 반사된 빛은 반드시 초점을 지난다는 것을 증명하였습니다. 한 번 반사된(점 $X$에서 반사) 빛은 또 다시 반사하게(점 $Y$에서 반사) 되고, 그렇게 반사된 빛은 입사할 때와는 반대 방향으로 반사되어 무한이 나아갑니다. 최종적으로 반사된 빛의 $x$좌표를 $b$라고 한다면 (위 그래프 그림에서 오렌지색으로 표시한 점 $Y$ 입니다.), $a$와 $b$의 관계는 어떻게 될까요? 즉, 우리의 문제는 "$x = a$로 입사한 빛은 $x= b$로 반사되어 나간다"에서 $b$를 $a$의 함수로 찾는 것 입니다.
 
이 문제는 비교적 간단하게 해결 할 수 있는데, 점 $X$와 점 $(0, f)$를 지나는 직선과 포물선의 교점을 구하면 됩니다. 직선의 방정식을 먼저 구하면 
$$y = \frac{1}{a} \Big( \frac{a^2}{4f} -f\Big)x + f$$
가 됩니다. 이 직선과, 포물선 $y = \frac{x^2}{4f}$의 교점을 구해야 하니,
$$\frac{1}{a} \Big( \frac{a^2}{4f} -f\Big)x + f = \frac{a^2}{4f}$$
방정식의 해를 구하면 됩니다. 2차 방정식이니 식을 정리하고 근의 공식을 쓰면,
$$x = \frac{1}{2} \Big[ a - \frac{4f^2}{a} \pm \Big|a + \frac{4f^2}{a} \Big| \Big]$$
를 얻습니다. $\pm$ 에서 $+$ 인 경우의 해는 $x = a$가 되는데, 이것은 점 $X$를 의미하여, 부호가 $-$인 경우가 우리가 찾으려는 $b$의 $x$ 좌표 입니다. $b = -\frac{4f^2}{a}$ 를 얻습니다.