지난 포스팅 <하이젠베르크는 어떻게 행렬역학을 유도하였나?> 에서는 베르너 하이젠베르크의 1925년 논문을 살펴보았습니다. 해당 논문에서 하이젠베르크는 고전역학에서는 단순 실수값을 가지던 "위치" 라는 물리량을 인덱스가 2개를 갖는 값으로 바꾸어 놓았습니다. 또한 인덱스가 2개인 값의 곱셈이 어떻게 표현되는지도 정의하였습니다. 그 당시의 하이젠베르크는 자신이 정의한 "인덱스가 2개인" 수학적인 대상이 행렬이라는 것을 알지 못했고, 따라서 그의 논문에는 "행렬(matrix)" 라는 단어가 전혀 등장하지 않았습니다. 행렬이라는 수학적 실체에 대해서 알지 못 했으니, 하이젠베르크는 그의 첫 논문에서 자신이 정의한 "인덱스가 2개인" 수학적인 대상에 대한 수학적인 체계에 대한 설명을 하지 못 하였습니다.
하이젠베르크의 논문은 독일의 저널 <Zeitschrift für Physik>에 1925년 7월 29일에 투고 되었습니다. 하이젠베르크의 지고 교수였던 막스 보른(Max Born)은 하이젠베르크의 논문의 중요성을 인식하였고, 그의 또 다른 제자인 파스쿠알 요르당(Pascual Jordan 정확한 발음의 한글 표기가 이와 같은지 모르겠으나, 이 같이 표현하도록 하겠습니다)와 함께 하이젠베르크의 논문은 연구하고 수학적으로 체계적인 형태로 발전시켰습니다. 그리고 약 2달이 흐른 1925년 9월 27일, 같은 저널에 투고하였습니다. 위 저널의 홈페이지에서 해당 위 두 논문의 정보를 찾으면, 두 논문의 투고일은 정확히 나와 있지만, 각 저널이 출판된 시점은 단순히 1925년 12월이라고만 나와 있습니다. 정확한 시점은 언제인지 모르겠으나, 두 논문은 약 2달 간격으로 저널에 투고되었고 1925년말에 정식적으로 출판되었습니다.
이번 포스팅에서는 보른과 요르당의 논문 <On Quantum Mechanics>을 읽어 보도록 하겠습니다. 이전 포스팅에서 소개한 바 있는 양자역학의 초기 논문의 영문 번역집 <Source of Quantum Mechanics>에 나와 있는 영문 번역본을 기본 텍스트로 삼을 것 입니다. 제목의 독일어 원문은 <Zur Quantenmechanik>로 독일어를 전혀 하지 못하지만 이 독일어를 영문으로 번역하면 <On Quantum Mechanics>이 된다는 것을 알 수 있을 것 같습니다.
초록

위 논문의 초록을 우리말로 (발)번역하면 대충....
"최근에 출판된 하이젠베르크의 이론적인 방법론을 행렬이라는 수학적인 방법론을 통해 체계적으로 발전시켰다. 변분원리로 부터 운동 방정식이 유도 됨을 보일 것이며, 하이젠베르크의 양자화 조건과 운동 방정식을 이용하여 에너지 보존 법칙과 보어의 에너지(주기) 조건이 유도 됨을 보일 것이다. 비조화진동자 예시를 활용하여, 해의 유일성에 대해 논의하고, 부분 진동의 위상의 중요성에 대해 논의할 것이다. 또한 전자기법칙을 양자역학에 적용하려는 시도를 다룰것이다." 입니다. 가장 핵심적인 내용은 초록의 첫 줄에 나와 있듯 "행렬을 활용하여 하이젠베르크의 방법론을 체계적으로 발전시키는 것" 입니다. 앞서 설명하였듯, 하이젠베르크의 논문에서는 "2개의 연산자를 가지는 양"이 수학적으로 어떤 것인지에 대해서 아무런 설명을 하지 않았습니다. 보른은 이 양이 행렬이라는 것을 알아 냈고, 행렬이라는 수학적인 언어(방법론)을 통해서 하이젠베르크의 방법을 다시 한 번 전개하게 됩니다.
논문의 서론 부분에는 하이젠베르크의 최근 논문에 대한 설명이 나와 있습니다. 하이젠베르크의 논문에 나온 "두 물리량의 곱셈의 법칙"이 다름이 아닌 "행렬의 곱셈 법칙"이라는 것을 지적합니다.
논문의 본문은 크게 3개의 챕터로 이루어져 있는데
(1) Matrix Calculation
(2) Dynamics
(3) Investigation of the anharmonic oscillator
입니다. 논문의 1/3이자 첫 시작 부분에는 행렬이 무엇인지, 행렬의 사칙연산이 어떻게 정의되는지에 대해 설명합니다. 특히 행렬의 곱과 미분에 대해서 중점을 두어 설명합니다.
이 당시에는 물리학 연구에서 행렬을 도입하는 것이 그렇게까지는 대중적인 방법은 아니었다고 합니다. 현대에는 고등학교 수학에서 행렬에 대해서 배우지만, 100년전에는 적어도 물리학계에는 행렬에 대한 공부가 필수적인 것은 아니었는것 같습니다. 하지만 한가지 의문이 드는 것은, 100년전이라고 하더라도 고전역학 시간이나 전자기학 시간에 벡터 공간에 대해서는 배울 것이고, 벡터 공간에 대해서 배우면 행렬에 대해서도 당연히 배울 것 인데, 하이젠베르크가 행렬에 대해서 전혀 몰랐다는 것은 약간은 신기 하기도 합니다. 하이젠베르크가 열심히 공부를 하지 않았을 것은 아니니, 그 당시 (적어도 학부생 수준의) 물리학자들에게 행렬은 그리 친숙한 개념은 아니었나 봅니다.
(1) Matrix Calculation
해당 챕터에서는 행렬곱의 미분에 대해서 자세하게 설명하고 있는데, 저도 행렬곱의 미분에 대해서는 그리 많이 접해보지 않아서 이에 대한 정의와 특징이 약간 생소하긴 합니다. 보통 행렬을 미분하는 것이면, 행렬의 각 성분을 미분하는것이 익숙한데, 이 논문에서는 행렬곱으로 이루어진 식을 행렬로 미분하는 것을 어떻게 하는지에 대해 정의하고, 이와 관련된 몇 가지 중요한 법칙을 소개합니다.

예를들면 위와 같습니다. 위치, 운동량 등 모든 물리량이 행렬로 표현되고, 해밀토니안과 같이 중요한 물리량이 행렬의 사칙연산으로 표현되기 때문에 행렬을 인수로 하는 함수를 행렬로 미분하는 것을 반드시 정의해야 합니다. 고전역학에서 $\frac{\partial H}{\partial x}$의 계산을 양자역학적으로 표현하기 위해서 행렬 함수를 행렬로 미분하는 것이 필요합니다. 식 (14)의 정의가 논문 전체를 걸쳐 매우 중요합니다.

친절하게도 위와 같이 예시도 들어 줍니다. 보통의 물리량, 특히 해밀토니안, 은 위치와 운동량의 다항식으로 표현됩니다. 따라서 위 예시와 같이 행렬의 다항식을 행렬로 미분할 때 결과가 어떻게 되는지가 중요합니다. 이 때문에,



위와 같이, 어떤 값 $z$가 행렬 $p, q$의 일반적인 다항식 꼴로 주어졌을 때, 미분이 어떻게 표현되는지를 자세하게 설명합니다. 이 중에서도 식 (22)와 같이 $d_1, d_2$가 정의 될 때, $d_1 + d_2 = 0$이 되는 것이 매우 중요합니다.
(2) Dynamics
이 챕터에서는 하이젠베르크의 방법론을 행렬을 이용하여 보다 체계적으로 설명합니다. 또한 오늘날 우리가 정준 교환 관계(cononical commutation relation 혹은 fundamental commutation relation)이라고 부르는 양자역학에서 가장 중요한 관계식인 $[\hat{x}, \hat{p}] = i \hbar I$ 가 이 챕터에서 유도됩니다. 지난 포스팅에서도 설명한 바 있는데, 하이젠베르크의 논문에서 하이젠베르크는 위치라는 물리량이 행렬을 통해서 표현될 수 있다(물론 하이젠베르크는 행렬이라는 단어를 언급하지 않았습니다)를 주장하였고, 물리량의 곱셈이 어떻게 되는지, 그리고 위치행렬의 대각성분이 어떠한 조건을 만족 시켜야 하는지에 대해서 설명하였습니다. 하이젠베르크의 논문에서는 $[\hat{x}, \hat{p}] = i \hbar I$가 등장하지 않습니다! 보통 $[\hat{x}, \hat{p}] = i \hbar I$를 두고 "하이젠베르크의 교환법칙"이라고 부르기도 하는데, 정확히 하자면, 이 교환법칙은 보른-요르당 교환법칙 이라고 해야한다고 생각합니다.

이 챕터의 시작 부분에서 위치와 운동량 행렬이 식 (24)와 같이 표현됨을 밝힙니다. 또한 $p, q$의 일반적인 함수로 주어지는 행렬 $g = g(p,q)$는

와 같이 표현됨을 설명합니다. 운동방정식이라는 것은 위치와 운동량이 시간에 따라 어떻게 변화하는가에 대한 식이니, 이 행렬들의 시간에 대한 미분은 매우 중요한데, 당연하게도 $g$의 시간에 대한 미분은
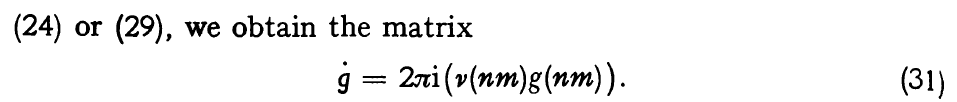
가 됩니다. 현대의 용어로 옮기자면, 행렬의 각 성분별로 시간에 대해 미분을 하는 것 입니다. 위 식 (29)에서 행렬 $g$의 각 성분의 시간에 대한 변화는 모두 지수함수에 의해 결정 됩니다. 행렬 성분 $g(nm)$은 상수로 취급 됩니다.
만일 행렬 $g$가 시간의 변화에 무관하다면, 즉, $\dot{g} =0$이라면, $v(nm) \ne 0$ 일 때, $g(n,m)=0$이 되어야 합니다. 축퇴가 없는(non-degenerate) 시스템을 생각하면, $n \ne m$ 이면 $v(nm) \ne 0$이 되고, $\dot{g} =0$ 이면 $g$는 대각행렬이 됩니다. $n \ne m$ 인 $(nm)$ 성분이 0이 되려면 $v(nm) = 0$ 혹은 $g(nm) = 0$이 되어야 하는데, $n \ne m$를 가정하였으니 당연히 $g(nm) = 0$, 즉, 행렬 $g$는 대각행렬이어야 합니다. 이는 성질은 논문 전체에 걸쳐 매우 중요한 역할을 합니다.
행렬 $p, q$가 만족해야 하는 "양자화 조건"은 하이젠베르크가 얻어낸 양자화 조건을 그대로 사용합니다.

아무래도 보른은 하이젠베르크의 지도 교수이니, 하이젠베르크 보다 고전역학에 대한 지식이나 수학에 대한 지식이 풍부했는지, 하이젠베르크의 논문 보다 조금 더 세련된 방법으로 양자화 조건을 표현합니다.

이 부분은 하이젠베르크가 얻어낸 양자화 조건과 일치합니다. 앞서 언급한 것 처럼 조금 더 새련된 방법으로 전개한 것이고, 하이젠베르크의 표현법과의 차이를 꼽는다면 $\dot{q}$ 대신에 $p$를 사용하였다는 것 입니다. "$\dot{q}$ = p인데, $\dot{q}$를 이용하여 전개한 것이나 $p$를 이용하여 전개한 것이나 같은 것이 아니냐?" 라고 할 수 도 있습니다. 맞긴 한데, 그렇다고 해서 두 표현법이 완전히 같은 것은 또 아닙니다.
에너지 보존 법칙은 해밀토니안 행렬 $H$가 시간에 무관한 값이 되어야 함을 의미하는데, 앞서 설명한 바와 같이 어떤 행렬의 시간에 따른 미분이 0이 되면 그 행렬은 대각 행렬이어야 합니다. 즉, 해밀토니안 행렬을 대각 행렬이 되어야 하고, 대각 행렬이 경우에는 일반적인 엇대각 성분값이 0이 아닌 행렬과는 다르게, 행렬의 대각 성분의 값을 익숙한 물리량으로 해석할 수 있습니다. 만일 해밀토니안 행렬의 대각성분 $H(nn)$을 양자 상태 $n$의 에너지로 이해한다면, 보어의 주기 조건에 의해서 $$hv(nm) = H(nn) - H(mm)$$ 이 되어야 합니다. 보른과 요르당의 논문에서는 이 부분이 다음과 같이 설명 돼 있습니다.
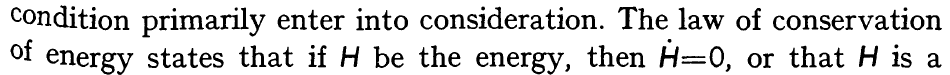

이 다음 부분은 이 논문에서 가장 핵심적인 부분이자, 최초로 $[\hat{x}, \hat{p}] = i \hbar I$ 가 등장하는 부분입니다. $[\hat{x}, \hat{p}] = i \hbar I$의 유도는 어떻게 생각하면 생각 보다 조금 싱겁기도 합니다.

$d = pq - qp$ 를 정의 합니다. 행렬 $d$를 미분하고, 해밀토니안 운동 방정식에서 부터 $\dot{p}, \dot{q}$를 $-\frac{\partial H}{\partial q}, \frac{\partial H}{\partial p}$로 대입하면 위와 같은 식을 얻습니다.

위와 같은 형태의 식은 이미 앞에서 한 번 등장한 바 있는데, 행렬 $z$가 $p, q$의 다항식으로 주어지는 경우,
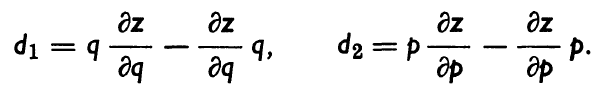
에 대해서

가 항상 성립하게 됩니다. 따라서 $d = pq - qp$는 시간에 무관한 행렬이 되고, 시간에 무관한 행렬은 대각행렬이 되어야 합니다. $pq - qp$의 대각 성분은 식 (37)과 같이 주어지게 되고, 이를 모두 정리하여 하나의 수식으로 표현하면, 식 (38)을 얻게 됩니다! 보른과 요르당은 이 식을 "강한 양자화 조건"이라고 명명하였고, (논문의 이후) 모든 결과가 이 식으로 부터 얻어진다(유도된다)를 밝혔습니다. 하이젠베르크의 양자화 조건은 $pq-qp$의 대각 성분에 대한 조건이지만, 보른-요르당의 양자화 조건은 대각 성분의 조건뿐 아니라 엇대각 성분의 조건을 모두 포함하기 때문에 "강한" 이라는 단어를 추가한 것 같습니다. 하이젠베르크가 양자화 조건의 일부(대각성분만)를 밝혀냈다면, 보른과 요르당은 나머지 부분(엇대각성분)의 조건을 밝혀냈을 뿐 아니라, 이를 수학적으로 완벽하게 기술하였습니다.
행렬 $p, q$의 교환법칙을 알아 냈으니, $p, q$와 관련된 식의 전개를 보다 쉽게 할 수 있습니다. 예를들면,

와 같은 전개 입니다. $pq - qp = \frac{h}{2 \pi i}I$ 를 여러번 사용하여 식을 간단히 표현하면 식 (39)를 얻을 수 있습니다. 학부 양자역학 수업시간에 자주 하는 계산법이니 양자역학을 배우신 분이라면 쉽게 유도할 수 있는 식 입니다.
위 계산 방법을 활용하면 해밀토니안과 $p, q$ 행렬과의 교환 관계를 계산할 수 있습니다. 보른과 요르당 역시 이에 대해서 논의를 계속 합니다.

해밀토니안이 $p$의 다항함수와 $q$의 다항함수의 합으로 이뤄져 있다면, 간단한 문제의 경우 그렇게 됩니다, 식(40)를 얻을 수 있고, 이로 부터 $p, q$의 시간에 따른 미분, 즉 운동 방정식은 식 (41)과 같이 얻어짐을 유도할 수 있습니다. $p, q$의 함수로 주어지는 일반적인 물리량과 관련된 행렬의 경우

식 (43)과 같이 운동 방정식이 주어집니다.
위 식 (43)을 현대적인 표기법으로 쓰면,
$$i \hbar \frac{d}{dt}g = [g, H]$$
입니다. 이 식은 양자역학 교과서에서 많이 보셨을 것 입니다.
(3) Investigation of the anharmonic oscillator
이번 챕터에서는 물리 문제에서 가장 단순하면서도 가장 중요한 문제인 단조화 진동자 문제에 "강한 양자화 조건"을 부여하여 양자역학적인 단조화 진동자 문제를 풉니다. 보른과 요르당은 "하이젠베르크가 이미 단조화 진동자 문제를 풀었지만, 자신들은 보다 일반적인 방법으로 문제를 푼다"를 강조합니다.

단조화 진동자의 운동방정식 (54)의 $q$에 행렬을 대입하면, 각 성분별로 식 (55)를 만족시켜야 합니다. 모든 $(nm)$에 대해서 식 (55)가 성립하기 위해서는 당연히 $q(nm)=0$ 이거나 $v^2(nm) - v_0^2 = 0$ 이면 입니다. 특정한 $n$에서,모든 $m$에서 $q(nm) = 0$이 되어서는 안되기 때문에 (만일 그렇게 된다면 행렬 $q$의 $n$ 번째 열과 행이 제로 벡터가 되고, 식 (56)의 강한 양자화 조건을 만족하지 않게 됩니다), 적어도 하나 이상의 $m$에서는 $v^2(nm) - v_0^2 = 0$이 성립해야 합니다. 각 $n$에 대해서 $v^2(nm) - v_0^2 = 0$을 만족하는 $m$을 $n'$이라고 한다면, $|W_n - W_n'| = hv_0$를 얻게 되고, 에너지 준위의 차이가 $hv_0$로 주어짐을 얻게 됩니다. 또한 $n$을 기준으로 에너지가 더 크거나 더 작은 에너지 준위가 각각 존재함을 알 수 있고, 이를 $n', n''$ 이라고 놓을 수 있습니다.
이 결과를 $q, p$ 행렬에 적용하고 해밀토니안 행렬을 구하면,

가 됩니다. 식 $H(nm)$과 특별히 대각성분은 식 (59)의 결론에 도달할 수 있습니다. 이 과정에서 $v(nm) = -v(mn)$을 이용하였습니다.
식 (56)은 강한 양자화 조건의 대각성분의 값을 이용해서 바로 구해지는 식 입니다. $pq - qp$의 대각 성분 $(nn)$ 성분을 생각하면, $$\frac{h}{2 \pi i} = \vec{p}_n^* \cdot \vec{q}_n - \vec{q}_n^* \cdot \vec{p}_n$$ 가 되고, 여기서 $p = i 2 \pi v q$ 와 행렬 $p, q$가 hermitian 행렬이라는 조건($p(nm) = p(mn)^*$)을 이용하면 식 (56)을 얻을 수 있습니다.

앞에서 임의의 $n$에 대해서 에너지 차이가 $hv_0$가 나는 최대 두 상태 $n', n''$가 존재할 수 있음을 얻었습니다. 만일 둘 중에 하나의 상태만 가능하고($n''$ 상태가 존재하지 않고), $n'$ 상태의 에너지가 $n$ 상태의 에너지 보다 크다고 하면, 상태 $n$의 에너지는 $\frac{1}{2} h_0$ 를 얻습니다. 이 상태 보다 에너지가 낮은 에너지 상태가 존재 하지 않기 때문에, 이 상태가 바닥 상태가 되는 것이고, 이때의 에너지가 바로 $\frac{1}{2} h_0$가 됩니다! 단조화 진동자 문제를 풀 때 익히 봐 왔던 바닥 상태에 대한 에너지 공식 입입니다.
임의의 경우에 대해서는

의 결론을 얻을 수 있습니다. 이는 일반적인 단조화 진동자의 에너지 고유값이 됩니다. 학부 양자역학 시간에 단조화 진동자 문제를 풀 때는 생성/소멸 연산자를 도입하고, 해밀토니안을 생성/소멸 연산자의 곱으로 표현한 뒤, 간단한 대수적인 방법을 통해서 얻은 에너지 고유값 $E_n = hv_0(n + \frac{1}{2})$와 일치하는 결론 입니다. 보른과 요르당이 푼 방식이 조금은 더 복잡하긴 하지만 운동 방정식과 강한 양자화 조건을 직접적으로 활용하여 에너지 고유값을 얻은 과정이라고 볼 수 있습니다.
보른과 요르당은 좀 더 일반적인 $\frac{1}{3}\lambda q^3$ 항이 추가된 비조화 진동자 문제를 풉니다. $\lambda$에 대한 섭동 전개를 이용하여 에너지 고유값을 계산하는데, 이는 복잡하기도 하고 당장은 그렇게까지 의미 있는 내용은 아니라서 이를 설명하는 것은 생략하기로 합니다.
요약
보른과 요르당은 하이젠베르크가 창안한 새로운 형태의 역학에 "행렬"이라는 언어를 도입하여 수학적으로 체계적인 이론에 도달하였습니다. 이는 그들이 "강한 양자화 조건"이라고 명명한 $pq - qp = \frac{h}{2 \pi i}I$로 요약됩니다. 하이젠베르크가 무(無)에서 유(有)를 창조했다면, 보른과 요르당은 작은 유를 매우 큰 유로 만들었습니다.
학부 양자역학에서는 보통 하이젠베르크, 슈뢰딩거의 이름은 쉽게 접할 수 있지만, 보른과 요르당의 이름은 좀 처럼 접하기 어렵습니다. 보른은 파동함수의 확률적 해석이라는 업적을 통해서 접하게 되지만 요르당의 이름은 거의 접할 기회가 없습니다. (이는 요르당의 정치적인 행보 때문이기도 한데, 디테일한 설명은 생략하도록 하겠습니다) 비록 두 사람의 업적이 양자역학 교과서 수준에서는 설명되지 않는 것이 사실이지만, 이 둘은 초기 양자역학의 탄생에 지대한 공헌을 했음은 틀림 없습니다.
'물리학' 카테고리의 다른 글
| 수소 원자의 선 스펙트럼 문제를 행렬 역학의 방법으로 풀어낸 볼프강 파울리 (0) | 2022.03.16 |
|---|---|
| 폴 디랙에 의한 정준 양자화(Canonical Quantization)의 탄생 (0) | 2022.03.15 |
| 하이젠베르크는 어떻게 행렬역학을 유도하였나? (양자역학이 시작된 하이젠베르크의 1925년 논문 이해하기) (1) | 2022.03.08 |
| 투사체 궤적의 포락선(envelope function) 구하기 (0) | 2022.02.11 |
| 곡선 위를 따라 움직이는 입자의 운동 방정식 (3) | 2021.11.21 |


