
이번 포스팅에서는 위 그림에서와 같이 곡선 위를 따라 움직이는 입자의 운동 방정식을 어떻게 구할 수 있고, 운동 방정식을 수치적인 방법을 통해서 실제로 푸는 방법에 대해서 알아 보도록 하겠습니다.
곡선의 매개 변수화
일반적으로 곡선은
$$\vec{r}(\theta) : \theta \in [a,b] \in \mathbb{R} \rightarrow \vec{r} = (x_1, x_2, ..., x_N) \in \mathbb{R}^N$$
으로 표현할 수 있습니다. 우리 문제의 경우, 실제 공간은 3차원 이지만 문제를 좀 더 쉽게 하기 위해서 공간을 2차원으로 제한 하도록 하겠습니다. 따라서, 곡선을 기술하는 매개 변수를 $\theta$라고 할 때, $(x(\theta), y(\theta))$로 나타낼 수 있습니다. 그리고 배개 변수 $\theta$의 범위는 $[\theta_1, \theta_2]$로 하겠습니다.

위 식을 그림으로 나타내면 위와 같습니다. 편의상, 왼쪽 위의 점을 곡선의 시작, 오른쪽 아래의 점을 곡선의 끝으로 하였습니다. $\theta$가 커질 수록 왼쪽 위 점에서 오른쪽 아래의 점으로 이동하게 됩니다. 물론 $\theta$는 단순히 곡선을 기술하기 위해서 도입된 매개 변수로, 시간 $t$는 아닙니다.
실제로 곡선 위를 움직이는 입자(하늘색으로 표시)의 시간 $t$에 따른 좌표는 $(x(t), y(t))$로 기술이 되는데, $(x, y)$가 모두 $\theta$로 기술이 되기 때문에, 자연스럽게 $x(t) = x(\theta(t)), y(t) = y(\theta(t))$와 같이 표현할 수 있습니다. 즉 입자의 시간에 따른 위치 변화는 입자의 위치를 기술하는 매개 변수 $\theta$의 시간에 따른 변화가 됩니다.
운동 방정식
입자의 움직임을 기술하기 위해서는 뉴턴의 운동 방정식을 세우면 됩니다.

위 그림은 곡선 위에 입자가 있는 곳을 확대한 모습입니다. 입자는 곡선 상에 존재하지만, 국소적으로 보면 녹색 삼각형으로 그린 것과 같이 빗면 위에 있다고 볼 수 있습니다. 따라서 매우 짧은 시간, 매우 짧은 거리 동안에는 입자는 곡선이 아닌 직선 상의 운동을 하게 되고, 입자의 운동 방정식은 빗면 위를 움직이는 입자의 운동 방정식이 됩니다.

빗면에서 입자의 움직임은 물리학을 처음 배우는 고등학교 시절에 배우게 됩니다. 빗면에 입자가 놓여 있으면 거의 본능적으로 위 그림과 같이 중력(노란색으로 표시)를 빗면 방향의 힘(붉은색으로 표시)과 빗면에 수직한 힘(연두색으로 표시)으로 분해하게 됩니다. 빗면의 기울기 각도를 $\phi$라고 할 때, 빗면 방향으로 가해지는 힘의 크기는 빗면에서 내려 가는 방향으로 $mg \sin (\phi)$가 됩니다. 빗면의 한 기준점에서 입자가 내려간 거리를 $s$라고 한다면, 운동 방정식은
$$\frac{d^2s}{dt^2} = mg \sin (\phi)$$
가 됩니다.

입자가 놓여 있는 지점을 국소적인 빗면의 시작이라고 한다면, 빗면의 크기(길이)는 위 그림과 같이 면적소 $dx, dy, ds =\sqrt{dx^2 + dy^2}$를 이용하여 나타낼 수 있습니다. 또한 $\sin (\phi) = \frac{dy}{ds} = \frac{dy}{\sqrt{dx^2 + dy^2}}$ 가 됩니다. $x, y$가 모두 $\theta$의 함수이기 때문에,
$$dx = \frac{dx}{d\theta} d\theta = x_{\theta} d \theta$$
$$dy = \frac{dy}{d\theta} d\theta = y_{\theta} d \theta$$
$$ds = \sqrt{\Big(\frac{dx}{d\theta}\Big)^2 + \Big(\frac{dy}{d\theta}\Big)^2} d\theta = \sqrt{x_{\theta}^2 + y_{\theta}^2} d\theta$$
로 표현할 수 있습니다.
이로 부터,
$$\frac{ds}{dt} = \sqrt{x_{\theta}^2 + y_{\theta}^2} \frac{d\theta}{dt} = \sqrt{x_{\theta}^2 + y_{\theta}^2} \dot{\theta}$$
를 얻습니다. 그냥 간단히 Chain rule를 사용하여
$$\frac{ds}{dt} = \sqrt{\Big(\frac{dx}{dt}\Big)^2 + \Big(\frac{dy}{dt}\Big)^2} = \sqrt{\Big(\frac{dx}{d\theta}\frac{d\theta}{dt}\Big)^2 + \Big(\frac{dy}{d\theta}\frac{d\theta}{dt}\Big)^2} = \sqrt{x_{\theta}^2 + y_{\theta}^2} \dot{\theta}$$
와 같이 $\frac{ds}{dt}$를 구할 수 도 있습니다.
한 번 더 시간에 대해서 미분 하게 되면,
$$\frac{d^2s}{dt^2} = \sqrt{x_{\theta}^2 + y_{\theta}^2} \ddot{\theta} + \dot{\theta} \frac{d}{dt}\Big( \sqrt{x_{\theta}^2 + y_{\theta}^2}\Big)$$
$$ = \sqrt{x_{\theta}^2 + y_{\theta}^2} \ddot{\theta} + \frac{\Big(x_{\theta} x_{\theta\theta} + y_{\theta} y_{\theta\theta}\Big)}{\sqrt{x_{\theta}^2 + y_{\theta}^2}} \dot{\theta}^2 $$
가 됩니다. 특별히 어려운 과정은 없고, 여러번 Chain rule를 사용하면 됩니다.
이제 중력에 해당하는 항 $\sin (\phi) = \frac{dy}{ds} = \frac{dy}{\sqrt{dx^2 + dy^2}}$을 $\theta$에 대한 식으로 쓰겠습니다. 역시나 Chain rule를 쓰면 되는데,
$$\frac{dy}{ds} = \frac{dy}{d\theta}\frac{d\theta}{ds} = \frac{\frac{dy}{d\theta}}{\frac{ds}{d\theta}} = \frac{y_{\theta}}{\sqrt{x_{\theta}^2 + y_{\theta}^2}}$$가 됩니다.
최종적인 운동 방정식은
$$\sqrt{x_{\theta}^2 + y_{\theta}^2} \ddot{\theta} + \frac{\Big(x_{\theta} x_{\theta\theta} + y_{\theta} y_{\theta\theta}\Big)}{\sqrt{x_{\theta}^2 + y_{\theta}^2}} \dot{\theta}^2 = - \frac{y_{\theta}}{\sqrt{x_{\theta}^2 + y_{\theta}^2}}$$
입니다. 여기서 우항에 마이너스 부호가 붙는 것은, 위 그림에서도 볼 수 있듯 $\frac{dy}{d\theta}$가 음수인 경우에 $s$의 방향으로 힘이 작용하기 때문입니다. $\ddot{\theta}$의 계수를 1로 만들어 주기 위해서 양변을 $\sqrt{x_{\theta}^2 + y_{\theta}^2}$로 나누어 주고, 우변을 좌변으로 넘기면,
$$\ddot{\theta} + \frac{\Big(x_{\theta} x_{\theta\theta} + y_{\theta} y_{\theta\theta}\Big)}{x_{\theta}^2 + y_{\theta}^2} \dot{\theta}^2 +\frac{y_{\theta}}{x_{\theta}^2 + y_{\theta}^2} = 0$$
이 우리가 구하려는 최종적인 운동 방정식이 됩니다. 곡선의 매개 변수 $\theta$가 입자의 위치를 기술하는 변수이기 때문에 결과적으로 $\theta$에 대한 2계 미분 방정식이 얻어진 것 입니다. 위 방정식에 초기 조건을 대입하려 풀어서 $\theta(t)$를 얻으면 이로 부터 최종적으로 얻어야 하는 식인 $x(t) = x(\theta(t)), y(t) = y(\theta(t))$를 얻게 됩니다.
특수한 매개 변수에 대한 운동 방정식
앞에서 설명한 것과 같이 2차원 평면에서 곡선은 매개변수 $\theta$를 이용하여 $(x(\theta), y(\theta))$로 기술이 가능합니다. 이 중에서 만일 $\theta =x $ 인 경우의 곡선은 $(x, y(x))$가 되는데, 이 곡선은 그래프 $y = y(x)$입니다. 이로 부터 $x(t)$의 운동 방정식
$$\frac{d^2x}{dt^2} + \frac{y_x y_{xx}}{1 + y_x^2} \Big(\frac{dx}{dt} \Big)^2 + g\frac{y_x}{1 + y_{xx}^2} = 0$$
가 됩니다. $x(t)$를 얻은 후에, $y = y(x)$로 부터 $y(t)$를 바로 얻을 수 있습니다.
실제 문제를 풀어 보자
운동 방정식은 2계 미분 방정식이고, 이전 포스팅에서 많이 다뤘던 오일러 방법이나 룽게-쿠타 방법을 통해서 수치적인 해를 구할 수 있습니다. 예시로 $y(x) = \frac{1}{5}(x-2)^2 + \cos(\pi x)$ 그래프를 따라서 낙하하는 물체의 궤적을 구해보도로 하겠습니다.

$y(x) = \frac{1}{5}(x-2)^2 + \cos(\pi x)$는 위와 같은 개형입니다. 초기 조건 $x=0.3, \frac{dx}{dt}(0) = 0$에 해당하는 입자의 시간에 따른 궤적은 다음 동영상과 같습니다.
https://www.youtube.com/watch?v=MMKklYQYxpw
일상적인 경험에서 보는 것과 같은 형태의 $(x(t), y(t))$가 얻어졌습니다. 위 미분 방정식에서는 공기의 저항이나 마찰력은 전혀 고려하지 않았고, 단순히 중력에 의한 운동만 고려하였기 때문에 $x=0.3$에서 놓여진 입자는 반대편 $x=4-0.3 = 3.7$까지 올라 간 뒤, 다시 뒤로 돌아 오는 운동을 반복하게 됩니다.
사이클로이드의 경우
사이클로이드 곡선 상을 움직이는 입자의 시간에 따른 위치를 계산해 보겠습니다. 사이클로이드 곡선의 매개 변수화는
$$x(\theta) = r(\theta - \sin (\theta)) -\pi r$$
$$y(\theta) = -r (1 - \cos (\theta) ) + 2r$$
입니다. 여기서 $\theta \in [0, 2\pi]$ 이고, $r$은 사이클로이드의 "크기"를 기술하는 파라미터입니다. 앞으로 계산의 편의상 $r=1$로 고정하도록 하겠습니다. 이 블로그에서 여러번 다뤄 본 것과 같이 사이클로이드는 등시곡선으로 어느 위치에서 초기 운동을 하든 상관 없이 한 주기 운동의 주기는 $T = 4 \pi$ 로 일정합니다.
https://www.youtube.com/watch?v=j3gOryXjxvY
서로 다른 4개의 초기 위치에 대한 주기 운동의 결과는 위 영상과 같습니다. 해석적으로도 증명할 수 있는 것과 같이 초기 높이와는 상관 없이 주기 운동의 주기는 일정함을 수치적인 방법을 통해서도 확인할 수 있습니다.
마찰력을 추가하자
좀 더 현실적인 시뮬레이션을 위해서는 마찰력을 추가해야 합니다. 간단한 모델에 따르면, 마찰력은 수직항력과 마찰 계수의 곱에 비례합니다. 수직항력은 위 힘 분해 그림에서 $mg \cos (\phi)$가 되고, 마찰 계수를 $\mu$라고 하면 마찰력은 $F = \mu mg \cos (\phi)$가 됩니다. 위에서 $\sin (\phi)$를 $\theta$의 함수로 표현한 것과 같이 $\sin (\phi)$를 $\theta$의 함수로 표현하면, $F = -\mu \frac{x_{\theta}}{\sqrt{x_{\theta}^2 + y_{\theta}^2}}$
이 됩니다. 여기서 $F$는 마찰력의 크기만을 나타낸 것으로, 마찰력의 방향을 추가해 주어야 하는데요, 마찰력의 방향은 속력 $\frac{ds}{dt}$의 반대 방향이 되는데, $\frac{ds}{dt} = \sqrt{x_{\theta}^2 + y_{\theta}^2} \dot{\theta}$이므로, 속력의 반대방향은 곧 $\dot{\theta}$의 반대 방향이 됩니다. 이로부터 속력의 반대 방향은 $\frac{\dot{\theta}}{|\dot{\theta}|}$가 되고, 바닥과 물체와의 마찰을 고려한 $\theta$의 운동 방정식은 최종적으로,
$$\ddot{\theta} + \frac{\Big(x_{\theta} x_{\theta\theta} + y_{\theta} y_{\theta\theta}\Big)}{x_{\theta}^2 + y_{\theta}^2} \dot{\theta}^2 +\frac{y_{\theta}}{x_{\theta}^2 + y_{\theta}^2} -\mu \frac{x_{\theta}}{x_{\theta}^2 + y_{\theta}^2} \frac{\dot{\theta}}{|\dot{\theta}|}= 0$$
이 됩니다.
프로그래밍 코드에도 마지막 항을 추가한 뒤 시뮬레이션을 할 수 있습니다.
https://www.youtube.com/watch?v=5dOKHdtpCh8
결과는 위 영상과 같습니다. 입자는 초기 높이 $2$에서 운동을 시작했습니다. 마찰력이 없다면 반대편 가장 높은 곳까지 올라가겠지만 바닥과의 마찰로 인해 역학적 에너지가 손실되기 때문에 입자는 반대편 꼭대기 까지 올라가지 못 합니다. 진폭은 계속해서 줄어들게 되고, 최종적으로는 멈추게 됩니다. 사이클로이드의 가장 낮은 곳에서 멈추는 것이 아니라, 저항 때문에 중심에서 약간 떨어진 곳에서 멈추게 됩니다.
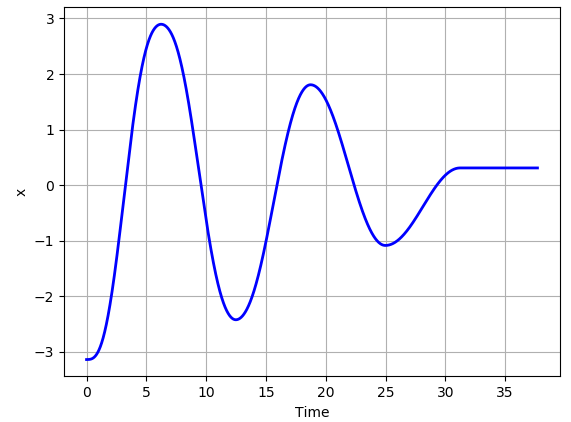
시간에 따른 입자의 $x$축 좌표를 그래프로 그리면 위와 같습니다. 앞서 언급한바와 같이 초기 위치는 높이가 $2$인 곳인데, 이 곳의 $x$좌표는 $-\pi$입니다. 이 시뮬레이션의 물리 상수 세팅에서는 2번 왕복 운동을 한 뒤, 최저점 근처에서 멈춰지게 됩니다.
속도에 비례하는 공기 저항을 추가하자
물체에 작용하는 힘은 중력, 바닥과의 마찰력 외에도 공기와의 저항력이 있습니다. 공기 저항에도 다양한 모델이 있지만, 그 중에서 가장 간단한 속도에 비례하는 공기 저항을 생각해 보도록 하겠습니다. 입자의 속력(속도의 크기)는 $\frac{ds}{dt} = \sqrt{x_{\theta}^2 + y_{\theta}^2} \cdot {\theta}$ 이고 공기 저항의 비례 상수를 $k$라고 한다면, 공기 정항에 의한 힘은 최종적으로 $F =-k \sqrt{x_{\theta}^2 + y_{\theta}^2} \cdot {\theta}$가 됩니다. 앞에 붙는 부호 $-$는 속도의 방향과 공기 저항의 방향이 반대라는 의미 입니다. 이 항을 $\theta$의 운동 방정식에 추가하면 됩니다.
'물리학' 카테고리의 다른 글
| 하이젠베르크는 어떻게 행렬역학을 유도하였나? (양자역학이 시작된 하이젠베르크의 1925년 논문 이해하기) (1) | 2022.03.08 |
|---|---|
| 투사체 궤적의 포락선(envelope function) 구하기 (0) | 2022.02.11 |
| 그린함수에 대한 설명과 감쇄 조화 진동자 문제에 적용(Green's function and its application to damped harmonic oscillator) (0) | 2021.11.08 |
| 1차원 공간에서 슈뢰딩거 방정식에 대한 몇 가지 정리 (0) | 2021.10.30 |
| 몬테 카를로 시뮬레이션을 이용하여 통계 역학의 문제 풀기 (1) : 토이 모델 예시 (0) | 2021.10.24 |


