고전 역학 (Classical Mechanics)
고전 역학은 물체에 작용하는 힘과 이에 대한 물체의 반응이라 할 수 있는 물체의 운동(움직임)과의 관계를 설명하는 물리학의 한 분야 입니다. 고전 역학은 물리학 뿐 아니라 모든 과학의 분과 중에서 가장 먼저 탄생한 분야이며, 수학을 이용하여 자연 현상을 기술할 뿐 아니라, 현상의 기저에 있는 원리를 밝혀내는 학문입니다. 일반인들에게 있어 가장 친숙한 물리학의 분야임과 동시에, 중고등학교 교과과정에서도 처음 접할 수 있는 분야입니다.
뉴턴 역학 (Newton(ian) Mechanics)
고전 역학은 뉴턴 역학이라는 이름으로 불리기도 하는데, 물체의 운동 법칙을 발견한 물리학자이자 수학자인 아이작 뉴턴의 이름을 딴 것 입니다. 중고등학교 시절 물리를 포기하신 분들도 뉴턴의 이름을 들어보셨을 것 입니다. 뉴턴은 유명한 세 가지 운동 법칙을 통해서, 사과가 중력으로 인해 낙하하는 것 부터 하늘에 떠 있는 행성의 움직임까지 세상의 "삼라만상"을 수학적으로 정교하게 기술하였습니다.
뉴턴 역학의 체계를 이루는 여러 개념과 방정식 중에서, 가장 중요한 개념은 힘, 질량, 가속도이며, 이들 힘, 질량, 가속도의 관계식을 설명하는 것이 뉴턴의 운동 법칙 중 제 2법칙이라고 불리는 힘-가속도 법칙,
$$\vec{a} = \frac{d^2x}{dt^2} = \frac{1}{m}\vec{F}$$
입니다. 이 벡터 미분 방정식을 통해서 힘이 작용하는 물체의 시간에 따른 움직임을 정확하게 계산할 수 있습니다. 실제로 물체에 작용하는 모든 힘을 구하고, 이로 부터 물체의 움직임을 매우 정확하게 묘사하는 것은 계산의 복잡성으로 인해 어렵지만, 적어도 원리적으로 볼 때, 이 방정식은 일상의 영역의 "거의 모든"것을 설명한다고 볼 수 있습니다. 흔히 정역학이라고 불리기도 하는 움직이지 않는 물체에 대학 역학 역시 뉴턴의 운동 법칙으로 설명이 가능한데, 이를 통해서 물체에 작용하고 있는 힘, 압력 등을 구할 수 있습니다.
라그랑주 역학 (Lagrangian Mechanics)
라그랑주 역학은 뉴턴 역학과는 조금 다른 개념과 방식으로 시간에 따른 물체의 움직임을 기술하는 방법입니다. 뉴턴 역학에서 가장 중요한 개념이 힘, 질량, 가속도였다면 라그랑주 역학에서 가장 중요한 개념은 라그랑지안과 일반화 좌표 입니다. 뉴턴 역학에서 $\vec{F} = m\vec{a}$ 의 식을 통해 시간에 따른 물체의 움직임을 설명했다면, 라그랑주 역학에서는 라그랑지안과 오일러-라그랑주 방정식을 통해서 역학 시스템을 설명합니다.
$$\frac{\partial L}{\partial q} + \frac{d}{dt} \big( \frac{\partial L}{\partial \dot{q}}\big) = 0 $$
뉴턴의 방법으로 시간에 다른 물체의 움직임을 계산하는 것이나, 라그랑주의 방법으로 시간에 따른 물체의 움직임을 계산하는 것이나 둘은 같은 결과를 줍니다. 당연하게도, 한 가지 자연 현상을 설명하는 것이니 둘의 답은 같아야 합니다. "서로 같은 답을 주는 것인데 왜 방법이 두 가지나 필요한가?" 라고 의문을 가지실 수 도 있는데, 이 의문에 대한 답이 라그랑주 역학의 존재의 이유라고 할 수 있습니다.
라그랑주 역학이 필요한 이유는 라그랑주의 방법론은 때에 따라서 뉴턴의 방법 보다 훨씬 더 쉬운 과정을 통해서 최종 답을 얻을 수 있기 때문입니다. 이를 이해하려면 여러 문장이나 그림을 통해서 설명하는 것 보다는 실제로 문제를 풀어 보는게 가장 좋은데, 꼭 이 블로그가 아니더라도 웹 상의 많은 페이지에서 이와 관련된 설명을 하고 있기에 이 글에서는 생략을 하겠습니다.
뉴턴 역학과 비교될 수 있는 라그랑주 역학의 특징을 요약하면
(1) 뉴턴 역학이 물체의 움직임을 물체에 작용하는 힘에 대한 응답으로 생각했다면, 라그랑주 역학에서의 물체의 움직임은 라그랑지 함수로 부터 정의된 시스템의 "액션"을 최소화 하는 경로를 따른다
(2) 물체의 시간에 다른 움직임은 벡터 미분 방정식이 아닌 스칼라 미분 방정식으로 주어진다
(3) 물체의 위치를 기술 할 수 있는 임의의 좌표를 사용하여 방정식을 세울 수 있다
(4) 동일한 방법론을 고전 역학 뿐 아니라, 전자기학, 양자역학 등에 적용할 수 있다
입니다. 위 하나 하나에 대한 설명을 하기 위해서도 많은 분량이 필요한데, 위 토픽은 이 포스팅의 주제가 아니기 때문에 생략하도록 하겠습니다.
해밀턴 역학 (Hamilton Mechanics)
해밀턴 역학은 뉴턴 역학, 라그랑주 역학과 또 다른 방식으로 시간에 따른 물체의 움직임을 기술하는 방법입니다. 해밀턴 역학에서 물체의 움직임을 기술하는 방정식은 해밀턴 운동 방정식으로 라그랑주 방정식과 비교할 때, 라그랑주 방정식은 물체의 위치를 기술하는 일반화 좌표의 2계 미분 방정식인 반면, 해밀턴 방정식은 일반화 좌표와 이것의 일반화 운동량에 대한 1계 미분 방정식입니다. 즉, (각 자유도에 대해서) 1변수 2계 미분 방정식이 2변수 1계 미분 방정식으로 바뀐 것 입니다.
해밀턴 역학에서는 위치와 운동량을 서로 독립적이면서 대등한 변수로 생각하고, 위치와 운동량이 정의되는 위상 공간에서 위치와 운동량이 시간에 따라서 어떻게 변화하는지를 계산합니다. 위상 공간에서 위치와 운동량 $(q_i, p_i)$의 시간에 따른 변화는 해밀턴 운동 방정식 혹은 정준 방정식(canonical equation) 이라고 불리는,
$$\frac{dq_i}{dt} = \frac{\partial H}{\partial p_i}, \frac{dp_i}{dt} = -\frac{\partial H}{\partial q_i}$$
에 의해 결정 됩니다. 여기서 $H$는 해밀토니안으로 시스템이 위상 공간에서 어떻게 변화하는지를 결정하는 함수 입니다. 가장 간단한, 시간에 무관하면서 보존장에 지배를 받은 시스템을 생각하면, $H(q_i, p_i) = \frac{p_i^2}{2m} + V(q_i)$ 가 됩니다. 여기서 $V(q_i)$ 는 시스템의 위치 에너지 입니다.
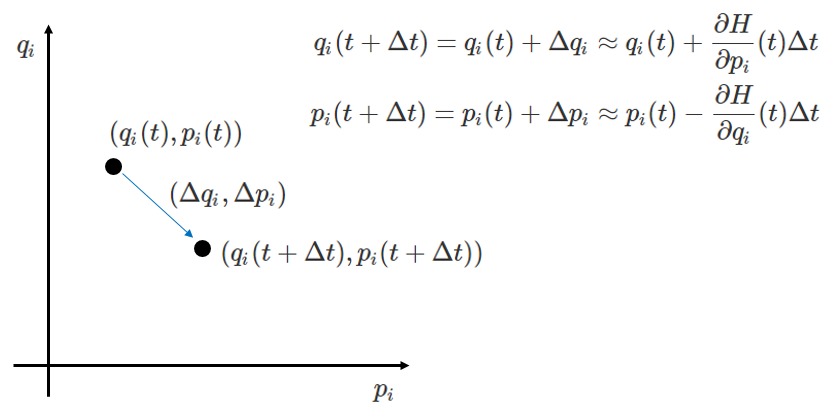
위에서 설명한 과정을 그림으로 표현하면 위와 같습니다.
시간 $t=t$에서 시스템이 위상 공간의 점 $(q_i(t), p_i(t))$에 있었다면, $\Delta t$ 이후 이 시스템의 위상 공간에서의 위치 $(q_i(t + \Delta t), p_i(t + \Delta t))$ 는 $(q_i(t), p_i(t))$에서 $(\Delta q_i, \Delta p_i)$ 만큼 이동하게 되는데, $\Delta q_i, \Delta p_i$는 각각 $\frac{\partial H}{\partial p_i} \Delta t, -\frac{\partial H}{\partial q_i} \Delta t$가 됩니다. 이처럼 해밀턴 방정식은 2변수에 대한 1계 미분 방정식이기 때문에, 미분 방정식의 해를 개념적으로 이해하기가 더 쉽습니다. 물론 변수이 갯수가 1개 $(q_i(t))$에서 2개 $(q_i(t), p_i(t))$로 늘었다는 단점이 있습니다.
해밀턴 역학으로 푸는 단조화 진동자
가장 쉬운 물리 시스템이라 할 수 있는 1차원 단조화 진동자 (SHO : Simple Harmonic Oscillator) 문제를 해밀턴 역학의 방법으로 풀어 보도록 하겠습니다. 질량이 $m$ 인 물체가 용수철 상수가 $k = m\omega^2$ 인 용수철에 매달려 진동하는 시스템입니다. 너무 유명한 시스템이라서 이 시스템에 대한 더 이상의 설명은 필요 없을 듯 합니다.
우선, 시스템의 해밀토니안을 구해야 합니다. 이 시스템은 시간에 무관한 시스템이며 위치 에너지가 $V = \frac{1}{2}kx^2 = \frac{1}{2}m\omega^2 x^2$ 으로 주어지기 때문에 해밀토니안 H는 $H = \frac{p^2}{2m} + \frac{1}{2}m\omega^2 x^2$ 이 됩니다. 계산의 편의를 위해서 $m=1, \omega = 1$ 로 가정 하면, $H = \frac{1}{2}p^2 + \frac{1}{2}x^2$ 이 됩니다. 위 과정은 $p' = \frac{p}{\sqrt{m}}, x' = \sqrt{m}\omega x$ 와 같은 좌표 변환을 정의하여 $H(x',p') = \frac{1}{2}p'^2 + \frac{1}{2}x'^2$ 을 정의했다고 생각해도 됩니다. 이 시스템의 정준 방정식은 정의에 따라서,
$$\dot{x} = p , \dot{p} = -x$$
이 됩니다. 이 연립 미분 방정식의 일반해는 $(x(t), p(t)) = (A \sin(t + t_0), A \cos(t + t_0))$ 가 됨을 쉽게 확인 할 수 있습니다. 여기서 $A, t_0$는 초기 조건 (구속 조건)에 의해서 정해지는 값 입니다.
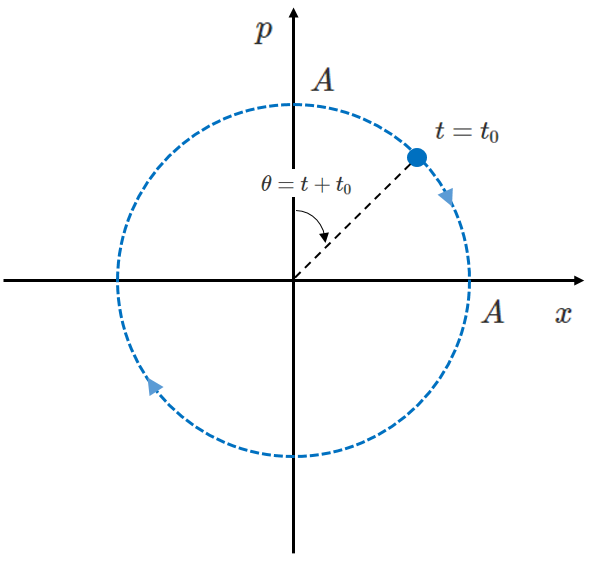
$(x(t), p(t)) = (A \sin(t+t_0), A \cos(t+t_0))$ 의 자취를 위상 공간에서 표현하면 위와 같습니다. $t+ t_0$ 는 일종의 "각도" 역할을 하는데 $p$ 축과의 각도를 의미 합니다. 시간이 흐름에 따라서 위 점은 시계 방향으로 반름이 $A$인 원을 그리며 회전하게 됩니다.
그래서 뭐 어쩌라고?
해밀턴 역학에 대한 설명을 여기까지만 하면 "뭐 어쩌라고?" 라는 질문이 반드시 나올 것 입니다. 라그랑주 방정식의 경우, 매우 복잡한 시스템에 대한 운동 방정식을 쉽게 얻게 해 준다는 장점이 분명하고, 특히 구족 조건이 있스 시스템에서 일반화 좌표를 이용하면 운동 방정식이 뉴턴 역학을 통해서 얻을 때 보다 훨씬 더 쉽게 얻어짐을 경험하였을 것 입니다.
그러나 위 예제에서는 "굳이 이런 방식으로 문제를 풀 필요가 있나?"하는 의문이 생깁니다. 최종적으로 얻어지는 미분 방정식은 뉴턴의 방법이나 라그랑주의 방법으로 구했을 때랑 (당연히) 똑같고, 그 과정이 쉬워지거나 개념적으로 쉬워지거나 하는 것을 느끼지 못 했기 때문입니다.
하지만 해밀턴 역학의 의미, 해밀턴 역학의 진수는 정준 변환과 그 이상의 방법을 이해할 때 진정으로 확인할 수 있습니다. 해밀턴 역학의 묘미는 개개의 문제를 푸는데 있는 것이 아니라, 역학 시스템을 이해하는 새로운 시각을 제시하는데 있습니다. 이에 대한 구체적인 예는 "푸앵카레 회귀 정리"에 대해서 다룬 지난 포스팅에서 확인 할 수 있습니다. 뉴턴 역학이나 라그랑주 역학을 통해서는 푸앵카레 회귀 정리와 같은 고전 역학 시스템에 대한 성질을 증명할 수 없었을 것 입니다. 해밀턴 역학에 대한 다음 포스팅 부터 이에 대해서 하나 하나 알아가도록 하겠습니다.
'물리학' 카테고리의 다른 글
| [고전역학-7] 해밀턴 역학 : 해밀턴-야코비 방정식 (1) | 2021.01.22 |
|---|---|
| [고전역학-6] 해밀턴 역학 : 정준 변환의 생성자 (Generator) (0) | 2021.01.19 |
| [고전역학-5] 해밀턴 역학 : 정준 변환 Canonical transformation (3) | 2021.01.17 |
| [고전역학-3]푸앵카레 재귀정리 : 과거와 현재와 미래는 반복 된다! (feat 리우빌 정리) (1) | 2021.01.11 |
| [고전역학-2]사이클로이드가 등시 곡선 임을 증명하는 가장 우아한(?) 방법 (0) | 2021.01.09 |


