미분 방정식을 푸는 방법에 대한 포스팅이랑 수학의 내용을 다루지만, 이 방법을 이용하여 물리 문제를 푸는 것이 포스팅의 목적이기 때문에 이 글의 카테고리를 <물리학>으로 택했습니다.
물리학의 수학적 언어는 미분 방정식이라고 해도 과언이 아닐 정도로 미분 방정식은 물리학의 곳곳에서 나타납니다. 고전 역학을 설명하는 뉴턴의 운동 방정식, 고전 전자기 이론을 설명하는 맥스웰의 방정식, 양자 역학을 설명하는 슈뢰딩거 방정식은 형태는 조금씩 다르지만 모두 시간과 공간에 대한 미분 방정식이라는 것에는 차이가 없습니다. 따라서 개별 현상을 이해하기 위해서는 뉴턴 방정식, 맥스웰 방정식, 슈뢰딩거 방정식에 대한 구체적인 수식을 세우고, 미분 방정식을 풀면 됩니다. 방정식을 푸는 것은 단순한 수학적인 과정이니, 원리적(!)으로 볼 때, 시스템을 기술하는 미분 방정식을 세우면 물리(!) 문제를 모두 이해한 것과 다름 없습니다.
그러나, 개별 자연 현상을 정확하게 이해하기 위해서는 미분 방정식의 해를 직접 구해야 합니다. 원리를 알았다고 해서 현상을 모두 이해한 것은 당연히 아니니까요. 상황에 맞은 미분 방정식을 세웠으면, 실제 실험과 미분 방정식의 해가 일치하는지 혹은 미분 방정식의 해를 통해서 실험이 어떤 방향으로 전개될지에 대한 결과를 얻어야 합니다.
보통 물리 교과서에서는 해석적으로 풀이가 가능한 매우 간단한 형태의 미분 방정식에 대해서 다룹니다. 고전 역학을 예로 든다면 (별다른 언급이 없다면, 모든 예시는 고전 역학 즉 뉴턴의 운동 방정식인 $F = ma$를 푸는것으로 가정하겠습니다), 자유 낙하 운동, 단조화 진동, 케플러 문제($1/r$ 위치 에너지 문제) 는 해석적인 풀이가 가능하고, 이 문제를 집중적으로 풀게 됩니다. 하지만, 실제 자연 현상을 기술하는 미분 방정식은 매우 복잡해서 해석적으로 풀리지 않는 경우가 대부분입니다. 입자와 입자 사이의 힘(혹은 포텐셜)이 매우 복잡한 형태로 주어지거나 혹은 다루어야 하는 입자의 갯수가 많은 경우엔 해석적으로 문제를 푸는것이 매우 어렵습니다. 전자의 예시는 미분 방정식이 비선형 방정식이 되는 경우라 할 수 있고, 후자의 문제는 3체 문제와 같이 해의 형태가 초기 조건에 따라 매우 급격하게 바뀌는 경우라 할 수 있습니다.
따라서, 이런 경우에는 미분 방정식을 컴퓨터를 이용하여 수치적인 방법으로 풀어야 하는데요, 이번 포스팅에서는 수치적인 방법으로 미분 방정식을 푸는 개념을 가장 쉽게 설명할 수 있는 오일러 방법(Euler Method)을 소개하겠습니다. 그리고 이 방법을 이용하여 고전 역학에서 가장 자주 등장하는 문제 중 하나인 조화 진동자 문제를 실제로 풀어 보도록 하겠습니다. 조화 진동자 문제는 해석적인 해를 구할 수 있는 문제이기 때문에, 해석적인 해와 수치해석으로 부터 얻은 해를 비교 할 수 있다는 장점이 있습니다.
1계 상미분 방정식
가장 간단한 형태인 1계 상미분 방정식을 통해 오일러 방법을 소개하도록 하겠습니다. 초기 조건(혹은 일반적으로는 경계 조건)이 부여된 1계 상미분 방정식은 일반적으로
$$\frac{dy}{dt} = f(t, y(t)), y(t_0) = y_0$$
와 같이 쓸 수 있습니다. 여기서 $y$는 $t$에 대한 함수입니다. 우리는 고전 역학 문제를 예시로 들 것이기 때문에 $y$를 입자의 위치, $t$를 시간이라고 생각해도 됩니다. $y(t_0) = y_0$는 초기 조건입니다. 시각 $t_0$에서 입자의 위치가 $y_0$으로 주어진 문제라 할 수 있습니다.
오일러 방법
오일러 방법은 미분의 정의를 이용하여, 직관적으로 미분 방정식을 푸는 방법 입니다. 미분은 다음과 같은 극한으로 정의 되는데,
$$\frac{dy}{dt}(t) = \lim_{h \rightarrow 0}\frac{y(t+h) - y(t)}{h}$$
수치적으로 문제를 풀 때는 $h$를 무한소로보내는 것은 불가능 하기 때문에, 주로 무한소는 아니지만 컴퓨터로 다룰 수 있는 매우 작은 숫자로 근사하여 미분을 계산하기도 합니다. 즉, $h$가 매우 작은 숫자라고 할 때, $t = t$에서
$$y(t+h) \approx y(t) + \frac{dy}{dt} \cdot h = y(t) + f(t, y(t)) \cdot h$$
로 근사가 가능합니다. 이 근사를 $t = t+h$에서 한 번 더 적용하면,
$$y(t+2h) \approx y(t+h) + f(t, y(t+h)) \cdot h$$
가 되고, 이 과정을 계속해서 반복하게 된다면 일반적으로 $t=t_0 + n \cdot h$에서의 함수값은
$$y(t+n \cdot h) \approx y(t+(n-1) \cdot h) + f(t+(n-1) \cdot h, y(t+(n-1) \cdot h)) \cdot h$$
이 됩니다. 이 과정은 시간을 $h$ 간격으로 불연속화 시키고, 불연속화 된 시간에서 함수 $y$의 값을 근사적인 방법으로 구하는 것이라 볼 수 있습니다. 불연속화 한 시간을 초기 값인 $t_0$ 부터 시작하면, $t_0 = t_0, t_1 = t_0 +h, t_2 = t_0 + 2 \cdot h, ..., t_n = t_0 + n \cdot h, ... $와 같이 표현할 수 있고, 이 때의 함수값을 $y_n = y(t_n)$으로 간단히 표시한다면, 바로 위에 쓴 $t = t_n$ 에서의 함수값은
$$y_n \approx y_{n-1} + f(t_{n-1}, y_{n-1}) \cdot h, n = 1, 2, 3, ...$$
이 됩니다. 위 식은 수열 $f_n$의 점화식이고, $y_0$ 값이 주어진다면, 임의의 $n$, 즉 임의의 시간 $t = t_n = t_0 + n \cdot h$ 에서의 함수값을 구할 수 있습니다. 물론 이 값은 정확한 값이 아니라 근사값 입니다.
오일러 방법을 이용한 1계 상미분 방정식 풀이의 예시 : 속도에 비례하는 저항을 받은 낙하 운동
중력장에 의해 자유 낙하 하는 물제의 미분 방정식을 생각하겠습니다. 단순히 중력만 작용한다면 문제가 너무 간단해지기 때문에, 속도에 비례하는 저항력을 추가하겠습니다. 이 경우 속도에 대한 미분 방정식은
$$F = mg - kv = \frac{dv}{dt}, v(t=0) = 0$$
가 됩니다. 여기서 $m$은 질량, $g$는 중력 가속도, $k$는 공기 저항 상수 입니다. 문제를 간단하게 하기 위해서 $m = g = k = 1$와 같이 모든 상수를 그냥 1로 두겠습니다. 이렇게 간단히 한다면 우리가 풀어야 하는 문제는
$$\frac{dv}{dt}(t) = 1 - v(t), v(t=0) = 0$$
가 됩니다. 이 문제를 오일러 방법으로 풀면 되는데요, $t \in [t_0, t_1] = [0, 5]$ 구간에서 해를 구하도록 하겠습니다. 오일러 방법에서는 시간 $t$의 단위 $h$를 정해야 하는데, $h = 0.1$로 정의하겠습니다. 이 경우 $t_1 = 5 = t_{50}$이 됩니다. 오일어 방법의 수열의 점화식, $v_n \approx v_{n-1} + f(t_{n-1}, v_{n-1}) \cdot h$ 에 $f(t, v) = 1 - v$를 대입하여 수열의 점화식을 최종적으로 쓰면,
$$v_n = v_{n-1} + (1-v_{n-1}) \cdot h, v_0 = 0$$
가 됩니다. $v_0, v_1, v_2, ..., v_{50}$까지 구해주면 되는데 사람이 손으로 하면 매우 귀찮고 시간이 오래 걸리는 일이니 컴퓨터 프로그래밍을 통해 구해야 하는데요, 파이썬을 이용하여 코드를 작성하면 다음과 같이 할 수 있습니다. 파이썬 프로그래밍을 할 수 있다면, 아래 코드를 복-붙하고 실행하면 됩니다.
import numpy as np
from matplotlib import pyplot as plt
def gravity():
t0, t1 = 0, 5
N = 50
h = (t1-t0)/N
v0 = 0
vs = [v0]
for i in range(1, N):
v1 = v0 + (1-v0)*h
vs.append(v1)
v0 = v1
ts = np.linspace(t0, t1, N)
va = 1 - np.exp(-ts)
plt.scatter(ts, vs, color = 'blue', label = "Euler")
plt.plot(ts, va, color = 'red', lw = 2, label = "Analytic")
plt.legend(ncol=3, fontsize='small', loc="upper left")
plt.xlabel("Time")
plt.ylabel("y")
plt.grid()
plt.show()
if __name__ == '__main__':
gravity()
결과는 위 그래프와 같습니다. 푸른색 점으로 표시한 것이 오일러 방법을 통해서 $t = t_n$에서 구한 $v_n = v(t_n)$의 값이고, 붉은색 선으로 그린 것이 이 미분 방정식의 해석적인 해인 $v(t) = 1-e^{-t}$입니다. (이 미분 방정식은 간단한 선형 방정식이기 때문에, 해석적인 방법으로 해를 구할 수 있습니다)

수치적으로 미분 방정식을 푸는 것은 어쩔 수 없이 해를 근사적으로 구하는 것 이기 때문에, 해석적인 해와 비교하면 에러가 발생할 수 밖에 없는데, $t=1$ 근방에서 에러가 가장 큰데, 약 $0.012$ 정도가 됩니다. 에라가 조금 있긴 하지만, 전체적으로 봤을 때, 해석적인 해와 수치적인 해가 매우 일치함을 확인할 수 있습니다. (해석적인 해를 쉽게 구할 수 있는 경우라서 유용성이 없어 보일 수 도 있지만) 수치적인 방법은 임의의 복잡한 방정식에 대해서 프로그래밍을 통해서 해를 구할 수 있다는 큰 장점이 있습니다.
오일러 방법은 시간을 불연속화 하는 크기 $h$에 따라서 에러가 정해지는데, 당연하게도 $h$가 작으면 작을 수록 에러가 작아 집니다. 위 예시에서는 $h=0.1$을 통해서 계산하였는데, 만일 $h = 0.01, 0.001$로 줄여서 계산한다면, 이 계산의 오차는 아래 그래프와 같게 됩니다.

$h=0.1$의 최대 오차는 약 $0.012$, $h=0.01$의 최대 오차는 약 $0.0012$, $h=0.001$의 최대 오차는 약 $0.00012$로 $h$가 $1/10$씩 줄어들 때 마다, 오차 역시 $1/10$씩 줄어들게 됩니다.
일반적으로 오일러 방법에서는 미분을 $h$의 1차식까지 정확히 구하고 $h^2$ 이상의 항은 무시합니다. 따라서 각 시간 간격 $t_{n}$과 $t_{n+1}$에서 $h^2$에 비례하는 에러가 생기게 됩니다. 그리고 시간의 불연속 값을 $h$라고 둔다면, 전체 시간 구간은 $\frac{1}{n}$에 비례하는 갯수로 구분 됩니다. 따라서, 전체적으로 보면 에러의 크기는 $h^2 \cdot \frac{1}{h} = h$에 비례하게 됩니다.
2계 상미분 방정식
2계 상미분 방정식은 일반적으로
$$y''(t) = f(t, y, y'), y(t_0) = y_0, y'(t_0) = y'_{0}$$
와 같이 쓸 수 있습니다. 편의상 미분을 $'$ 표시로 하겠습니다.
2계 상미분 방정식은 2개의 연립 1계 상미분 방정식으로 풀 수 있습니다. 즉, $z = y', z(t=0)= y'_0$와 같이 $z(t)$를 정의하면, 위 $y$에 대한 2계 미분 방정식은
$$z'(t) = f(t, y, z)$$
$$y'(t) = z(t), y(0) = y_0, z(0) = y'_0$$
와 같이 2개의 미분 방정식으로 표현할 수 있습니다. 풀어야 하는 미분 방정식이 2개로 늘어났지만, 이 과정을 거치고나면 $y$에 대한 2계 미분 방정식은 $y, z$에 대한 1계 미분 방정식으로 변했다는 장점이 있습니다. 1계 미분 방정식의 풀이법은 위에서 설명했으니, 그 방법을 통해서 $y_{n-1}, z_{n-1}$을 이용하여 $y_n, z_n$에 대한 식을 세우면 됩니다. 어렵지 않게,
$$y_{n+1} = y_{n} + z_n \cdot h$$
$$z_{n+1} = z_n + f(t_n, y_n, z_n) \cdot h$$
을 얻을 수 있습니다. $(y_0, z_0) = (y_0, y'_0)$을 시작으로 $n=1, 2, 3, 4, ...$ 을 계속 반복해 주기만 하면 됩니다.
위 식에서 $y'$을 $z$라고 하였는데, $y$가 입자의 위치라고 한다면 $z$는 입자의 속도가 됩니다. 즉, 가속도를 위치에 대해서 표현하면 위치의 2계 미분이 되지만, 속도로 표현하면 1계 미분이 되는 것과 같은 방식으로 2계 미분 방정식을 1계 미분 방정식으로 쓸 수 있는 것 입니다. 이 경우에 해는 $(y, v)(t)$ 와 같이 위치와 속도로 이루어진 2차원 좌표상의 점으로 표시할 수 있는데, 위치와 속도(좀 더 정확히는 운동량)으로 이루어진 공간을 위상 공간(phase space)이라고 합니다. 위상 공간에 대해서는 고전역학에 대한 포스팅을 많이 해 두었으니, 그 포스팅들을 통해 위상 공간의 물리적인 의미를 알 수 있습니다. 운동 방정식의 해를 단순히 $y(t)$로만 표현하는 것이 아니라 위상 공간에서의 궤적으로 표현하면 더 흥미롭게 문제를 풀 수 있는데, 이는 이번 포스팅의 직접적인 주제는 아니기 때문에 이에 대한 설명은 생략 하도록 하겠습니다.
오일러 방법을 이용한 2계 상미분 방정식 풀이의 예시 : 단조화 진동자
역학에서 나오는, 아니 모든 물리학을 통틀어서, 가장 중요한 2계 상미분 방정식은 단조화 진동자의 운동 방정식 입니다. 단조화 진동자의 운동 방정식은 (자유도를 $y$로 쓸 때),
$$y''(t) = -y(t), y(0) = y_0, y'(0) = y'_0, t \in [t_0, t_1]= [0, 3 \cdot 2 \pi]$$
로 주어집니다. 위에서와 같이 편의상 모든 물리 상수는 $1$로 간단히 하였고, 초기 조건은 초기 위치와 초기 속도가 주어지는 경우로 가정하였습니다. 시간의 영역은 진동 주기 $2 \pi$의 $3$배로 하였습니다. 이제 이 문제를 위 $y_n, z_n$을 구하는 점화식을 통해서 구하면 됩니다. 앞의 문제의 코드에서 변수 하나를 더 추가 하면 되는데, 쉽게 할 수 있는 코드는 아래와 같습니다.
import numpy as np
from matplotlib import pyplot as plt
def harmonic():
t0, t1 = 0, 3*(2*np.pi)
N = 3000
h = (t1-t0)/N
y0, z0 = 1, 0
ys = [y0]
for i in range(1, N):
y1 = y0 + z0 * h
z1 = z0 - y0 * h
ys.append(y1)
y0 = y1
z0 = z1
ts = np.linspace(t0, t1, N)
ya = np.cos(ts)
plt.plot(ts, ys, lw = 2, label = "Euler", color = "blue")
plt.plot(ts, ya, lw = 2, label = "Analytic", color = "red")
plt.legend(ncol=3, fontsize='small', loc="upper left")
plt.xlabel("Time")
plt.ylabel("y")
plt.grid()
plt.show()
if __name__ == '__main__':
harmonic()
결과는 위 그래프와 같습니다. 푸른색 선은 오일러 방법으로 구한 해, 붉은색 선은 해석적인 방법으로 구한 해 $y(t) = \cos t$입니다. 시간의 구간 $t \in [0, 3 \cdot 2 \pi]$ 를 $3000$개의 구간으로 나누어 계산하였습니다. 즉, $h = \frac{3 \cdot 2 \pi}{3000} = \frac{2 \pi}{1000} \approx = 0.00628$ 입니다. 전체적으로 두 그래프의 개형이 일치합니다. 구간에서 총 3번 주기 운동을 하며 진폭은 대략 $1$입니다. 하지만, 시간 $t$가 커질 수록 해석적인 해와 수치적인 해의 차이가 보이는데, 특히 $y = \pm 1$ 부근에서 차이가 두드러집니다. 해석적인 해는 항상 $-1, 1$ 값을 갖지만, 수치적인 해는 $-1$ 보다 더 작거나 $1$ 보다 더 큰 값을 갖게 됩니다. 수치적인 해법으로 근사적인 해를 구했기 때문에 생기는 피할 수 없는 에러 입니다.
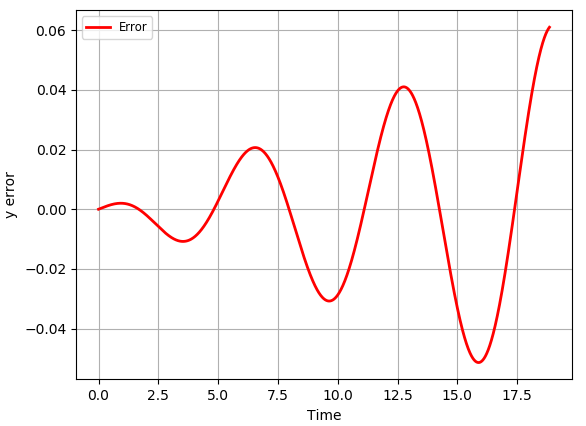
시간에 따른 에러의 크기를 그리면 위와 같습니다. 에러의 크기가 시간에 따라서 계속 증가한다는 것은 볼 수 있습니다. 시간을 불연속적으로 만들어 주는 크기 $h$을 줄이면 줄일수록 에러의 크기가 줄어든다는 것을 앞의 예시를 통해서 확인했는데, 따라서 $h$를 더 작은 숫자로 줄이면 에러를 줄일 수 있기는 하지만, 에러가 시간에 커짐에 따라서 저렇게 증가한다면 $h$을 아무리 작게 잡는다 하더라도 에러는 자꾸 커지게 되어 종국에는 우리가 원하는 정확도 보다 에러가 더 커질 수 있습니다.
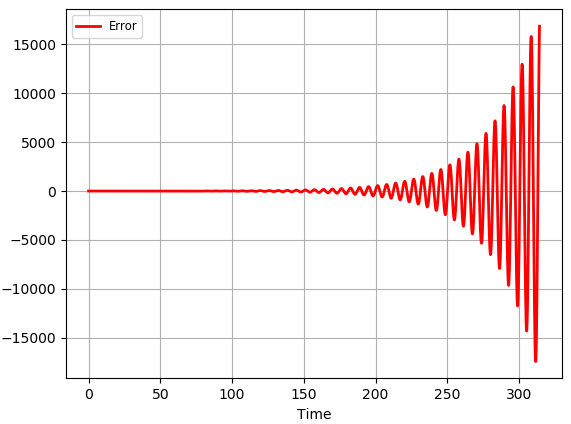
시간의 범위를 $t = 50 \cdot 2 \pi$까지 구해하고, 해석적인 해와의 차이를 그렸습니다. $h = \frac{50 \cdot 2 \pi}{5000}$ 로, 전체 시간 구간은 $5000$개의 조각으로 나눈 것 입니다. 바로 앞 문단에서 언급한 것과 같이 시간이 커짐에 따라서 에러의 크기도 같이 커지는 것은 확인할 수 있는데, 에러가 증가하는 경향은 거의 지수적으로 증가합니다.
실제로 에러의 크기의 상한을 구할 수 있는데, 그 크기는
$$\frac{hM}{2L} \Big( e^{L(t-t_0)}-1\Big)$$
입니다. 여기서 $M$는 시간 $t$의 정의역에서 $|y''|$의 최대값이며, $L$은 $y$에 따라 정해지는 상수(정확히는 리프쉬츠 상수) 입니다. 결국 에러의 (최대값의) 크기는 $h$에 비례하고, 시간 간격의 크기 $t-t_0$에 지수적으로 크게 증가하게 됩니다. 위 예시에서 실제로 얻은 에러의 변화량 역시 이 식과 일치합니다.
오일러 방법의 한계
오일러 방법은 매우 직관적이라는 장점과, 매우 쉽게 프로그래밍을 할 수 있다는 장점이 있습니다. 실제 위 프로그램 코드의 예시와 같이 10줄 이내로 코드를 작성할 수 있습니다. (위 전체 코드는 10줄이 넘는데, 그래프를 그리기 위한 부분을 제외하고 순수하게 오일러 방법으로 $y_n$을 구하는 것만 고려한다면 10줄 이내 입니다)
하지만, 매우 거친 근사를 하는 탓에, 해석적으로 정확한 해와 수치적으로 얻은 해 사이에 에러가 매우 커짐을 확인할 수 있었습니다. 시간의 불연속 값 $h$를 줄이게 되면 에러가 $h$에 비례해서 줄어들게 되지만, 이렇게 되면 정해진 시간 구간에서 반복 계산 해야하는 값이 $\frac{1}{h}$에 비례해서 증가하기 때문에 계산 시간이 늘어난다는 단점이 있습니다. $h$를 매우 줄인다고 하더라도, 계산하는 시간 간격 $t - t_0$에 대해서 에러는 지수적으로 증가하기 때문에, 에러가 자꾸자꾸 커지는 것을 피할 수 없게 됩니다.
따라서, 오일러 방법의 단점을 극복하는 방법이 매우 많이 고안되었는데, 그 중에서 대표적인 방법은 룽게-쿠타 방법(Runge-Kutta method)입니다. 이 방법에 대해서는 다음 포스팅에서 알아 보도록 하겠습니다.
'물리학' 카테고리의 다른 글
| 룽게-쿠타 방법(Runge-Kutta method) 을 활용하여 보다 빠르고 정확하게 미분 방정식 문제를 수치 해법으로 풀기 + 파이썬 코드 (0) | 2021.10.15 |
|---|---|
| 수치 미분 방정식 풀이법을 이용하여 최종값 조건이 주어진 문제 풀기 : 슈팅 방법 (0) | 2021.10.15 |
| 대칭성을 이용한 2차원 단조화 진동자 문제 풀이 (0) | 2021.09.13 |
| 슈뢰딩거 방정식 유도 : 슈뢰딩거의 1926년 논문의 유도 과정을 이해하자 (4) | 2021.09.07 |
| [고전역학-10] 해밀턴 역학 : 시간에 무관한 해밀턴-야코비 방정식, 기하학적인 의미, 입자의 운동을 파동 처럼 생각하기 (1) | 2021.09.05 |


