지난 포스팅 https://studyingrabbit.tistory.com/53
수치 미분 방정식 풀이법과 이를 이용한 고전 역학 문제 해결 : 오일러 방법(Euler method)을 이용하
미분 방정식을 푸는 방법에 대한 포스팅이랑 수학의 내용을 다루지만, 이 방법을 이용하여 물리 문제를 푸는 것이 포스팅의 목적이기 때문에 이 글의 카테고리를 <물리학>으로 택했습니다. 물리
studyingrabbit.tistory.com
에서 미분 방정식을 수치 해법으로 풀 수 있는 가장 간단한 방법인 오일러 방법에 대해서 알아 봤습니다. 간단히 복습을 하면 오일러 방법은
(1) 시간을 기본 단위 $h$를 이용하여 불연속적인 값으로 바꾸고, 각 시각을 $t_n$으로 표현
(2) 미분값을 근사적으로 계산 $f(t + h) \approx f(t) + h \cdot f'(t)$ 하여 $f(t_{n+1})$ 값을 $f(t_n), f'(t_n), ...$으로 표현
(3) 위 $f(t_n) = f_n$에 대한 점화식을 컴퓨터를 이용하여 원하는 $n$까지 계산
와 같은 방법으로 미분 방정식을 풀게 됩니다. 개념적으로나, 컴퓨터 프로그래밍적으로나 매우 간단한 방법입니다. 하지만, $t_n$값이 커질 수록 해석적인 해와 수치 해법으로 구한 해의 차이(에러)가 지수적으로 증가하게 된다는 단점이 있다는 것도 확인하였습니다. 따라서 매우 정교한 계산을 하기 위해서는 오일러 방법을 채택하는 것은 결코 좋지 못 합니다. 물론 $h$값을 무한히 작게 하면 에러의 크기가 크지 않을 테지만, 이 경우에는 원하는 시간 간격 $t_1 - t_0$에서 계산해야하는 횟수가 $\frac{t_1 - t_0}{h}$와 같이 엄청 커지기 때문에 계산 시간이 매우 오래 걸리게 됩니다.
따라서, 실제 응용을 위해서는 오일러 방법보다 효율적인 방법을 이용해야 합니다. 즉, 계산 시간(량)은 오일러 방법과 유사하면서 계산의 정확도는 훨씬 높은 방법을 이용해야 합니다. 이러 방법 중 대표적인 방법이 바로 이번 포스팅에서 알아볼 룽게-쿠타 방법 (Runge-Kutta method) 입니다.
초기값이 주어진 미분 방정식
$$y'(t) = f(t, y), y(t_0)= y_0, t \in [t_0, t_f]$$
를 룽게-쿠타 방법으로 풀어 보도록 하겠습니다. 우선, 구간 $[t_0, t_f]$의 시간을 $N$조각 하여 시간의 불연속 간격을 $h = \frac{t_f - t_0}{N}$으로 잡겠습니다. 이때, 임의의 시간 $t_n = t_0 + n \cdot h$와 같이 나타앨 수 있습니다. 각 $t_n$에서 함수값 $y(t_n)$을 편의상 $y_n$으로 쓴다면, 룽게-쿠타 방법에 의해 $t_{n+1}$에서의 함수값 $y_{n+1}$의 점화식은 다음과 같이 주어집니다.
$$y_{n+1} = y_n + \frac{1}{6} h \Big(k_1 + 2k_2 + 2k_3 + k_4 \Big)$$
$$k_1 = f(t_n, y_n)$$
$$k_2 = f\Big(t_n + \frac{h}{2}, y_n + h \frac{k_1}{2} \Big)$$
$$k_3 = f\Big(t_n + \frac{h}{2}, y_n + h \frac{k_2}{2} \Big)$$
$$k_4 = f(t_n+h, y_n+hk_3)$$
오일러 방법에서는 $y$의 증분 $y_{n+1} - y_n$은 $h \cdot f(t_n, y_n)$와 같이 $(t_n, y_n)$에서의 함수값 $f(t_n, y_n)$을 사용하였는데, 룽게-쿠타 방법에서는 $f(t_n, y_n)$ 대신 $f(t_n, y_n), f\Big(t_n + \frac{h}{2}, y_n + h \frac{k_1}{2} \Big), f\Big(t_n + \frac{h}{2}, y_n + h \frac{k_2}{2} \Big), f(t_n+h, y_n+hk_3)$를 $1:2:2:1$로 가중 평균을 취한 값을 사용한다는 것이 큰 특징입니다.
$f(t, y)$에서 $t$ 항만 고려한다면, $k_1$에서는 구간의 초기 값인 $t_n$을, $k_2, k_3$에서는 $t_n$과 $t_{n+1}$의 중간값(평균값)인 $t_n + \frac{h}{2}$를, $k_4$에서는 구간의 마지막 값인 $t_{n+1}$를 사용합니다. $y$항도 초기 값, $y_n$, 근사된 중간 값과 근사된 마지막 값을 사용합니다. 오일러 방법이 구간 $[t_n, t_{n+1}]$에서 초기값만 이용한다면, 룽게-쿠타 방법에서는 $[t_n, t_{n+1}]$의 여러 점에서의 값을 이용한다는 차이가 있습니다. 여러점의 정보를 이용하는 만큼, 룽게-쿠타 방법은 오일러 방법에 비해 더 정확한 결과를 줍니다.
룽게-쿠타 방법 역시 당연히 근사적인 방법이기 때문에 해석적인 방법과 비교하여 에러가 존재하는데, 한 시간 단위 $h$에서 생기는 에러는 $h^5$에 비례하게 됩니다. $h^2$에 비례하여 에러가 생기는 오일러 방법 보다 훨씬 더 에러의 수준이 작습니다. $h$값을 초기 시간과 마지막 시간을 $N$개로 나눈 구간의 크기 $h = \frac{t_f - t_0}{N}$로 정의했기 때문에, 구간의 크기 $N$은 $\frac{1}{h}$에 비례하게 되고, 따라서 누적 에러의 크기는 $h^4$에 비례하게 됩니다. 여기서 누적 에러란 시간의 마지막 값인 $t_f$에서 생길 수 있는 에러를 뜻 합니다.
에러의 크기를 $h$로 표현했는데, 이를 $N$으로 표현하면, 최종 에러는 룽게-쿠타 방법에서는 $\frac{1}{N^4}$에 비례하게 되고, 오일러 방법에서는 $\frac{1}{N^1}$에 비례하게 됩니다. 예를들어, 에러의 크기를 $0.0001$ 보다 줄이고 싶다면, 오일러 방법에서는 $N = 10,000$ 정도로 잡고 계산을 해야하지만, 룽게-쿠타 방법에서는 $N=10$정도로 잡고 계산하면 됩니다. 즉, 룽게-쿠타 방법을 이용한다면 계산을 훨씬 줄이고도 오일러 방법과 동일한 수준의 에러를 갖게 됩니다. 룽게-쿠타 방법을 오일러 방법에 비해 매우 매우 효율적인 방법입니다.
실제 문제를 룽게-쿠타 방법으로 풀어 보자.
실제 문제를 오일러 방법과 룽게-쿠타 방법으로 구하고 두 결과의 차이를 비교해 보도록 하겠습니다. 역시 가장 간단한 문제는 고전 역학의 단조화 진동자 문제 입니다. 모든 물리 상수를 $1$로 두고, 1차원 상의 자유도를 $y(t)$를 이용하여 표현하면, 우리가 풀어야 하는 초기 조건이 주어진 미분 방정식은
$$y''(t) = -y(t), y(t_0)= 0, y'(t_0) = 1, t \in [t_0 = 0, t_f = 5 \cdot 2 \pi]$$
이 됩니다. 초기 위치는 $0$, 초기 속도는 $1$로 편의상 가정 하였고, $5$번 주기 운동을 하는 시간 동안 $y(t)$를 계산해 보도록 하겠습니다.
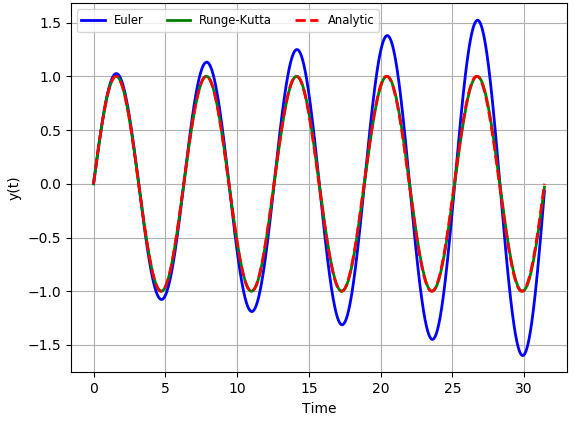
결과는 위 그래프와 같습니다. 시간 구간 $[0, 5 \cdot 2 \pi]를 $N = 1000$ 조각으로 나누어 계산하였습니다.
붉은색으로 표시한 그래프가 해석적인 해 $y(t) = \sin t$, 녹색으로 표시한 그래프가 룽게-쿠타 방법으로 구한 해, 파란색으로 표시한 그래프가 오일러 방법으로 구한 해 입니다. 바로 볼 수 있는 것과 같이, 해석적인 해와 룽게-쿠타 방법으로 구한 해의 차이는 거이 없습니다. 녹색 그래프와 붉은색 그래프가 거의 완전히 겹쳐져서 보입니다. 그에 반에, 시간이 커질 수록 파란색 그래프는 붉은색 그래프의 차이는 점점 커지게 됩니다. 한 주기 동안의 해는 크게 차이가 없지만, 마지막 다섯 번째 주기 운동에서의 차이는 눈에 띄게 커집니다.

해석적인 해와의 차이를 그리면 위 그래프와 같습니다. 룽게-쿠타 방법으로 푼 경우, 위 구간에서 에러의 최대값은 $0.025$ 수준이지만, 오일러 방법으로 푼 경우에는 $0.45$ 정도로 매우 큽니다. 이 정도라면 오일러 방법을 이용한다면 완전히 잘못된 결과를 얻게 된다고 볼 수 있습니다.

위 그래프는 오일러 방법에 사용한 $N$과 룽게-쿠타 방법에서 사용한 $N$를 서도 다르게 두고 계산한 결과 입니다. 오일러 방법에서는 $N = 10^5$을, 룽게-쿠타 방법에서는 $N = 10^2$를 사용하였습니다. 약간의 차이가 있긴 하지만, 두 경우 모두 해석적인 해와 거의 유사합니다. 즉, 오일러 방법을 사용할 때 보다, 룽게-쿠타 방법을 이용한다면 계산량을 $10^5$에서 $10^2$으로 $\frac{1}{1000}$만큼 줄일 수 있습니다.
위 계산을 하기 위해 생성한 파이썬 코드 입니다. 파이썬 프로그래밍을 할 수 있다면, 다양한 형태의 힘에 대해서 시뮬레이션을 해 볼 수 있습니다.
import numpy as np
from matplotlib import pyplot as plt
def force(t, x, v):
"""
가속도 정의. 모듈의 이름은 force이지만, 사실은 가속도
"""
return -x
def velocity(t, x, v):
"""
속도는 단순한 속도
"""
return v
def rungekutta_method(x0, v0, t0, t1, N):
"""
x0 : 초기 위치
v0 : 초기 속도
t0 : 초기 시각
t1 : 최종 시각
N : t0-t1 구간을 N 조각으로 불연속화
"""
xs, vs, ts= [x0], [v0], np.linspace(t0, t1, N)
h = (t1 - t0) / N
for i in range(1, N):
t = t0 + h*(i-1)
"""
룽게-쿠타 법칙에 따라서 k1, k2, k3, k4를 x, v에 대해서 계산
위치(x)와 속도(v)를 동시에 계산
"""
k1x = velocity(t, x0, v0)
k1v = force(t, x0, v0)
k2x = velocity(t+h/2, x0+h*k1x/2, v0+h*k1v/2)
k2v = force(t+h/2, x0+h*k1x/2, v0+h*k1v/2)
k3x = velocity(t+h/2, x0+h*k2x/2, v0+h*k2v/2)
k3v = force(t+h/2, x0+h*k2x/2, v0+h*k2v/2)
k4x = velocity(t+h, x0+h*k3x, v0+h*k3v)
k4v = force(t+h, x0+h*k3x, v0+h*k3v)
"""
룽게-쿠타 법칙에 따라서 x, v 를 업데이트
"""
x1 = x0 + h*(k1x + 2*k2x + 2*k3x + k4x)/6
v1 = v0 + h*(k1v + 2*k2v + 2*k3v + k4v)/6
xs.append(x1)
vs.append(v1)
x0 = x1
v0 = v1
return ts, xs, vs
def harmonic_oscillator():
"""
계산할 조건 입력
"""
t0, t1 = 0, 5*(2*np.pi)
x0, v0 = 0, 1
N = 1000
"""
룽게-쿠타 방법을 이용하여 미분 방정식 계산
"""
T, X, V = rungekutta_method(x0, v0, t0, t1, N)
"""
matplotlib 라이브러리를 이용하여 (t, x) 그래프를 생성
"""
plt.plot(T, X, lw = 2, color = "green", label = "Runge-Kutta")
plt.xlabel("Time")
plt.ylabel("y(t)")
plt.grid()
plt.show()
plt.close('all')
if __name__ == '__main__':
harmonic_oscillator()
'물리학' 카테고리의 다른 글
| 슈뢰딩거 방정식을 수치 해법으로 풀기 (2): 단조화 진동자 문제 풀기, 고유값이 아닌 에너지 값에 대응되는 파동 함수의 개형은? (0) | 2021.10.17 |
|---|---|
| 슈뢰딩거 방정식을 수치 해법으로 풀기 (1): 슈팅 방법으로 알아보는 고유값 문제, 무한 포텐셜 우물 문제 풀기 (0) | 2021.10.16 |
| 수치 미분 방정식 풀이법을 이용하여 최종값 조건이 주어진 문제 풀기 : 슈팅 방법 (0) | 2021.10.15 |
| 수치 미분 방정식 풀이법과 이를 이용한 고전 역학 문제 해결 : 오일러 방법(Euler method)을 이용하여 조화 진동자 문제 풀기 (1) | 2021.10.12 |
| 대칭성을 이용한 2차원 단조화 진동자 문제 풀이 (0) | 2021.09.13 |



