동역학계dynamical system
동혁학계이란 시간에 따라 변화하는 상태를 기술하는 수학 혹은 물리학의 분야 입니다. 뉴턴의 운동 방정식에 따라서 입자가 공간상에서 움직이는 것(위치가 변화하는 것)은 동역학계의 가장 대표적이면서 가장 오래된 연구 주제 중 하나 입니다. 사실, 수학의 분야로의 동역학계는 물리학의 뉴턴의 방정식을 보다 추상적이고 체계적으로 공부하기 위해 탄생한 분야입니다. 좀 더 수학적으로 엄밀하게 정의하면(그러나 수학자들이 보기에는 엉성한), 동역학계는 (시간, 상태, 함수) 이 세 요소로 구성이 되는데, 시간은 말 그대로 시간이라 볼 수 있고, 상태는 시간에 따라 변화를 하는 대상이 입니다. 함수는 시간에 따라 상태가 어떻게 변화하는지를 결정합니다. 앞에서 예시로 들었던 운동 방정식에서는 시간은 실제로 물리적인 시간이며, 상태는 입자의 (위치, 운동량)이며, 함수는 뉴턴의 운동 방정식이 됩니다.
미분방정식에 의해 기술되는 동역학계
다양한 형태의 동역학계 중에서 가장 기본적인 동역학계는 시간에 따른 상태의 변화가 미분방정식에 의해 기술되는 시스템 입니다. 뉴턴의 운동 방정식에 의해 입자의 위치가 기술되는 것은 이에 좋은 예시 입니다. 뉴턴 역학에서 입자의 상태는 위상 공간phase space에서의 한 점으로 주어지는데, 이 점은 (위치, 속도)의 값을 갖습니다 (정확히는 속도가 아니라 운동량이지만, 편의상 속도라고 하도록 하겠습니다). 시간에 따른 (위치, 속도)을 $(x(t), v(t))$라고 한다면, $(x(t), v(t))$의 시간에 따른 변화는 미분 방정식
$$\dot{x}(t) = v(t)$$
$$\dot{v}(t) = f(t, x, v)$$
에 의해 기술됩니다. $\dot{O}$ 표시는 $O(t)$의 시간에 대한 미분을 의미 합니다. 물론 초기 위치와 초기 속도 $(x_0, v_0)$가 주어져야 합니다. 위 식에서 $f(t, x, v)$ 는 뉴턴 역학에서는 힘에 해당하는 함수로, 수학적으로 동력학계를 생각할 때는 힘이 아닌 함수로 추상화 할 수 있습니다. 속도의 변화를 기술하는 함수 $f$는 일반적으로 시간 뿐 아니라, 위치와 속도의 함수 일 수 있습니다.
위 식은 연립 미분방정식으로 일반적인 형태의 $f$에 대해서는 해석적인 해를 찾는 것이 불가능 합니다. 그러나 특수한 형태의 $f$에 대해서는 해석적인 해를 구할 수 있거나 해석적인 해 그 자체는 구할 수 없다고 하더라도 해가 만족해야 하는 성질을 해석적인 방식으로 유도할 수 있습니다. 대표적인 예로, $f(t, x, v) = -x$ 로 주어졌다면, 이 동역학계는 물리학에서의 단조화 진동자를 기술하게 됩니다. 이 포스팅을 읽는 분이시라면 단조화 진동자의 해 정도는 쉽게 구할 수 있을 것 입니다.
더핑 방정식Duffing equation
$f(t, x, v) = -\alpha x -\beta x^3 - \delta v$로 주어지는 동역학계를 생각해 보겠습니다. 이 시스템은 더핑 방정식Duffing equation이라고 합니다. 실제로는 우변에 $\gamma \cos (\omega t)$와 같이 물리적으로 본다면 주기적인 외력 항을 포함한 방정식을 의미하지만, 이번 포스팅에서는 편의상 이 항은 생략 하도록 하겠습니다. 혹은 $\gamma = 0$ 인 특수한 문제를 푼다고 생각해도 됩니다. $f$는 $(x, v)$에 대해서 비선형항을 포함하고 있기 때문에, 일반적으로 해석적으로 푸는 것이 불가능하고, 컴퓨터를 이용한 수치적 해법을 통해 연구를 합니다. 블로그에서 수치적인 방법으로 미분 방정식을 푸는 것은 매우 많이 했기 때문에, 이에 대한 설명은 생략하도록 하겠습니다.
더핑 방정식을 단순히 수학적인 미분 방정식으로 이해할 수 도 있지만, 물리적인 시스템을 기술하는 것에 근원을 두고 있는 방정식인지라 물리적인 방식으로 이해를 한다면, 수학 문제를 푸는데 큰 도움이 될 수 있습니다. $f$는 힘으로 해석할 수 있기 때문에, $-\delta v$는 속도에 비례하는 저항력으로 생각할 수 있습니다. 또한, $-\alpha x - \beta x^3$ 항은 $V(x) = \frac{1}{2}\alpha x^2 + \frac{1}{4} \beta x^4$ 로 주어지는 위치 에너지에 의한 힘으로 생각할 수 있습니다. $\alpha = -1, \beta = 1$ 이라고 한다면, $V(x)$의 개형은 아래와 같습니다.
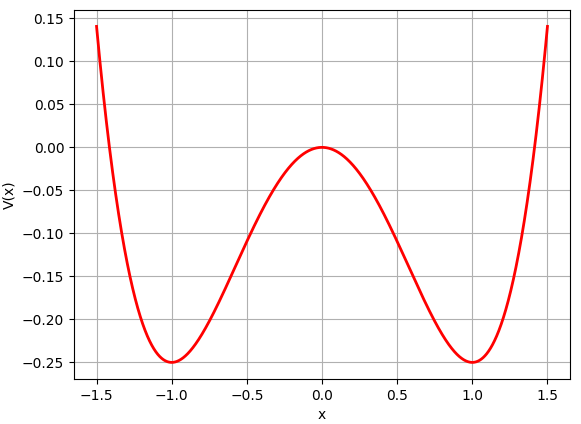
이와 같은 형태의 위치 에너지를 물리학에서는 주로 double well potential 이라고 하는데, 말 그대로 왼쪽(음수 쪽)에 $x = -1$을 중심으로 하는 하나의 깊은 우물이 있고, 오른쪽(양수 쪽)에 $x = 1$을 중심으로 하는 또 하나의 깊은 우물이 있기 때문에 붙여진 이름 입니다. 일반적으로 $\alpha \lt 0, \beta \gt 0$인 경우 $V(x)$의 개형은 위와 같습니다.
수치적인 해법을 이용해서 문제를 풀기 전에 위 $V(x)$의 형태를 통해서 정성적인 방법으로 해의 형태를 예상할 수 있습니다. 우선, $\delta = 0$인 경우를 가정하겠습니다. 앞서 언급한 대로 $-\delta v$항은 속도에 비례하는 저항력으로 생각할 수 있는데, $\delta = 0$이기 때문에, 이 시스템의 입자의 운동은 저항이 없이 위치 에너지 $V(x)$에 의해 결정됩니다. 다양한 초기 상태에 따라서 $x(t), v(t)$가 어떠한 형태를 가질지 물리적인 직관을 통해서 예측해 보겠습니다.
만일 초기 속도$v_0$가 0이고, $0 \lt x_0 \lt \sqrt{2}$ 인 경우, 입자의 위치 에너지는 음수가 되고, 따라서 $(x_1, x_2)$ 사이를 진동하게 됩니다. 여기서 $(x_1, x_2)$는 $x_0$에 대해서
$$V(x_0) = V(x_1) = V(x_2)$$
를 만족하는 $x_1, x_2(\ge x_1)$를 의미 합니다. 당연히 물리적인 직관에 따라서, $x_0 = x_1$이거나, $x_0 = x_2$가 되고, $x_0, x_1, x_2$는 모두 같은 부호를 갖게 됩니다. $-\sqrt{2} \lt x_0 \lt 0$ 인 경우는 앞에서 설명한 것과 $x = 0$에 대해서 대칭인 경우 입니다.
$|x_0| \gt 2$인 경우, 입자의 위치 에너지는 양수가 되고, 입자는 한 쪽 우물에 갖혀 있는 것이 아니라 양쪽 우물을 오가는 운동을 하게 됩니다. 물론 우물의 높이는 무한하기 때문에, 우물 밖을 벗어날 수는 없고,
$$V(x_0) = V(x_1) = V(x_2)$$
를 만족하는 $x_1, x_2(\ge x_1)$에 대해서 $(x_1, x_2)$사이를 오가는 진동 운동을 하게 됩니다.
$v_0 \ne 0$ 인 경우에는 역학적 에너지 보존 $\frac{1}{2}v^2 + V(x) = \frac{1}{2}v_0^2 + V(x_0)$에 의해서 $(x, v)$가 정해집니다. 따라서, $x_0 \in (0, \sqrt{2})$로 초기 위치가 오른쪽 우물안으로 주어졌다고 하더라도 $v_0$가 충분히 크다면, 오른쪽 우물에 갖혀 있지 않고, 양쪽 우물을 번갈아 가며 움직일 수 있습니다.
정리하면, $\delta = 0$ 인 경우에는 $x_0$의 값에 따라 $x(t)$가 진동할 수 있는 범위가 달라지긴 하지만, 어쨌든 $x(t)$는 특정한 구간을 지속적으로 진동하는 형태를 갖게 됩니다.
$\delta \gt 0$ 인 경우
$\delta \gt 0$인 경우, 즉 물리적으로 생각하면 저항이 있는 경우에는 운동의 양상이 완전히 달라집니다. 단조화 진동자의 문제를 생각하면, 저항이 있는 단조화 진동자의 경우, $x_0, v_0$와 상관 없이 시간이 충분히 흐르고 나면 입자는 저항에 의해서 역학적 에너지를 잃고 $x = 0, v= 0 $의 상태에 도달하게 됩니다. 그리고 이 상태는 영원히 지속 됩니다. 즉,
$$\delta \gt 0 \Rightarrow \lim_{t \rightarrow \infty} x(t) = 0, \lim_{t \rightarrow \infty} v(t) = 0$$
입니다. 단조화 진동자 문제는 무한한 깊이의 우물이 하나 밖에 없기 때문에, 해가 단순합니다. 그러나 더핑 방정식의 우물은 두 개이기 때문에, $x_0, v_0$에 따라서 무한한 시간이 지났을 때, $x(t)$가 수렴하게 되는 값이 $1$ 혹은 $-1$의 두 가능성을 갖게 됩니다. 편의상 $x(t)$가 수렴하는 값을 $x_\infty$라고 하겠습니다.
위 예시와 같이 특정 동역학계에서 초기 상태와 상관 없이 무한히 긴 시간이 흘렀을 때, 수렴하게 되는 점을 끌개attractor라고 합니다. 끌개에는 여러 종류가 있으나, 위에서 설명한 "특정한 점으로 수렴하는 경우"는 고정점fixed point라고 합니다. 이번 포스팅에서는 고정점 형태의 끌개만을 다룰 것입니다. 따라서 끌개라는 용어와 고정점이라는 용어를 그냥 섞어서 사용하도록 하겠습니다. 끌개에는 고정점 뿐 아니라 다양한 종류를 갖습니다. 이에 대해서는 시간이 허락된다면 차차 포스팅을 하도록 하겠습니다.
역시나 생각하기 쉬운 예시인 $v_0 = 0$을 먼저 고려해 보겠습니다. $0 \lt x_0 \lt \sqrt{2}$ 라면, $x(t)$는 오른쪽 우물에서 진동하다가 $x = 1$에 수렴할 것 입니다. 만일 $x_0 \gt \sqrt{2}$ 라면, $x(t)$가 수렴하는 값은 구체적인 $x_0$의 값에 따라서 달라 집니다. 만일 $x_0$가 $\sqrt{2}$ 보다 조금 더 크다면, 입자는 $x = 0$ 근처로 올 때 까지 저항으로 인해 에너지를 많이 잃어서, 역학적 에너지가 음수가 될 수 있습니다. 이 경우에는 입자는 $x = 0$을 넘지 못 하고, $x_\infty = 1$이 됩니다. 그러나 초기 위치가 $\sqrt{2}$ 보다 더 커서, $x = 0$ 부근에 올 때 까지 역학적 에너지가 양수라면, 입자는 $x = 0$의 "언덕"을 넘을 수 있고, 왼쪽 우물로 갈 수 있습니다. 만일 $x = 0$의 언덕을 겨우 넘을 수 있을 정도의 역학적 에너지였다면, $x_\infty = -1$이 될 것 입니다. $x_0 \lt 0$ 인 경우에는 대칭성을 생각하면 됩니다. $x_0 = 0$ 이라면, 당연히도 $x_\infty = 0$ 이 됩니다. 따라서, $\delta \gt 0$ 인 경우, 고정점은 $x = -1, 0, 1$ 이렇게 3개가 존재합니다. 이 세 경우 모두 $v_\infty = 0$ 입니다. 따라서 좀 더 명확하게 하면 고정점은 $(-1, 0), (0, 0), (1, 0)$ 입니다.
$v_0 \gt 0$ 인 경우에는 초기 상태의 역학적 에너지를 생각하면 어떠한 고정점으로 수렴할 것인지를 파악할 수 있습니다.
끌림 영역basin of attraction
초기값 $(x_0, v_0)$에 따라 고정값은 $(-1, 0), (0, 1), (1, 0)$ 셋 중 하나가 결정되는데, 특정한 고정값에 대해서 그 고정값으로 수렴하게 되는 초기 상태들의 집합을 끌림 영역basin of attraction 이라고 합니다. 좀 더 명확하게 쓰면
$$B(x_\infty, v_\infty) = \{(x_0, v_0) | (x(t ; x_0, v_0), v(t ; x_0, v_0) \rightarrow (x_\infty, v_\infty) \}$$
입니다. 여기서 $x(t; x_0, v_0)$는 초기 상태가 $(x_0, v_0)$으로 주어졌을 때, 시간에 따른 상태를 의미 합니다. 더핑 방정식은 비선형 방정식으로 $(x(t), v(t))$를 해석적으로 구할 수 없기 때문에 끌림 영역 역시 해석적으로 구할 수 없습니다. 따라서 수치적인 방법을 써야 합니다.
수치 미분방정식 풀이를 통한 끌림 영역 구하기
수치 미분방정식을 통해 임의 초기 조건에 대해서 $(x(t), v(t))$를 구하고, 이로 부터 세 고정점에 대한 끌림 영역을 구해 보도록 하겠습니다. 고정점 $(0, 0)$는 자명하니, 제외 하도록 하겠습니다. 우선, 특수한 $(x_0, v_0)$에 대한 $(x(t), v(t))$를 구하면 아래와 같습니다.

$(x_0, v_0) = (1, 1)$에 대한 $(x(t), v(t))$ 의 궤적입니다. 초기에는 오른쪽 우물에서 시작했지만, 역학적 에너지가 충분하기 때문에, $x = 0$의 언덕을 넘어 왼쪽 우물로 가게 됩니다. 그런데, 저항으로 인해 역학적 에너지를 계속 잃어 왼쪽 우물의 고정점으로 수렴하게 됩니다. 즉, $(1, 1) \in B((-1, 0))$ 입니다. 물론 위 계산에서는 $t = \infty$ 까지 계산한 것은 아닙니다. 그러나, 직관으로 부터 $v(t)$가 매우 작을 때, $x(t)$가 놓여 있는 우물에 대응되는 고정점이 실제 고정점이 된다는 것을 알 수 있습니다.
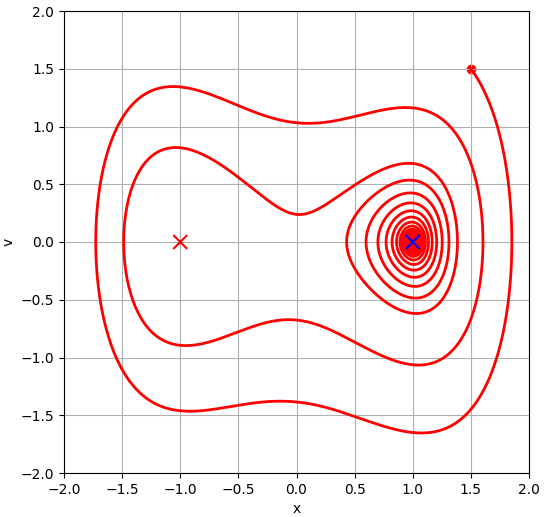
$(x_0, v_0) = (1.5, 1.5)$에 대한 $(x(t), v(t))$의 궤적입니다. 계산 결과로 부터 $(1.5, 1.5) \in B((1, 0))$ 임을 확인할 수 있습니다.

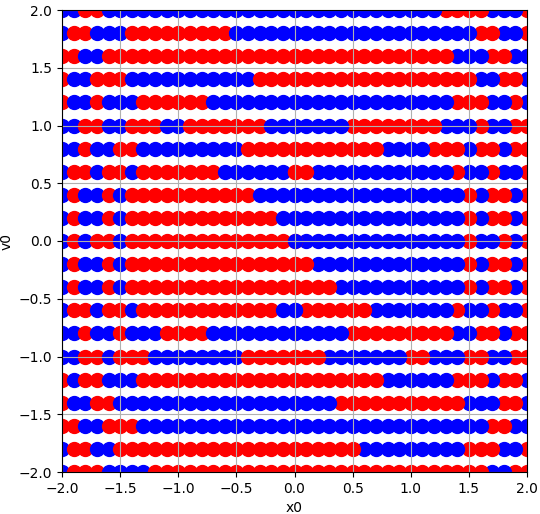
$[-2, 2] \times [-2, 2]$ 영역에 속한 각 점에 대응되는 고정점을 계산하면 결과는 위 그래프와 같습니다. $(x_0, v_0)$ 평면에 있는 각 점에 대해서 궤적을 구하고, 고정점을 찾아 낸 뒤, 고정점이 $(1, 0)$이라면 파란색으로, 고정점이 $(-1, 0)$이라면 붉은색으로 표시를 하였습니다. $(x_0, v_0) \approx (1, 0)$ 이라면, 고정점은 $(1, 0)$이 됩니다. 이는 다소 자명한 결과 입니다. $(x_0, v_0)$이 각 고정점 혹은 원점에서 많이 떨어져 있다면, 고정점은 $(x_0, v_0)$의 정확한 위치에 따라 달라집니다.
위 그래프는 영역을 $21 \times 21$개의 공간으로 나누어 총 441개의 $(x_0, v_0)$에 대한 궤적을 구하고, 이를 통해 고정점을 얻었습니다. 그런데 441 개로만 하니 좀 성들다는 느낌이 듭니다. 그래서 좀 더 빼곡하게 공간을 채우고 싶습니다. 그런데, 그렇게 하려면 적어도 $100 \times 100$ 정도로 공간을 나누어야 할 것이고, 이 경우에는 총 10,000개의 시작점에 대한 계산을 해야합니다. 계산량이 무척이나 큽니다. 수학적, 물리적 직관 혹은 성질을 이용하여 끌림 영역을 좀 더 효율적으로 계산할 수는 없을까요?
공간의 대칭성 이용하기
만일 $(x_0, v_0)$가 $(x_\infty, 0)$으로 수렴한다고 하겠습니다. 그러면, $(-x_0, -v_0)$는 어디로 수렴을 하게 될까요? 조금만 생각을 해 보면 $(-x_\infty, 0)$로 수렴을 한다는 것을 알 수 있습니다. 따라서, $(x_0, v_0)$에 대한 계산을 하면, $(-x_0, -v_0)$에 대한 계산을 할 필요가 없게 됩니다. 이는 우리의 문제가 공간 대칭성을 갖고 있기 때문입니다. 정확히 수식을 써서 이를 보이자면, $(x', v') = (-x, -v)$와 같이 $(x', v')$를 정의 했다고 하겠습니다. 이는 위치와 속도의 부호를 바꾸는 것 입니다. $(x', v')$에 대한 미분방정식을 쓰면,
$$-\dot{x'} = -v'$$
$$-\dot{v'} = -\alpha (-x') - \beta (-x')^3 - \delta (-x')$$
이 되고, 이를 정리하면,
$$\dot{x'} = v'$$
$$\dot{v'} = -\alpha x' - \beta x'^3 - \delta x'$$
이 됩니다. 이는 $(x, v)$가 만족해야 하는 미분 방정식과 동일합니다! 즉, $(x(t), v(t))$가 미분 방정식의 해라고 한다면, $(x'(t), v'(t)) =(-x(t), -v(t))$ 역시 미분 방정식의 해가 된다는 뜻 입니다. 따라서, $(x_0, v_0)$가 $(x_\infty, 0)$으로 수렴한다면, $(-x_0, -v_0)$는 $(-x_\infty, 0)$으로 수렴하게 됩니다. 앞에서 직관에 의존했던 결과를 증명한 것 입니다.
이 성질로 부터 계산량을 반으로 줄일 수 있습니다. 혹은 동일한 계산량으로 두 배로 많은 점을 계산할 수 있습니다. 제 1, 4 사분면의 점에서 고정점을 계산하고, 이를 원점 대칭 이동시키면, 제 2, 3 사분면의 점에서의 고정점을 구할 수 있는 것 입니다. 이 성질을 이용하여 계산을 하면,
결과는 위와 같습니다. 대칭성을 이용하지 않았을 때와 계산량은 동일한데, 공간의 점의 밀도는 2배 증가하였습니다. 위 그래프에서는 $x$ 축 방향의 밀도가 $v$축 방향의 밀도보다 2배 높습니다. 이렇게 그림을 그리면 이쁘지 않으니, $v$축 방향의 밀도를 2배 높이도록 하겠습니다.
결과는 위 그래프와 같습니다. 위 결과는 다음과 같이 설명할 수 있습니다. 우선, $(x_0, v_0)$가 각 고정점 근처라면, $(x_0, v_0)$는 가까운 고정점에 대응되는 끌림영역의 원소가 됩니다. "가까운"에 대해서 좀 더 명확하게 설명하자면, $delta = 0$인 경우 앞에서 이미 설명한 바와 같이, 역학적 에너지가 음수인 경우에는 초기에 속했던 우물을 빠져 나갈 수 없이, 그 우물에서 진동하게 됩니다. $\delta \gt 0$인 경우에는 역학적 에너지를 잃고 결국에는 고정점으로 수렴하게 되는데, 따라서 $(x_0, v_0)$의 역학적 에너지가 음수라면, $(x_0, v_0)$는 이 우물에 속한 고정점에 대응되는 끌림영역의 원소가 됩니다.
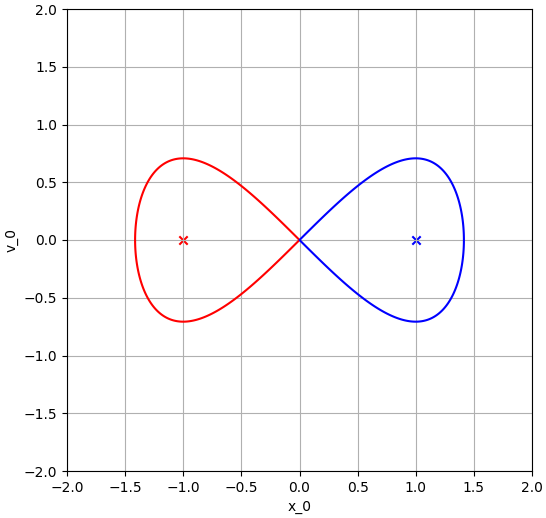
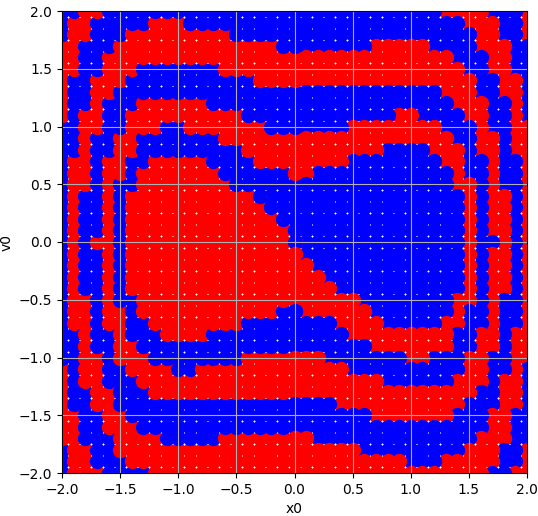
위 그래프는 $(x, v)$ 공간에서 역학적 에너지가 0이 되는 등고선을 표현한 것 입니다. 각 X 는 고정점을 의미 하는데, 따라서 $(x_0, v_0)$가 등고선 안쪽에 놓여 있다면, 이 점은 시간의 흐름에 따라 같은 등고선의 안쪽에 있는 고정점으로 수렴하게 되고, 따라서 등고선의 안쪽 영역은 해당 고정점의 끌림 영역의 부분집합이 됩니다. 수치적으로 계산한 끌림 영역의 그래프는 이 설명에 부합됩니다. $(x_0, v_0)$의 역학적 에너지가 커진다면, 입자는 왼쪽 오른쪽 우물을 진동할 것이고, 구체적인 초기 역학적 에너지의 값에 따라서 수렴하는 고정점이 정해질 것 입니다. 그래서 위 수치적으로 계산한 끌림 영역의 형태가 되게 됩니다.
더핑 방정식의 끌림 영역 ($\alpha = -1, \beta = 1,\delta = 0.1$)
효율적인 방법을 사용하여 정확한 끌림 영역을 그리면 그 결과는 아래와 같습니다.
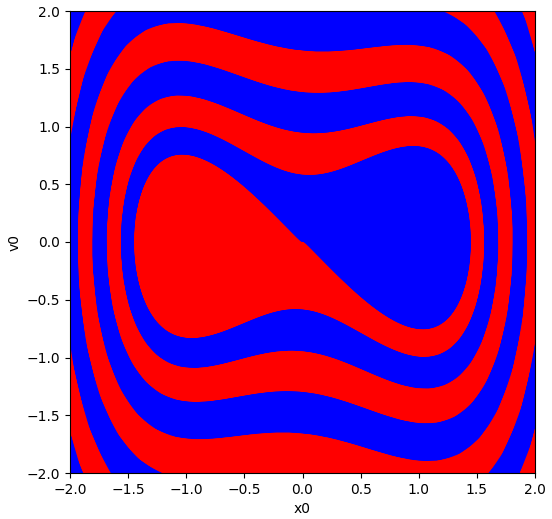
다시 한 번 설명 하면, $(x_0, v_0)$가 파란색 영역에 속해 있다면, 초기값이 $(x_0, v_0)$인 상태는 더핑 방정식에 따라서 시간이 무한히 흐른 뒤 $(1, 0)$으로 수렴하게 됩니다. 반대로 $(x_0, v_0)$가 빨간색 영역에 속해 있다면, 초기값이 $(x_0, v_0)$인 상태는 더핑 방정식에 따라서 시간이 무한히 흐른 뒤 $(-1, 0)$으로 수렴하게 됩니다.
위 그래프는 앞에서 구한 그래프에 비해서 빈틈이 없이 매우 빽빽하게 $(x_0, v_0)$의 공간을 채우고 있습니다. 실제로 모든 $(x_0, v_0)$에 대해서 $(x(t), v(t))$를 구한 것은 아니고, 더핑 방정식의 수학적, 물리학적 성질을 활용하여 효율적인 방법으로 구한 것 입니다. 이에 대해서는 다음 포스팅에서 알아 보도록 하겠습니다.
'수학' 카테고리의 다른 글
| [수학적 최적화] 경사 하강법Gradient Descent(혹은 Steepest Descent) 알아 보기 : (1) 기본 개념 (1) | 2023.05.29 |
|---|---|
| 타원 상의 한 점과 타원 밖의 한 점 사이의 거리 구하기 (1) | 2023.05.12 |
| [수학적 최적화] 시뮬레이션 담금질 Simulated Annealing을 활용한 외판원 문제 Travelling salesman problem 문제 풀기 (0) | 2023.05.10 |
| [수학적 최적화] 시뮬레이션 담금질 Simulated Annealing의 이해와 파이썬 코드 (2) | 2023.05.06 |
| 포물선의 반사의 성질 : 축에 나란한 방향으로 입사한 빛은 반드시 포물선의 초점을 지난다 (3) | 2023.04.06 |



