타원 상의 한 점과 타원 밖의 한 점 사이의 거리 구하기

이번 포스팅은 다소 간단한 내용을 담고 있는 포스팅인데, 제가 실제로 하고 있는 없무와 약간 관련성이 있기 때문에 하는 포스팅입니다. 

 

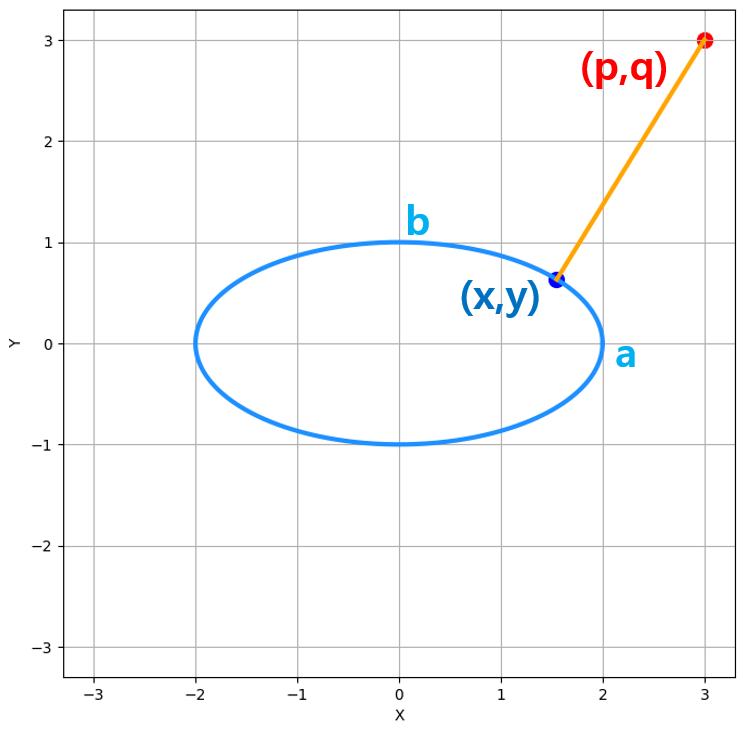
문제는 타원과 타워 밖의 한 점이 주어져 있을 때, 타원과 점 사이의 거리를 구하는 것 입니다. 문제를 최대한 간단하게 하기 위해서 2차원 공간을 생각하겠습니다. 2차원 공간에서 타원의 방정식은 

$$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$$

로 주어집니다. 타원 위의 일반적인 점을 $\overrightarrow{x}=(x,y)$라 놓겠습니다. 타원 밖의 한 점의 좌표를 $\overrightarrow{p}=(p,q)$ 라고 하겠습니다. 이 점은 타원의 밖에 있습니다. 일반화를 잃지 않고 타원과 타원 밖의 점의 배치를 위 그림과 같이 놓을 수 있습니다. 타원의 중심이 원점이 아니라면, 평행 이동을 통해 타원의 중심을 원점으로 놓을 수 있습니다. 타원의 축 방향이 X, Y 축과 나란하지 않다면 좌표 회전을 통해서 타원의 축 방향이 X, Y 축과 나란하게 놓을 수 있습니다 .또한 점 $(p,q)$가 제 1사분면에 놓여 있지 않은 경우,  X축 훅은 Y축을 기준으로 거울 반사 이동 시켜서 제 1사분면에 놓을 수 있습니다. 평행이동, 회전 변환, 거울 반사 이동은 점과 점 사이의 거리를 보존하는 변환이기 때문에, 이와 같은 변환을 하더라도 문제의 정답은 전혀 달라지지 않습니다. 

 

우리 문제는 $d(\overrightarrow{x})=|\overrightarrow{x}-\overrightarrow{p}|$를 최소화하는 타원 위의 점 $\overrightarrow{x}$를 찾는 것 입니다. 좀 더 명확하게 수학적으로 표현하면,

$${\overrightarrow{x}}_{\text{opt}}=\arg min|\overrightarrow{x}-\overrightarrow{p}|,\text{ subject to }\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$$

입니다. 매우 단순한 형태의 구속 조건이 있는 하의 최적화 문제 입니다. 

 

1. 타원 상의 점을 매개변수화를 이용한 풀이

 

(가장?) 간단하게 이 문제에 접근 할 수 있는 방법은 타원 상의 점을 매개변수화 하여 표현하고, $|\overrightarrow{x}-\overrightarrow{p}|$ 를 매개변수로 표현하고, 이를 매개변수로 미분하여 미분이 0이 되는 값을 찾는 것 입니다. 타원상의 점은 $\theta =[0,2\pi ]$라 했을 때,

$$x=a\cos \theta$$

$$y=b\sin \theta$$

으로 표현할 수 있습니다. 따라서 $d(\overrightarrow{x})=d(\theta )=\sqrt{(a\cos \theta -p{)}^2+(b\sin \theta -b{)}^2}$ 가 됩니다. $d(\theta )$는 표현식에 근호가 있어 복잡하니 이를 제곱한 값을 사용하도록 하겠습니다. 즉, $f(\theta )=d(\theta {)}^2=(a\cos \theta -p{)}^2+(b\sin \theta -b{)}^2$ 라고 놓고, 

$$\frac{df}{d\theta }=0$$

이 되게 하는 $\theta$를 찾으면 됩니다.

$$\frac{df}{d\theta }=-2a\sin \theta (a\cos \theta -x)+2b\cos \theta (b\sin \theta -y)$$

인데, $\cot \theta$를 $t$라고 놓으면, $\sin \theta =\sqrt{1-t^2}$이 되고(물론 $\pm$ 부호가 앞에 붙어야 하지만, 양수만을 채택 하도록 하겠습니다. 그 이유는 나중에 설명합니다), 위 식을 $t$에 대해서 정리하면,

$$f(t)=-2a\sqrt{1-t^2}(at-x)+2bt(b\sqrt{1-t^2}-y)$$

가 됩니다. $f(t)=0$을 구해야 하는 것이 목적이니, 이는 

$$\sqrt{1-t^2}(t(-a^2+b^2)+at)=bty$$

와 같고, 루트를 없애기 위해서 양변을 제곱하여 정리하면,

$$(1-t^2)\{t(-a^2+b^2)+ax{\}}^2-b^2{y}^2{t}^2=0$$

이 됩니다. 이 식을 $t$에 대해서 정리하면,

$$-(a^2-b^2{)}^2{t}^4+2ax(a^2-b^2)t^3+\{a^4-a^2(2b^2+x^2)+b^4-b^2{y}^2\}{t}^2+2ax(b^2-a^2)t+a^2{x}^2=0$$

와 같이 $t$에 대한 4차 방정식이 됩니다. 4차 방정식은 근의 공식이 있어서 이 식을 해석적으로도 풀 수 있습니다. 

 

$t=\cos \theta$ 라고 두었고, $\overrightarrow{p}$는 제 1사분면에 있기 때문에 $\cos \theta$는 양수이며, $\sin \theta$ 역시 양수가 됩니다. 따라서 위 4차 방정식의 해 중에서, 양수이면서 0보다 크거나 같고 1보다 작거나 같은 $t$에 해당하는 값이 우리가 찾는 $\cos \theta$ 값이 됩니다. 이 조건을 만족 시키는 4차 방정식의 해를 $t_0$ 이라고 놓으면, 

$$x=a{t}_0,y=b\sqrt{1-t_0^2}$$

가 우리가 찾는 최종 해가 됩니다. 4차 방정식의 해를 해석적으로 쓰면 너무 길어지기 때문에, 그냥 $t_0$로 놓고 더 이상 풀어쓰지 않도록 하겠습니다. 

 

이 방법은 직관적이면서 간단한 방법이지만, 공간의 차원이 높아진다면 시도하기 어려운 방법입니다. 예를들어, 같은 문제를 3차원 공간에서 푼다면, 타원을 표현하기 위한 매개변수는 2개가 필요합니다. 예를들어 구면 좌표계와 같은 변환을 사용하면, $$\frac{x^2}{a^2}+\frac{y^2}{b^2}+\frac{z^2}{c^2}=1$$

를 기술하는 매개 변수화는

$$x=a\sin \theta \cos \varphi$$

$$y=a\sin \theta \sin \varphi$$

$$z=a\cos \theta$$

이 있습니다. 이를 이용하면 $|\overrightarrow{x}-\overrightarrow{p}|$는 $\theta ,\varphi$의 함수가 됩니다. $\theta ,\varphi$에 대한 연립 방정식을 풀어야 하는데, 이 과정이 어려울 수 도 있습니다. 그나마 공간 차원이 3차원이면 그런대로 식이라도 전개할 수 있는데, 일반적으로 $n$ 차원 공간에서의 문제를 풀려고 하려면 한도 끝도 없이 식이 복잡해 지고, 결국에는 문제를 풀 수 없어 집니다.

 

2. 라그랑지 승수를 이용한 풀이

 

구속 조건이 있는 최적화 문제라면 라그랑지 승수Lagrange multiiplier를 이용하여 최적화 문제를 해결 할 수 있습니다. 위 문제에 대한 라그랑지안은

$$\mathcal{L}=|\overrightarrow{x}-\overrightarrow{p}{|}^2-\lambda (\overrightarrow{x}\mathrm{\Sigma }\overrightarrow{x}-1)$$

입니다. 여기서 $\lambda$는 라그랑지 승수 입니다. 

$$\mathrm{\Sigma }=\left(\begin{array}{cc}\frac{1}{a^2}& 0\\ 0& \frac{1}{b^2}\end{array}\right)$$

입니다. 따라서 $\overrightarrow{x}\mathrm{\Sigma }\overrightarrow{x}-1$ 를 풀어서 쓰면, 타원의 방정식 $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$이 됩니다. 2차 형식의 경우 위와 같이 $\mathrm{\Sigma }$ 행렬을 사용하면 간단하게 표현할 수 있습니다. 위 라그랑지안에 대한 최적화 해는

$$\frac{\partial \mathcal{L}}{\partial \overrightarrow{x}}=2(\overrightarrow{x}-\overrightarrow{p})-2\lambda \mathrm{\Sigma }\overrightarrow{x}=0$$

$$\frac{\partial \mathcal{L}}{\partial \lambda }=\overrightarrow{x}\mathrm{\Sigma }\overrightarrow{x}-1=0$$

을 동시에 만족하는 $\overrightarrow{x},\lambda$ 입니다. 첫 번째 식을 $\overrightarrow{x}$에 대해서 정리하면, 

$$\overrightarrow{x}=(1-\lambda \mathrm{\Sigma }{)}^{-1}\overrightarrow{p}$$

가 되고, 이를 두 번째 식에 대입하여 정리하면

$$f(\lambda )=(1-\lambda \mathrm{\Sigma }{)}^{-1}\overrightarrow{p}\mathrm{\Sigma }(1-\lambda \mathrm{\Sigma }{)}^{-1}\overrightarrow{p}-1=0$$

이 됩니다. 위 식에서 $\mathrm{\Sigma },\overrightarrow{p}$는 이미 주어진 값이니, 위 식은 $\lambda$에 대한 방정식이 됩니다. 이 $\lambda$에 대한 해를 ${\lambda }_0$이라고 하면, 우리가 찾고자 하는 해는 $\overrightarrow{x}=(1-\lambda \mathrm{\Sigma }{)}^{-1}\overrightarrow{p}$ 가 됩니다. 위 식에서 나오는 행렬은 모두 $2\times 2$ 행렬이기 때문에 역행렬을 해석적으로 구할 수 있습니다. 그런데 전체 식은 $\lambda$에 대한 조금은 복잡한 식이 되니, 이를 해석적으로 계산을 할 수는 있으나 조금은 어렵고 귀찮습니다. 

 

이런 경우에는 위 $f(\lambda )$의 해를 수치적인 방법으로 구할 수 있습니다. 아래는 $\lambda$를 계산하고, 최종적으로는 $\overrightarrow{x}$를 계산하는 파이썬 코드 입니다.

import numpy as np
from scipy import optimize

def function(lam):
    A = np.identity(2) - lam* sigma
    Ainv = np.linalg.inv(A)
    y = np.matmul(Ainv, x)
    f = y.transpose() @ sigma @ y-1
    return f

def return_p(lam):
    A = np.identity(2) - lam * sigma
    Ainv = np.linalg.inv(A)
    y = np.matmul(Ainv, x)
    return y


def lagrangian():
    a, b = 2, 1
    x = np.array([5, 5])

    sigma = np.zeros([2, 2])
    sigma[0, 0] = 1 / a ** 2.0
    sigma[1, 1] = 1 / b ** 2.0

    sol = optimize.brentq(function, -1e8, 0)
    p1 = return_p(sol)
    return p1

if __name__ == '__main__':
	lagrangian()

위 코드에서는 scipy의 라이브러리인 optimize.brentq 알고리듬을 활용합니다. 

 

이 방식은 다로 복잡해 보이기는 하지만, 일반적인 공간 차원에서의 문제를 풀 수 있다는 장점이 있습니다. 위에서 문제를 설명하기 위해서 $\mathrm{\Sigma }$를 $2\times 2$ 행렬로 두었지만, 일반적인 $n$차원 공간의 문제는 $\mathrm{\Sigma }$가 $n\times n$ 행렬로 바뀌는 것 밖에는 차이가 없습니다. 코딩을 해 둔다면 숫자만 몇 개 더 넣으면 해결되는 문제 입니다.