기각 샘플링 기반 몬테 카를로 적분이 부정확한 예시
지난 시간에 소개한 기각 샘플링 방법을 통해서
$$A = \int_{-\infty}^{\infty} x^2 \frac{1}{\sqrt{2 \pi}} e^{-\frac{x^2}{2}}dx$$
을 해 보도록 하겠습니다. $f(x) =x^2 \frac{1}{\sqrt{2 \pi}} e^{-\frac{x^2}{2}}$라 할 때, $\frac{1}{\sqrt{2 \pi}} e^{-\frac{x^2}{2}}$ 는 우리가 잘 알고 있는 표준 정규 분포의 함수 이므로, 편의상 $N(x)$라고 표시한다면, $f(x) = x^2 N(x)$ 가 됩니다. 적분의 상한과 하한은 $\infty, -\infty$인데 무한대를 다루기는 어려우니 상한과 하한을 각각 20, -20 정도로 제한하여 실제로
$$A = \int_{-20}^{20} x^2 \frac{1}{\sqrt{2 \pi}} e^{-\frac{x^2}{2}}dx$$
을 계산해 보도록 하겠습니다.
이 값은 해석적으로 계산이 가능하고 그 값은 정확히 1 입니다. 계산 과정은 지난 두 번의 포스팅에서 자세히 설명 했기에, 그래프를 통해서 간단히 소개하도록 하겠습니다.

적분 영역 (-20, 20)과 함수의 최대 최소를 포함하는 사각형을 잡아야 하는데, 함수의 최대값은 그래프를 그려 보면 0.3 보다 작다는 것을 알 수 있습니다. 따라서 이번 계산에서 $W = 40 = 20 - (-20), H = 0.3$ 으로 선택했습니다. 위 그래프는 $N = 1,000$ 개의 기각 샘플링을 통해서 얻은 결과 인데요, 적분 영역에 속해 있는 점은 하늘색, 그렇지 않은 점은 빨간색으로 표시하였습니다. 최종 결과는 $A = 1.104$, 에러는 $error = 0.104$가 됩니다. 에러는 10.4%로 생각보다 꽤나 큽니다.
지난 포스팅에서 예제로 들었던 함수의 적분에 비해서, 이번 함수의 적분 계산 과정의 그래프를 보면 전체 샘플링 대비 적분 영역에 속하는 샘플링 포인트의 갯수가 매우 적다는 것을 확인할 수 있습니다. 원주율을 구하거나, 간단한 함수의 적분을 구한 지난 포스팅에서는 대략적으로 하늘색 : 빨간색 점의 비율이 1:1 수준이었는데, 이번 문제의 경우엔, 사각형의 넓이가 $H \cdot W = 40 \cdot 0.3 = 12$ 이고 적분 영역의 넓이가 $1$ 이니, 비율은 $1:12$ 가 됩니다. 즉, 기각 샘플링을 통해 전체 샘플링 포인트의 $\frac{11}{12}$ 는 기각(빨간색)이 되는 것 입니다.
기각의 비율이 너무 높습니다. 이 경우 최종 결과값이 계산을 실행할 때 마다 크게 다르게 나온다는 것을 실제 시뮬레이션을 해 보면 알 수 있습니다. 실제로 위 계산을 10번 반복한 시행에서
$0.972, 0.792, 1.188, 1.032, 0.768, 1.008, 1.14, 0.78, 0.96, 0.963$
을 얻었고, 이 값의 평균과 표준편차는 각각 $m = 0.9576, \sigma = 0.1378$이 됩니다. 굉장히 큰 값 입니다. 물론 샘플링의 횟수를 크게 한다든가 혹은 계산을 여러번 반복하여 평균을 취하면 참값인 1.0에 가까워 질 수 있겠지만, 만일 실제 활용에서는 여러번 계산을 하기 힘든 정도로 복잡한 계산이거나 계산 시간이 오래 걸리는 계산이라면 몇 번의 계산 밖에 하지 못 할 것 입니다. 단 한 번의 계산 밖에 하지 못 한다면, 극단적인 경우 위에서와 같이 0.768이나 1.118 처럼 참값과 매우 차이가 큰 결과가 얻어질 수 도 있습니다.
이처럼 계산을 실행할 때 마다 그 결과 값이 다르게 나오는 것은 무작위성에 기초를 둔 몬테 카를로 적분 더 넓게는 몬테 카를로 시뮬레이션 전반의 어쩔 수 없이 피할 수 없는 단점이 됩니다. 계산을 할 때 마다 답이 다르게 나온다는 것은 답의 분포의 분산이 매우 크다는 것 인데요, 따라서 이 분산을 줄일 수 있는 다양한 방법이 고안되어 왔습니다. 이번 포스팅에서는 간단하면서도 활용이 많은 방법 중 하나인 메트로폴리스-헤이스팅스(Metropolis-Hastings) 샘플링을 통한 몬테 카를로 적분 방법에 대해 알아 보도록 하겠습니다. 기존 기각 샘플링을 메트로폴리스-헤이스팅스 샘플링 기법으로 교체하여 어떻게 계산의 분산을 줄일 수 있는지를 중점적으로 확인할 것 입니다.
기각 샘플링의 경우, 왜 적분값의 분산이 컸나?
지난 포스팅에서 설명한 바와 같이 기각 샘플링의 경우, 적분 영역에 속하는 샘플링 포인트의 갯수는 이항 분포(Binomial distribution)를 따릅니다. 기각 샘플링의 횟수를 $N$, 전체 사각형 영역에서 적분 영역에 속하는 영역의 넓이 비율을 $p$라고 하면, 적분 영역에 속하는 샘플링 포인트의 갯수 $N_{in}$은 $N_{in} ~ B(N, p)$라고 쓸 수 있습니다. $B$는 이항 분포를 나타 냅니다. 이항 분포의 경우 평균은 $m = Np$, 표준 편차는 $\sigma = \sqrt{Np(1-p)}$가 됩니다. 평균 값 대비 표준 편차의 비율은
$$\frac{\sigma}{m} = \frac{\sqrt{Np(1-p)}}{Np} = \sqrt{\frac{(1-p)}{Np}}$$
가 됩니다.
이번 포스팅의 경우와 같이, $p$가 작은 경우에는 위 $\frac{\sigma}{m}$이 매우 커지기 때문에, 계산을 할 때마다 계산 결과가 크게 달라진 것 입니다. 즉 이전 두 포스팅의 경우에서 처럼, 샘플링을 하는 사각형의 넓이 대비 적분 영여의 넓이가 커야, 즉 $p$ 값이 커야, 계산 결과의 변화가 작아 집니다. 하지만 일반적인 경우에는 함수의 개형에 따라서 이 $p$값이 항상 작은 값을 가질 수 도 있고, 사각형의 높이$H$를 적당히 잡아 주지 못 한다면 $p$값이 역시 매우 작아 질 수 도 있습니다. 이번 포스팅에서는 $f(x)$의 최대값이 0.3 보다는 작다는 것을 그래프를 통해서 쉽게 알 수 있었지만, 일반적인 경우에는 함수의 정의역이 고차원이거나 함수의 최대값을 쉽게 알 수 없다면 $H$값을 매우 크게 설정해야 하는데요, 이 경우엔 $p$값이 작아질 수 밖에 없습니다. 즉, 기각 샘플링은 몬테 카를로 적분의 개념을 설명하고 간단한 문제를 계산하는데는 매우 좋은 샘플링 기법이지만, 매우 일반적인 경우에는 적당하지 않은 샘플링 입니다.
적분하려는 함수에 적합한 샘플링을 할 수 없을까?
위에서 언급한 문제 외에도, 기각 샘플링이 이번 문제에 적합하지 않은 이유가 하나 더 있습니다. 적분 영역은 $(-20, 20)$ 이지만, 적분에 기여하는 영역은 (-5, 5) 정도로 전체 적분 영역에서 매우 좁은 구간이라는 것 입니다. $f(x) = x^2 N(x)$ 에서 $N(x)$는 $x=0$에서 멀어질수록 급격히 작아지는데, 대부분의 적분값은 $-5<x<5$에서 정해지고, $x>5$ 혹은 $x<-5$ 영역에서의 적분 기여는 거의 없습니다. 따라서 적분값을 정확하고 효율적으로 계산하기 위해서는 $-5<x<5$ 구간에서는 샘플링을 많이하고, $x>5, x<-5$ 영역에서는 샘플링을 거의 하지 않아도 됩니다.
메트로폴리스-헤이스팅스 샘플링은 위와 같이 함수값이 크고 급격하게 변하는 구간에서는 촘촘한 샘플링을, 함수값이 0에 가까워서 적분에 기여가 거의 없는 구간에서는 성글게 샘플링을 하는 샘플링 기법입니다. 피적분함수 $f(x)$의 성질을 이용하기 때문에 임의의 $x$에 대해서 $f(x)$를 계산해야 하지 않을까? 하는 걱정이 생길 수 도 있는데(이 경우 계산량이 커지게 됩니다), 다행이도 임의의 $x$에 대해서 $f(x)$를 완벽히 계산하지 않아도 된다는 상당한 장점이 있습니다.
피적분함수 $f(x)$를 조금 다르게 써 보자
이번 문제의 피적분함수 $f(x)$를 우리는 이미 $f(x) = x^2 N(x)$ 와 같이 두 함수의 곱으로 표현해 왔습니다. 그리고 $N(x)$는 모든 $x$에 대해서 양수이며, $N(x)$를 전구간에서 적분한 값이 1이 된다는 사실도 알고 있습니다. 따라서 피적분함수를 $f(x) = \frac{f(x)}{N(x)}N(x)$와 같이 쓸 수 있으며, 구하려는 적분값은 $A = \int f(x)dx = \int \frac{f(x)}{N(x)}N(x)dx$ 처럼 쓸 수 있습니다. 마지막 식은 또 한 번 바꿔서 쓸 수 있는데, $\frac{dM(x)}{dx} = N(x)$를 만족하는 $M(x)$가 있을 때,
$$A =\int_{x_{min}}^{x_{max}} \frac{f(x)}{N(x)}N(x)dx = \int_{x_{min}}^{x_{max}} \frac{f(x)}{N(x)} M'(x)dx = \int_{M(x_{min})}^{M(x_{max})} \frac{f(x)}{N(x)} dM(x)$$
와 같이 쓸 수 있습니다. 마지막 등호에서는 치환적분을 한 것이며, $N(x)$가 항상 양수인 함수이기 때문에, $M(x)$는 증가 함수이고, 따라서 $dM$ 적분의 범위는 간단히 $[M(x_{min}), M(x_{max})]$가 됩니다. $N(x)$는 정규 분포 함수이므로
$$M(x) = \int_{-\infty}^{x} N(t) dt$$
가 됩니다. $M$의 영력은 $[0, 1]$가 됩니다.
마지막 적분식을 다시 한 번 쓰면,
$$A = \int_{M(x_{min})}^{M(x_{max})} \frac{f(x)}{N(x)} dM(x) = \int_{M(x_{min})}^{M(x_{max})} \frac{f}{N}(M) dM$$
와 같이 완전히 $M$에 대한 함수로 쓸 수 있습니다. 앞서 설명한 바와 같이 $M(x)$는 단조 증가 함수이기 때문에 역함수인 $M^{-1}(x)$가 존재하고 이를 통해서 $x \rightarrow M$으로 변환이 가능합니다.
최종적으로 구해야 하는 적분은 $M$에 대한 적분이며, 이 적분을 $M$의 공간에서 구분구적법을 통해서 구할 수 있습니다. $M$ 공간에서 구분구적법은
$$A = \lim_{K \to \infty} \frac{1}{K} \sum_{n=1}^{K} \frac{f}{N}(M_n) \Big(M(x_{min}) - M(x_{max})\Big) $$
이고, $M_n$은 $M$를 $[M(x_{min}), M(x_{max})]$ 구간에서 균등하게 나눈 $n$번째 $M$ 값 입니다. $\frac{f}{N}(M_n)$의 계산은 실제로는 $M_n$에 대응되는 $x$를 구하고, 이를 이용하여 $\frac{f(x)}{N(x)}$를 해 주어야 합니다. 즉, 이번 문제의 경우 $\frac{f(x)}{N(x)} = x^2$가 됩니다.

그러면, 문제는 $M$공간에서 균등한 값의 집합인 $\{ M_n | n = 1, 2, 3, ... \}$은 $x$ 공간에서는 어떤 집합 $\{ x_n | n = 1, 2, 3, ... \}$ 이 될 것 인가? 인데요, 이는 $M(x)$의 그래프를 한 번 그려보면 직관적으로 그 답을 얻을 수 있습니다.
위 그래프의 하늘색 점은 $y=M(x)$위에 $M$ 공간 [0, 1]에서 균등하게 20조각으로 나누고, 각 $M$ 값에 해당되는 점을 그래프 상에서 찍은 것 입니다. 주황색 점은 하늘색 점의 $x$좌표 점이 됩니다. 즉, $M$ 공간에서 균등 분포는 $x$공간에서는 0 근처에 밀도가 높은 분포에 해당합니다. 연속되는 하늘색 점의 $x$좌표의 차이는 $y = M(x)$그래프의 기울기에 반비례 하게 되므로, 연속되는 주황색 점의 값의 차이는 $\frac{1}{M'(x)}$에 비례합니다. 연속적인 두 점의 거리가 $\frac{1}{M'(x)}$에 비례하게 되면, 점의 분포는 $M'(x)$에 비례함을 알 수 있고, 따라서 $x$의 분포는 $M'(x) = N(x)$값에 비례하게 됩니다.
즉, 설명이 좀 길긴 했지만 그리 어렵지 않게 이해할 수 있는데, $M$ 공간에서 균등한 분포는 $x$ 공간에서는 $N(x)$의 분포를 따르게 됩니다.
따라서,
$$A = \lim_{K \to \infty} \frac{1}{K} \sum_{x_n \sim N(x), n=1}^{K} \frac{f(x_n)}{N(x_n)}$$
와 같이 완전히 $x$에 대한 식으로 다시 쓸 수 있습니다. 여기서 $x \sim N(x)$는 $x$가 확률 밀도 함수 $N(x)$를 따르는 샘플링을 뜻 합니다. 이 마지막 식은 확률 밀도 함수 $N(x)$에 대한 $\frac{f(x)}{N(x)}$의 평균을 정의하는 식과 정확히 같기 때문에,
$$A = E(\frac{f(x)}{N(x)}, N(x)) = E(x^2, N(x)) = \langle x^2 \rangle _{N(x)}$$
이 됩니다. $\langle x^2 \rangle _{N(x)}$는 확률 밀도 함수 $N(x)$를 따르는 확률 변수 $x^2$의 평균을 뜻 합니다.
위 과정을 일반화 한다면, $f(x)$와 $p(x)>0, \int p(x) dx = 1$ 인 $p(x)$ 에 대하여,
$$ \int f(x) dx = \int \frac{f(x)}{p(x)} p(x) dx = E\Big(\frac{f(x)}{p(x)}, p(x)\Big) = \Big \langle \frac{f(x)}{p(x)} \Big \rangle _{p(x)} $$
가 됩니다.
이제 남은 것은 $N(x)$를 따르는 $x$의 집합(분포) $\{x_i | i =1, 2, 3, ... K\}$를 생성하는 것 입니다. 그 다음은 각 $x_i$에 대해 $\frac{f(x_i)}{N(x_i)}$를 계산하여 $\{\frac{f(x_i)}{N(x_i)}| i =1, 2, 3, ... K\}$를 얻고, 이것들의 평균을 구하면 됩니다. 이 과정은 단순한 산수입니다.
특정한 분포를 따르는 샘플링 하기 : 메트로폴리스-헤이스팅스 알고리듬
드디어, 이번 단락 부터 이번 포스팅의 주제인 메트로폴리스-헤이스팅스 알고리듬에 대해서 이야기 할 수 있습니다! 앞의 내용은 기각 샘플링이 적절할 샘플링이 아닐 수 있다는 것을 알아 보았고, 또한 구하려는 적분값은 피적분 함수를 잘 변형하면, 특정 확률 밀도 함수를 따르는 확률 변수의 평균으로 취급할 수 있다는 것 이었습니다. 이 두 가지를 정확히 이해해야 메트로폴리스-헤이스팅스 알고리듬이 왜 도입되어야 하고, 어떠한 의미를 갖는지를 알 수 있기 때문입니다.
메트로폴리스-헤이스팅스 알고리듬은 특정 확률 밀도 함수를 따르는 확률 변수의 분포를 생성하는 알고리듬 입니다. 이번 포스팅의 문제로 국한시킨다면 확률 밀도 함수 $N(x)$를 따르는 $x$의 분포를 만들어 내는 방법입니다. (이번 포스팅의 문제에서 $N(x)$는 표준 정규 분포인데, 사실 표준 정규 분포를 따르는 샘플링은 굳이 메트로폴리스-헤이스팅스 알고리듬을 통해서 할 필요는 없고, 표준 정규 분포의 샘플링에 특화된 다른 알고리듬을 사용하는 것이 더 좋습니다. 마치 닭을 잡는데 소 잡는 칼을 사용한 겪인데, 포스팅의 목적이 효율적인 샘플링이 아니라 메트로폴리스-헤이스팅스 알고리듬을 설명하는 것이기 때문에, 이 같은 우려는 하지 않아도 될 것 입니다) $N(x)$를 따르는 분포이니, $N(x)$값이 큰 곳에는 $x$가 많이 샘플링 될 것이고, $N(x)$값이 작은 곳에서는 $x$가 성글게 샘플링 될 텐데요, 이 같은 결과를 얻기 위해 메트로폴리스와-헤이스팅스가 고안한 알고리듬의 절차는 다음과 같습니다.
(0) 타겟으로 하는 분포 $p(x)$에 대해서 $p(x)$와 비례하는 $f(x)$를 정의한다. $f(x)$는 계산하기 쉬울 수록 더 좋다.
(1) 초기값 $x0$를 선택한다. 특별한 이유가 없다면 임의의 값을 사용한다.
(2) 아래 (2-1) ~ (2-4) 절차를 계속 반복한다. n=0 에서 시작한다.
(2-1) $x'$를 선택한다. 이 값은 임의로 선택된 값이거나, $x_n$과 관련된 값이어도 된다.
(2-2) $\alpha = \frac{f(x')}{f(x_n)}$를 계산한다. 이 $\alpha$값은 $\frac{p(x')}{p(x_n)}$과 같다.
(2-3) $[0, 1]$ 범위의 임의의 값 $u$를 생성한다.
(2-4) 만일, $u<\alpha$ 이면, $x_{n+1} = x'$ 가 되고, 그렇지 않으면 $x_{n+1} = x_n$ 이 된다.
위 (2)의 과정을 $\{x_n | i=1, 2, 3, ... \}$ 의 분포가 수렴할 때 까지 반복한다.
(2)를 계속 반복하여 수렴된 분포 $\{x_n | i=1, 2, 3, ... \}$를 얻었다면, 이 분포는 $p(x)$를 따르게 됩니다.
(2-2)에서 구해야 하는 값 $\alpha$는 $\frac{p(x')}{p(x_n)}$ 인데, $f(x)$가 $p(x)$와 비례한다는 사실로 부터 $\frac{p(x')}{p(x_n)}$ 대신, 더 계산하기 쉬운 $\frac{f(x')}{f(x_n)}$를 계산하였습니다. 지금처럼 꼭 $f(x)$를 이용한 계산이 아니더라도, 결과적으로 $\frac{p(x')}{p(x_n)}$를 구할 수 있는 방법이 있다면 그 방법을 사용하면 됩니다. 기각 샘플링을 이용하여 적분을 하기 위해서는 $p(x)$의 최대값이 얼마인지 알아야 하지만 (정확히는 최대값의 상계를 알아야 하지만), 메트로폴리스-헤이스팅스 샘플링을 이용하면 $p(x)$의 절대값은 알 필요가 없다는 장점이 있습니다.
(2-4)에서 $x_n$ 혹은 $x'$ 중 하나가 $x_{n+1}$이 되는데, $p(x') > p(x_n)$ 이라면 무조건 $x'$가 선택이 되고, $p(x')<p(x_n)$이라고 하더라도, $\frac{p(x')}{p(x_n)}$값의 크기에 따라서 확률이 더 낮은 $x'$가 선택 될 수도 있습니다. 이 점이 매우 흥미롭습니다. $x_n, x'$ 중에서 확률이 더 높은 점이 무조건 $x_{n+1}$이 된다면 수열 $x_n$는 확률이 가장 높은 점, 즉 $p(x)$의 최대값이 수렴하여 디락 델다 분포와 같은 결과를 얻겠지만, $x'$의 확률이 $x_n$의 확률 보다 더 낮더라도 $x'$이 $x_{n+1}$로 선택될 확률이 있기 때문에, 결과적으로 $p(x)$의 분포를 얻을 수 있습니다.
메트로폴리스-헤이스팅스 알고리듬 구현하여 실행하기
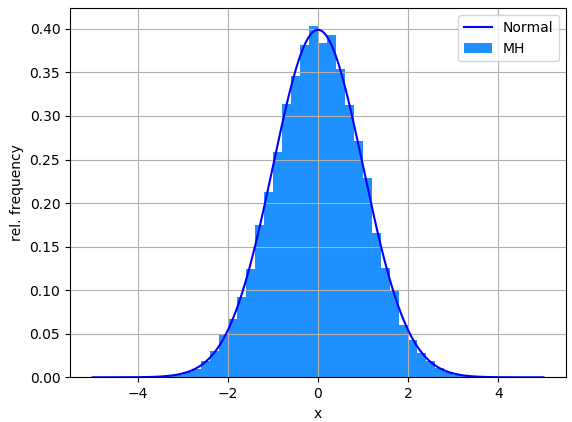
위에서 설명한 메트로폴리스-헤이스팅스 알고리듬은 파이썬 프로그램으로 구현하여 얻은 분포입니다. 히스토그램으로 표현한 것이 시뮬레이션으로 부터 얻은 $\{x_n | i=1, 2, 3, ... K\}$의 빈도를 나타낸 것이고, 파란색 선은 $N(x)$를 나타냅니다. 총 반복횟수 $K$는 $10^5$번 입니다. 히스토그램과 해석적인 커브가 거의 일치함을 확인할 수 있습니다.
https://www.youtube.com/watch?v=CBWih7YFgD8
위 과정을 영상으로 보면 위와 같습니다. 초기에는 특정한 값을 중심으로 샘플링이 되지만, 시행 횟수가 증가할 수 록, 원하는 분포인 정규 분포와 일치하는 분포를 얻어 갑니다.
$N(x)$를 따르는 $10^5$개의 값이 있으니, 이를 이용하여 $\Big\langle x^2 \Big \rangle _{N(x)}$ 를 구하면 되는데요, 이는 단순히
$$A = \frac{1}{K} \sum_{n=1}^{K} x_n^2$$
입니다. 실제로 계산을 하면 그 값은 $A = 1.0093$을 얻습니다.
닭 잡는데 소 잡는 칼을 쓴 겪이지만, 소를 잡기 위해서는 이 칼이 필요하다.
$K = 10^5$ 번의 반복(즉, 샘플링)을 통해서 얻는 결과 치고는 위 결과($A = 1.0093$)은 그리 만족할 만한 결과는 아닙니다. 구분구적법과 같이 직관적이면서도 무작위성에 의존하지 않는 방법으로 계산을 하면 더 적은 계산량으로 부터 더 정확한 결과를 얻을 수 있을 것 입니다. 또는 기각 샘플링을 통해서 얻는 결과가 메트로폴리스-헤이스팅스 알고리듬을 통해 얻은 샘플링으로 부터 얻은 결과보다 더 정확할 수 도 있고요. 괜히 더 노력은 했지만, 결과는 안 좋아진 것 같은 기분입니다.
맞습니다. 간단한 적분, 특히 입력 변수의 공간 차원이 저 차원이거나 피적분함수 계산에 들어가는 계산량이 크지 않다면 메트로폴리스-헤이스팅스 샘플링 사용한 몬테 카를로 적분은 비효율적인 적분 방법입니다. 그러나! 입력 변수의 공간이 매우 커지거나 피적분 함수이 계산이 힘든 적분일수록 메트로폴리스-헤이스팅스 샘플링에 기반한 몬테 카를로 적분은 그 위력을 발휘 합니다. 다음 포스팅을 통해서 차차 예시를 통해 몬테 카를로 적분의 위력을 알아 보도록 하겠습니다.
'수학' 카테고리의 다른 글
| 유한요소법(Finite Element Method)으로 미분 방정식(헬름홀츠 방정식) 풀기 (0) | 2021.08.19 |
|---|---|
| 2차원 헬름홀츠 방정식(Helmholtz equation) 풀기 : 고유 함수의 개형, 고유 진동수 및 고유 진동수의 분포 (1) | 2021.08.16 |
| 파이썬을 이용한 몬테 카를로 적분(Monte Carlo Integration) 구현 (2) | 2021.08.14 |
| 몬테 카를로 시뮬레이션(Monte Carlo Simulation) 의 이해 : 원주율값 구하기 (+파이썬 시뮬레이션 코드) (5) | 2021.08.12 |
| [선형대수-3, 고전역학-1] 행렬대각화를 이용한 결합진동자(coupled oscillator)의 운동방정식의 쉬운 풀이 (0) | 2021.01.09 |



