https://studyingrabbit.tistory.com/56
슈뢰딩거 방정식을 수치 해법으로 풀기 (1): 슈팅 방법으로 알아보는 고유값 문제, 무한 포텐셜
지난 세 번의 포스팅을 통해 미분 방정식을 수치 해법으로 푸는 과정을 알아봤습니다. 수치 해법으로 미분 방정식을 푸는것에 대해서 잘 모르신다면, 아래 포스팅을 먼저 보고 나서 이 포스팅을
studyingrabbit.tistory.com
지난 포스팅에서 수치 해법으로 슈뢰딩거 방정식을 풀어 보았습니다. (지난 포스팅을 읽지 않으신 분은 위 글 부터 먼저 읽기를 권장합니다) 양자 역학 문제 중, 가장 간단한 문제인 무한 우물 문제에 슈팅 방법을 적용하여 고유값과 고유 함수를 구했습니다. 수치 해법으로 구한 값은 해석적으로 구한 값과 매우 일치하였습니다.
단조화 진동자 문제
이번 포스팅에서는 그 다음 문제를 풀어 보겠는데요, 무한 우물 다음 문제는 단조화 진동자 문제 입니다. 단조화 진동자 문제란 입자가 포텐셜 $$V(x) = \frac{1}{2}x^2$$ 필드에 놓여 있을 때의 문제로 양자 역학 뿐 아니라, 물리의 모든 영역에 있어서 가장 중요한 문제입니다. 단조화 진동자의 슈뢰딩거 방정식은 (편의상 물리 상수는 모두 1로 취급 하였습니다)
$$-\frac{1}{2}\psi''(x) + \frac{1}{2}x^2 \psi(x) = E\psi(x)$$
이고 경계 조건은
$$\psi(x \rightarrow \pm \infty) = 0$$
입니다.
지난 포스팅에서 이미 언급하였는데, 포텐셜이 $V(x \rightarrow \pm \infty) = 0$ 을 만족하는 경우, 파동 함수의 경계 조건은 위의 경우와 같이 $\psi(x \rightarrow \pm \infty) = 0$가 됩니다. 수치 해법에서 무한대를 다루기란 매우 어려우니, 실제적으로 가정하는 파동 함수의 경계 조건은, 충분히 큰 $L$에 대해서 $\psi(x = \pm L) = 0$ 로 놓을 수 있습니다. 따라서 우리가 수치 해법으로 풀어야 하는 방정식의 형태는
$$\psi''(x) = 2 \Big (\frac{1}{2}x^2 - E \Big) \psi(x)$$
$$\psi( \pm L) = 0$$
입니다.
대칭성
문제를 그냥 곧이 곧대로 풀어도 되지만, 주어진 문제의 대칭성을 이용한다면 좀 더 우아하게 풀 수 있습니다. 단조화 진동자의 포텐셜은 변환 $P(x) : x \rightarrow -x$ 에 대해서 불변입니다. 그리고 해밀토니안 역시 $P(x)$에 대해서 불변입니다. 익숙한 표현법으로 표현하자면, $[H, P] = 0$ 입니다. 따라서 파동 함수 역시 변환 $P(x)$에 대해서 고유 함수이어야 하고, 이로 부터 해밀토니안의 고유 함수는 우함수($y$축 대칭 함수) 혹은 기함수(원점 대칭함수)가 됩니다.이 내용은 양자 역학 교과서에 꼭 나오는 내용입니다. 수치 해법을 이용하여 문제를 풀 때도 대칭성을 이용하면 계산을 깔끔하고 효율적으로 할 수 있습니다.
파동 함수가 우함수일 경우, 파동 함수의 $x=0$에서의 미분값은 반드시 $0$이어야 합니다. 그리고 $x$의 모든 영역에서 문제를 풀 필요가 없고 단지 $x \gt 0$ 영역에서만 풀면 $\psi(-x) = \psi(x)$ 성질을 이용하여 $x \lt 0$ 영역의 파동 함수도 구할 수 있습니다. 파동 함수가 기함수일 경우, 파동 함수의 $x=0$에서의 값은 반드시 0이어야 합니다. 또 위와 같은 이유로 $x \gt 0$ 영역에서만 문제를 풀면 됩니다.
위 논의로 부터 우함수 해를 구하는 경우 경계 조건은 $\psi(0) = 1, \psi'(0)=0$ 으로 놓을 수 있고, $x \gt 0$ 영역의 문제만 풀면 됩니다. 기함수 해를 구하는 경우 경계 조건은 $\psi(0) = 0, \psi'(0)=1$ 이 됩니다. 각 경우에 함수값과 미분값을 $1$로 두었는데, 지난 포스팅에서 설명한 바와 같이 슈뢰딩거 방정식은 선형 방정식 이기 때문에 $1$이 아닌 임의의 $0$이 아닌 실수로 두어도 됩니다. 편의상 $1$로 가정한 것 입니다. 최종적으로 정규화 된 (Normalized) 파동 함수를 구하게 된다면, 결과는 모두 동일합니다.
파동 함수가 우함수일 경우 문제 풀기

$E = 0.45, 0.5, 0.55$ 에 대한 수치 해법으로 얻은 해를 그리면 위와 같습니다. 위 과정에서 $L=5$로 두었습니다. 따라서 서로 다른 $E$에 대한 파동 함수를 얻고, 이 파동 함수가 $\psi_E(L) = 0$을 만족하는 $E$가 문제의 고유값이 됩니다. 위 그래프에서 볼 수 있듯, $E=0.5$ 인 경우, 파동 함수가 $x=L=5$에서 $0$으로 수렴하게 됨을 볼 수 있고, 따라서 $E = 0.5$가 고유 함수가 되고 파란색으로 표시한 $\psi_{E = 0.5}(x)$가 이에 대응하는 고유 함수가 됩니다. 단조화 진동자 문제에서 $E_0 = 1/2$이 된다는 것은 다 아실텐데, 수치 해법으로 푼 결과가 해석적인 결과와 일치함을 확인할 수 있습니다.
고유값이 아닌 $E$에 해당하는 방정식의 해도 물론 계산을 통해 구할 수 있습니다. 이 해를 그리면 녹색(고유값 보다 조금 더 작은 $E$에 해당하는 경우) 혹은 붉은색(고유값 보다 조금 더 큰 $E$에 해당하는 경우) 형태의 함수가 됩니다. 이 함수는 당연히 경계 조건을 만족하지 못 하는데, 단순히 경계 조건을 만족하지 못 할 뿐 아니라, 경계치$(x=\pm L)$ 근처에서 함수값이 음 혹은 양의 무한대로 발산하게 됨을 확인 할 수 있습니다. 즉, 수학적으로는 임의의 $E$에 대해서 슈뢰딩거 방정식을 만족하는 함수 $\psi(x)$를 구할 수 있으나, 이 $\psi(x)$는 경계 조건을 만족하지 못할 뿐 아니라, 발산하게 된다는 결론을 내릴 수 있습니다.
양자 역학의 수학적 공리 중에 "파동 함수는 힐베르트 공간(Hilbert Space)의 원소이다" 라는 조건이 있습니다. 파동 함수가 힐베르트 공간의 원소가 되려면, 파동 함수가 정의되는 전 공간에서 파동 함수의 절대값의 제곱의 적분이 유한한 값을 가져야 합니다. 이 문제에 적용한다면 $\int_{-L}^{L} \Big|\psi(x) \Big|^2dx \lt \infty$ 입니다. 그런데, 고유값이 아닌 $E$에 대응되는 함수는 무한대로 발산하기 때문에 $\int_{-L}^{L} \Big|\psi(x) \Big|^2dx 적분이 정의 되지 못하고, 따라서 힐베르트 공간의 원소가 될 수 없습니다. 다시 한 번 정리하면, 순수하게 수학적으로는 슈뢰딩거 방정식의 해가 될 수 있겠지만, 그 해는 물리적인 의미를 갖지 못 하게 됩니다. 이 같은 현상은 단조화 진동자 문제에 국한된 것이 아니라, 일반적인 포텐셜에서의 슈뢰딩거 방정식에 적용 되는 현상입니다.
$E$ vs $\psi_E(x=L)$
다른 고유값을 구하기 위해서 $E$ vs $\psi_E(x=L)$ 그래프를 그려 보도록 하겠습니다. 지난 포스팅에서 설명한 바와 같이 이 그래프와 $E$축과의 교점에 해당하는 $E$가 고유값이 됩니다.

$E \le 1/2$ 인 경우, $\psi_E(x=L)$ 가 무지막지 하게 큰 값을 갖습니다. 물론 고유값이 아닌 임의의 $E$에서 역시 이 값이 발산해야 하기 때문에 매우 큰 값을 가져야 하지만, $x=L$와 같이 $x$의 영역을 제한 했기 때문에 무한한 값을 나오지 않고 적당히 큰 값이 나오게 됩니다. 이 스케일로 그래프를 그리면 $E \gt 2$ 영역은 거의 알아 볼 수 없기 때문에, $y$축의 스케일을 좀 조정하여 다시 그리면,
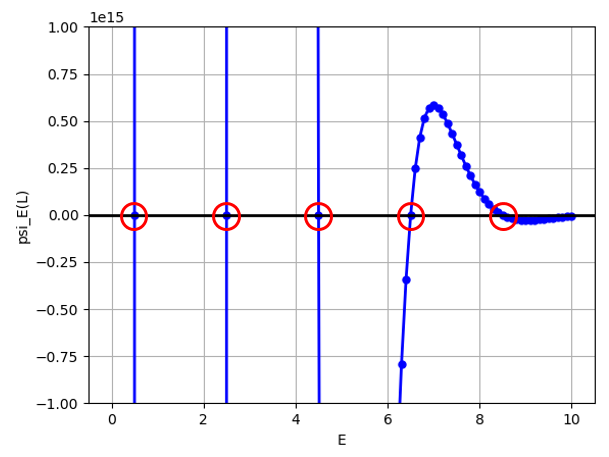
이 됩니다. 붉은 원으로 표시한 점이 그래프와 $E$축이 만나는 값이며, 이 값은
$$E = 0.5, 2.5, 4.5, 6.5, 8.5$$
가 됩니다. 해석적인 고유값 $E_n = (n+\frac{1}{2})$에서 $n$이 짝수인 경우의 고유값에 해당 합니다.

$E = 1/2, 2 + 1/2, 4 + 1/2$에 해당하는 고유 함수의 개형은 위와 같습니다. 정규화 되지 않은 함수 입니다.
파동 함수가 기함수일 경우 문제 풀기
기함수의 파동 함수를 찾을 때는 $x=0$에서의 경계 조건만 바꾸면 됩니다. 위와 같은 방식으로 계산을 하면, $E = 1 + 1/2, 3 + 1/2, 5 + 1/2$에 해당 하는 파동 함수가 경계 조건을 만족 시키면서 발산하지 않음을 확인할 수 있습니다. 이에 대응되는 파동 함수를 그리면 아래 그래프와 같습니다.

위의 과정과 같이 단조화 진동자의 고유값과 고유 함수를 모두 구해 봤습니다. 물론 에너지 값이 크지 않은 바닥 상태와 초기 여기 상태를 구한 것 입니다. 보다 높은 여기 상태의 해를 구하기 위해서는 $E$를 더 큰 범위에서 계산을 하면 됩니다. 지난 포스팅에서 설명한 바 있는 이분법(bisection method)를 사용하여 정확하고 빠르게 고유 상태를 얻을 수 있습니다.
단, 고유 에너지의 값이 커지면 파동 함수가 퍼저 있는 $x$의 영역이 더 커지게 됩니다. 바로 위 두 그래프에서도 이를 확인 할 수 있는데, 고유값이 큰 파동 함수 일수록 $x^2$의 기대값 $\langle \psi | x^2 | \psi \rangle$이 커집니다. 따라서 우리가 잡은 인위적인 경계값 $L$이 더 커져야 정확한 계산이 됩니다. 즉 $ \langle \psi | x^2 | \psi \rangle \ll L$ 이 되는 $L$을 잡아야 $L = \infty$와 같은 효과를 얻을 수 있습니다.
$x^4$에 비례하는 포텐셜 문제
재미삼아 $x^4$에 비례하는 포텐셜의 슈뢰딩거 방정식을 풀어 보도록 하겠습니다. 보통은 $x^4$에 해당하는 포텐셜을 단조화 진동자의 포텐셜에 섭동 항으로 추가하여 섭동 이론으로 풀곤 하는데요, 그렇게 하면 정성적인 변화 보다는 단지 약간의 정량적인 변화만 있기 때문에, 별로 재미가 없습니다. 따라서 그냥 $V(x) = \frac{1}{4} \cdot 0.1 \cdot x^4$의 문제를 풀어 보도록 하겠습니다. 여기서 추가적으로 $0.1$을 곱한것은 $x \in [-5, 5]$의 범위에서 최대한 $\frac{1}{2}x^2$와 유사한 크기의 포텐셜을 만들기 위함 입니다. 두 포텐셜을 비교하면,

와 같습니다. $x^2$ 포텐셜에 비해서 $x^4$ 포텐셜은 $x=0$ 근처에서는 더 완만하지만 $x=5$ 근처에서는 더 가파르게 증가합니다. $x^4$ 포텐셜 역시 좌우 대칭이기 때문에, 위에서 사용했던 우함수/기함수의 대칭성을 그대로 이용할 수 있습니다.

$E$ vs $\psi_E(x=L)$ 그래프는 위와 같습니다. 위 그래프를 $\psi_E(x=L) = 0$ 근처를 확대하면,

이 그래프와 같고, 붉은색으로 동그라미 친 에너지 값이 고유값에 해당됩니다. 이분법(bisection method)로 정확하게 고유값을 구하면,
$$E = 0.1953, 1.3734, 2.9955, 4.8869, 6.9885, 9.2787$$
을 얻습니다. 해석적인 방법으로 위 문제를 어떻게 푸는지 모르겠어서, 해석적인 값과 비교는 불가능하지만, 우리가 틀리지지 않게 프로그래밍을 했다는 것을 단조화 진동자 문제를 통해서 확인했기 때문에, 이 값이 참값과 매우 가까울 것 입니다.

위 고유값에 대응되는 고유 함수는 위 그래프와 같이 생겼습니다. 단조화 진동자의 경우와 포텐셜이 정성적으로는 거의 같기 때문에, 고유 함수 역시 정성적으로는 비슷하게 생겼습니다. 그러나 기저 상태의 고유 함수가 단조화 진동자의 기저 상태의 고유 함수에 비해 좀 더 퍼져 있습니다. $x^4$의 위치 에너지가 원점 근처에서 좀 더 평평하기(soft) 때문입니다. 위와 같은 방식으로 기함수 조건의 문제를 풀 수 있지만, 생략 하도록 하겠습니다.
이번 포스팅의 요약
어떻게 생각하면, 이번 포스팅은 지난 포스팅에서 포텐셜을 $0 \rightarrow \frac{1}{2}x^2$으로 바꾼 것 밖에 없다고 생각할 수 도 있습니다. 사실... 수학적으로만 생각한다면 그것이 맞습니다. 하지만 물리적으로 생각할 때 몇 가지의 새로운 내용이 있었는데,
(1) 시스템(해밀토니안 혹은 포텐셜)의 대칭성을 이용하여 문제는 효율적으로 풀었다.
(2) 고유값이 아닌 $E$값에 대응되는 슈뢰딩거 방정식의 해의 개형은 어떠한 특징을 갖는지 확인하였다. 이 경우 해는 당연히 경계 조건을 만족하지 못하고 더불어 무한히 발산한다. $\int_{-L}^{L} \Big|\psi(x) \Big|^2dx 값이 정의 되지 않는다. 이는 매우 일반적인 현상이다.
입니다.
학부 수준의 양자 역학 시간에는 (거의 항상) 해석적으로 풀이가 가능한 문제만을 다룹니다. 무한 포텐셜 우물, 단조화 진동자, 수소 원자와 같은 문제입니다. 양자 역학에 대한 중요한 개념을 배우기도 바쁘기 때문에 쉬우면서도 해석적으로 풀리는 문제에 집중하는 것이 당연합니다. 하지만, 매우 소수의 문제를 제외하고는 일반적인 문제는 해석적으로 풀리지 않습니다. 따라서, 일반적인 문제를 풀 때는 반드시 수치 해법이 적용 될 수 밖에 없습니다. 뿐만아니라, 해석적으로 풀리는 문제라고 하더라도 수치 해법으로 문제를 푸는 과정과 결과를 알아 두면 일반적인 양자 역학의 문제를 이해하거나 양자 역학의 특징을 이해하는데 큰 도움이 됩니다.
'물리학' 카테고리의 다른 글
| 1차원 공간에서 슈뢰딩거 방정식에 대한 몇 가지 정리 (0) | 2021.10.30 |
|---|---|
| 몬테 카를로 시뮬레이션을 이용하여 통계 역학의 문제 풀기 (1) : 토이 모델 예시 (0) | 2021.10.24 |
| 슈뢰딩거 방정식을 수치 해법으로 풀기 (1): 슈팅 방법으로 알아보는 고유값 문제, 무한 포텐셜 우물 문제 풀기 (0) | 2021.10.16 |
| 룽게-쿠타 방법(Runge-Kutta method) 을 활용하여 보다 빠르고 정확하게 미분 방정식 문제를 수치 해법으로 풀기 + 파이썬 코드 (0) | 2021.10.15 |
| 수치 미분 방정식 풀이법을 이용하여 최종값 조건이 주어진 문제 풀기 : 슈팅 방법 (0) | 2021.10.15 |


