해밀턴-야코비 방정식 복습
해밀턴-야코비 방정식을 고전 역학 문제를 푸는 또 다른 방법론에 의해 도입된 방정식 입니다. 이 방법에서는 일반화 좌표와 운동량을 직접적인 미분 방정식을 통해서 구하지 않고, 시스템에 적합한 정준 변환을 찾고, 이 정준 변환으로 부터 일반화 좌표와 운동량의 시간에 따른 함수를 구합니다. 해밀턴-야코비 방정식은 이 적합한 정분 변환을 구하는 방식입니다. 해밀턴-야코비 방정식은 정준 변환의 생성자 $F$ 가 만족해야 하는 편미분 방정식으로
$$H\Big(q, \frac{\partial F}{\partial q}, t \Big) + \frac{\partial F}{\partial t} = 0$$
입니다.
이차원 단조화진동자 문제를 라그랑주 방정식과 해밀턴-야코비 방정식을 이용해 풀기
해밀턴-야코비 방정식의 유도 과정만 보면, 어떻게 고전 역학의 문제를 실제로 풀 수 있을지에 대한 감이 잘 잡히지 않습니다. 지난 포스팅에서는 1차운 단조화진동자의 예시를 들었는데, 이번에는 조금 복잡한 2차원 단조화진동자의 예시를 들어 보도록 하겠습니다. 단순히 해밀턴-야코비 방정식으로만 풀기보다는 일단 라그랑주 방정식을 통해서 문제를 푼 다음, 해밀턴-야코비 방정식으로 푸는 것과 비교를 해 보도록 하겠습니다.
(편의상 질량, 용수철 상수는 모두 1로 놓겠습니다) 이 시스템의 라그랑지안은
$$L(x, y, \dot{x}, \dot{y}) = \frac{1}{2}\dot{x}^2 + \frac{1}{2}\dot{y}^2 - \frac{1}{2}x^2 - \frac{1}{2}x^2$$
입니다. 오일러-라그랑주 방정식 $\frac{d}{dt}\Big(\frac{\partial L}{\partial \dot{q}} \Big) - \frac{\partial L}{\partial q} = 0$에 위 라그랑지안을 대입하고 정리하면,
$$\ddot{x} = -x$$
$$\ddot{y} = -y$$
와 같은 각 일반화 좌표 마다 일반화 좌표를 시간에 대한 2계 미분한 항이 있는 연립 미분 방정식이 얻어집니다. 위 시스템은 $x$와 $y$의 움직임이 서로 독립적이기 때문에 $x$에 대한 식에는 $x$만, $y$에 대한 식에는 $y$만 있고, 연립 미분 방정식이라기 보다는 완전히 별개인 독립된 두 개의 미분 방정식이 얻어집니다. 위 미분 방정식의 해는 $x(t) = A \cos t + B \sin t$, $y(t) = C \cos t + D \sin t$ 로 주어진다는 것을 쉽게 알 수 있습니다. $A, B, C, D$ 값은 초기 조건에 의해서 결정 됩니다.
라그랑주 방정식에 대해서 알고 있다면, 개개의 역학 문제는 라그랑주 방정식을 통해서 푸는 것이 가장 쉽다는 것을 아마 알고 있을 것이고, 위와 같은 기계적인 방법에 따라서 최종 미분 방정식을 풀면 됩니다. 매우 익숙한 방법입니다.
이 문제를 이제는 해밀턴-야코비 방정식을 통해서 풀어 보도록 하겠습니다. 해밀턴-야코비 방정식의 풀이는 역시나 시스템의 해밀토니안을 쓰는 것 부터 시작되는데, 시스템의 해밀토니안은
$$H(x, y, p_x, p_y) = \frac{1}{2}p_x^2 + \frac{1}{2}p_y^2 + \frac{1}{2}x^2 + \frac{1}{2}y^2$$
입니다. 생성자 함수를 $F$가 아닌, 이제 부터는 $S$라고 쓰면 (보통 $S$라고 쓰는 것이 일반적입니다), 이 시스템의 해밀턴-야코비 방정식은
$$\frac{1}{2}\Big(\frac{\partial S}{\partial x} \Big)^2 + \frac{1}{2} \Big( \frac{\partial S}{\partial y} \Big)^2 + \frac{1}{2}x^2 + \frac{1}{2}y^2 + \frac{\partial S}{\partial t} = 0$$
이 됩니다. 이 시스템은 시간에 대해 무관한 시스템으로, $S = W - \alpha t$와 같이 가정할 수 있고, 또한 $x$와 $y$가 서로 무관한 시스템이기 때문에 $S = W_x(x, \alpha_x) + W_y(y, \alpha_y) - \alpha_x t -\alpha_y t$ 처럼 $x$에 대한 항과 $y$에 대한 항으로 나누어 쓸 수 있습니다. 이 $S$를 위 식에 대입하면,
$$\frac{1}{2} \Big( \frac{\partial W_x}{\partial x}\Big)^2 + \frac{1}{2} x^2 = \alpha_x$$
$$\frac{1}{2} \Big( \frac{\partial W_y}{\partial y}\Big)^2 + \frac{1}{2} y^2 = \alpha_y$$
를 얻습니다. 이 식의 해법은 지난 포스팅에서 이미 설명하였습니다. $x(t), y(t), p_x(t), p_y(t)$에 대한 최종식은
$$x(t) = \sqrt{2 \alpha_x} \sin (t + \beta_x)$$
$$y(t) = \sqrt{2 \alpha_y} \sin (t + \beta_y)$$
$$p_x(t) = \sqrt{2 \alpha_x} \cos (t + \beta_x)$$
$$p_y(t) = \sqrt{2 \alpha_y} \cos (t + \beta_y)$$
가 됩니다. 여기서 상수 $\alpha_x, \alpha_y, \beta_x, \beta_y$는 초기조건에 이해 결정되는 값으로, $\alpha$는 각 자유도에서의 역학적 에너지, $\beta$는 각 자유도에서의 위치와 운동량의 값의 비율(위상)과 관련된 값입니다.
차이가 느껴지시나요?
라그랑주 방정식에서 최종적으로 풀어야 하는 수학 문제는
$$\frac{d^2 x}{dt^2} = -x$$
와 같이 일반화 좌표 $x$를 시간에 대해 2번 미분한 항이 들어 있는 미분 방정식이고, 해밀턴-야코비 방적시에서 최종적으로 풀어야 하는 수학 문제는
$$\frac{1}{2} \Big( \frac{\partial W_x}{\partial x}\Big)^2 + \frac{1}{2} x^2 = \alpha_x$$
와 같이 일반화 좌표의 함수인 해밀턴 특성함수(Characteristic function) $W(x)$를 일반화좌표 $x$로 한 번 미분한 미분 방정식 입니다. 이 두 방법은 완전히 풀이법이 다른데, 정리하면,
| 라그랑주 방정식 | 해밀턴-야코비 방정식 | |
| 독립 변수 | $t$ | $x$ |
| 종속 변수 | $x =x(t)$ | $W = W(x)$ |
| 미분식 | $\frac{d^2 x}{dt^2}$ | $\frac{\partial W}{\partial x}$ |
| 초기 조건 (적분 상수) | 방정식에는 나타나지 않음, $x(t)$ 식에 포함 돼 있음 | 방정식에 나타남, $W(x, \alpha)$식에 포함 돼 있음 |
와 같습니다. 동일한 대상에 대해서 답을 구하는 두 방법론(체계)가 이렇게 까지 다르다는 것도 무척이나 신기합니다.
라그랑주 방정식에서 얻은 해 $x(t)$ 를 그래프로 표현하면,
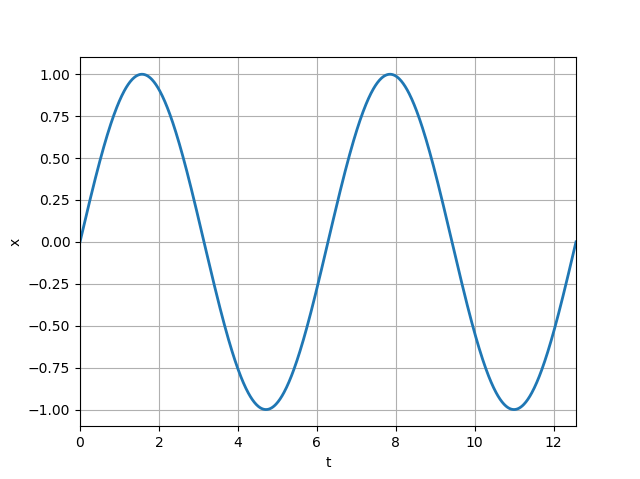
와 같고, 해밀턴-야코비 방정식에서 얻은 해 $W(x)$를 그래프로 표현하면,

와 같습니다. 다시 한 번 설명하지만, 라그랑주 방정식을 통해서는 시간에 따른 일반화 좌표의 함수 $q(t)$를 직접적으로 얻는 것이고, 해밀턴-야코비 방정식을 통해서는 해밀턴 특성함수 $W(q)$를 얻습니다. 해밀턴 특성함수와 이 해밀턴 특수함수를 생성자로 하는 정준 변환으로 부터 $q(t), p(t)$를 최종적으로 얻습니다.
위 문제를 극좌표를 이용해서 풀면 조금 더 재미(?) 있다
라그랑지안을 극좌표로 나타내면 $L(r, \theta) = \frac{1}{2}\dot{r}^2 + \frac{1}{2}r^2 \dot{\theta}^2 - \frac{1}{2}r^2$ 과 같고, 이로 부터 유도되는 오일러-라그랑주 방정식은
$$r : \ddot{r} = -r + 2r \dot{\theta}^2$$
$$\theta : r^2 \dot{\theta} = l \text{ constant}$$
입니다. $\theta$에 대한 식을 이용하여 $r$에 대한 식에서 $\theta$를 소거하면 (라그랑지안의 극좌표 표현에서는 두 일반화 좌표 $r, \theta$의 교차항이 있기 때문에, 연립 미분 방정식을 풀어야 합니다),
$$\ddot{r} = -r + 2 \frac{l^2}{r^3}$$
의 최종 미분 방정식을 얻습니다. 여기서 $r(t)$를 얻으면 이 값을 $\theta$에 대한 식에 대입하여 $\theta(t)$를 얻습니다. 실제로 위 미분 방정식을 푸는 것은 조금 귀찮기 때문에 생략합니다.
해밀토니안을 극좌표로 나타내면 $H(r, \theta, p_r, p_{\theta}) = \frac{1}{2}p_r^2 + \frac{1}{2}\frac{p_{\theta}^2}{r^2} + \frac{1}{2}r^2$과 같습니다. 이 해밀토니안은 $\theta$와 무관하기 때문에, $S = W_r(r, \alpha_r) + W_{\theta}(\theta, \alpha_{\theta}) - \alpha t = W_r(r, \alpha_r) + \theta \alpha_{\theta} - \alpha t$ 의 형태로 가정할 수 있고, 이를 해밀턴-야코비 방정식에 대입하면,
$$\frac{1}{2}\Big( \frac{\partial W_r}{\partial r}\Big)^2 + \frac{\alpha_{\theta}^2}{2r^2} + \frac{1}{2}r^2 = \alpha$$
가 됩니다. 역시나 실제로 이 미분 방정식을 푸는 것은 조금 귀찮기 때문에 생략합니다.
두 방법에서 최종적으로 풀어야하는 (사실 귀찮아서 풀지 않고 풀이를 생략했던) 최종 미분 방정식은 각각
$$\text{Euler-Lagrange equation : } \frac{d^2}{dt^2}r(t) = -r(t) + 2 \frac{l^2}{r(t)^3}$$
$$\text{Hamilton-Jacobi equation : } \frac{1}{2}\Big( \frac{\partial}{\partial r}W(r, \alpha)\Big)^2 + \frac{\alpha_{\theta}^2}{2r^2} + \frac{1}{2}r^2 = \alpha$$
로 판이하게 다르게 생겼습니다. 오일러-라그랑주 방정식에서는 $r(t)$를 구하는게 목표이고, 해밀턴-야코비 방정식에서는 $W(r, \alpha)$를 구하는것이 목표입니다. 고전 역학에 대해서 전혀 배경 지식이 없는 사람이 저 두 방정식을 봤다면, 이 두 방정식이 공히 2차원 단조화진동자를 기술하는 방정식이라고는 전혀 생각하지 못 할 것 입니다.
개별 문제를 푸는데는 역시 라그랑주 방정식을 푸는게 더 쉽다
해밀턴 역학, 정준 변환, 생성자, 해밀턴-야코비 방정식과 같은 추가적인 개념과 방법론에 대해서 공부를 한 참 하고나서 문제를 풀었는데, 해밀턴-야코비 방정식을 통해서 개별 문제를 푸는 것은 라그랑주 방정식을 통해서 문제를 푸는 것에 비해서 훨씬 더 복잡하고 어렵습니다. (사실은, 절대적으로 더 어렵다기 보다는 라그랑주 방정식과 같이 최종적으로 구하려고 하는 일반화 좌표 함수에 대한 방정식이 더 익숙하다고 할 수 있습니다)
사실, 개별 역학 문제를 푸는데 있어서 라그랑주 방정식을 푸는 것 만큼 쉬운 방법은 없습니다. 뉴턴 방정식 $\vec{F} = m\vec{a}$를 이용하여 풀기 위해서는 각 물체에 작용하는 힘의 크기와 방향을 모두 알아야 하는데, 이게 그리 쉽지 않습니다. 또한 복잡한 구속조건이 있는 경우엔 그 난이도가 급격히 상승합니다. 해밀턴 방정식을 이용하여 풀면, 그냥 풀어도 될 정도의 간단한 문제인데, 이걸 더 간단히 하겠다고 들이는 노력이 아깝습니다. 해밀턴-야코비 방정식을 이용하여 풀면, 실제 문제 해결과는 상관이 없는 매우 어려운 문제를 어렵게 풀었을 뿐 그게 답이라는 느낌은 나지 않습니다.
해밀턴 역학은 고전 역학이라는 큰 시스템을 이해하는데 도움을 주는 방법
해밀턴 역학에 대해서 소개하는 포스팅에서도 언급을 한 것 같은데, 해밀턴 역학, 그리고 이와 관련된 해밀턴-야코비 방정식 등은 사실 개별 문제를 푸는데는 큰 도움이 되지 못 합니다. 하지만 고전 역학이라는 큰 체계를 이해하고, 새로운 개념을 만들고 이를 이용해서 고전 역학계에 대한 더 큰 이해를 하는데는 해밀턴 역학이나 해밀턴-야코비 방정식은 필수적인 요소 입니다. 해밀턴-야코비 방정식을 이용한 고전 역학의 이해를 매우 일상적인 용어로 옮기면, "각 고전 역학 시스템에는 이 시스템에 적합한 해밀턴 특성 함수라는 시스템의 일반화 좌표에 의존하는 함수(일종의 필드와 같은 개념)이 있고, 초기 조건이 주어지면 해밀턴 특성 함수에 의해서 시간에 따른 일반화 좌표와 운동량이 정해진다" 입니다. 뉴턴 역학은 "힘이 가해지면 물체에 가속도가 생긴다" 라고 할 수 있는데, 뉴턴 방정식이 매우 국소적인 의미라면, 해밀턴-야코비 방정식은 시스템 전체적으로 글로벌 한 느낌을 줍니다.
'물리학' 카테고리의 다른 글
| 학부 물리학 테크트리(feat 내가 공부한 책) (2) | 2021.08.25 |
|---|---|
| 물리 논문 읽기 (1) <The stability of matter>(물질의 안정성) by 엘리엇 리브(Elliot H. Lieb) Ep. 01 : 원자의 안정성 (0) | 2021.08.22 |
| [고전역학-7] 해밀턴 역학 : 해밀턴-야코비 방정식 (1) | 2021.01.22 |
| [고전역학-6] 해밀턴 역학 : 정준 변환의 생성자 (Generator) (0) | 2021.01.19 |
| [고전역학-5] 해밀턴 역학 : 정준 변환 Canonical transformation (3) | 2021.01.17 |

